Loading [MathJax]/jax/output/HTML-CSS/jax.js

如果 $\sqrt{3}$ 和 $-\sqrt{3}$ 是 $( x^{4}+x^{3}-23 x^{2}=3 x+60)$ 的零点，求出该多项式的所有零点。

学术数学 NCERT 10 年级

已知：

$\sqrt{3}$ 和

$-\sqrt{3}$ 是

$( x^{4}+x^{3}-23 x^{2}=3 x+60)$ 的零点。

要求：求出该多项式的所有零点。

解

令

$f( x)=x^4+x^3-23x^2-3x+60$

如题所述，

$\sqrt{3}$ 和

$-\sqrt{3}$ 是该多项式的零点。

$( x-\sqrt{3})$ 和

$(x+\sqrt{3})$ 是

$f( x)$ 的因式。

$( x-\sqrt{3})(x+\sqrt{3})$ 也会是

$f( x)$ 的因式。

用

$( x^2-3)$ 除以

$f( x)$ 。

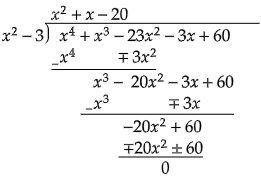
令

$f( x)=0$ 。

$( x^2+x-20)( x^2-3)=0$

$\Rightarrow ( x^2+5x-4x-20)( x^2-3)=0$

$\Rightarrow [ x( x+5)-4( x+5)]( x^2-3)=0$

$\Rightarrow ( x-4)( x+5)( x+3)( x-3)=0$

$\Rightarrow x=4$ 或

$x=-5$ 或

$x=\sqrt{3}$ 或

$x=-\sqrt{3}$

因此，该多项式的所有零点为

$\sqrt{3},\ -\sqrt{3},\ 4$ 和

$-5$ 。

教程点

更新于： 2022-10-10

60 次浏览

开启你的职业生涯

完成课程获得认证

广告