已知多项式$(2x^4 - 9x^3 + 5x^2 + 3x - 1)$的两个零点是$(2+\sqrt{3})$和$(2-\sqrt{3})$，求该多项式的所有零点。

已知：多项式$(2x^4 - 9x^3 + 5x^2 + 3x - 1)$，其中两个零点是$(2+\sqrt{3})$和$(2-\sqrt{3})$。

求解：求该多项式的所有零点。

解

已知$(2+\sqrt{3})$和$(2-\sqrt{3})$是两个零点

$[x - (2+\sqrt{3})][x - (2-\sqrt{3})] = (x - 2 - \sqrt{3})(x - 2 + \sqrt{3})$

$= [(x-2) - \sqrt{3}][(x-2) + \sqrt{3}]$

$= (x-2)^2 - (\sqrt{3})^2$

$= x^2 - 4x + 4 - 3$

$= x^2 - 4x + 1$

$x^2 - 4x + 1$是已知多项式的因式。

用该因式去除已知多项式。

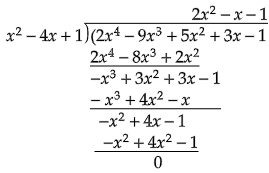
因此，$2x^2 - x - 1$也是已知多项式的因式。

$2x^2 - x - 1 = 2x^2 - 2x + x - 1$

$= 2x(x - 1) + (x - 1)$

$= (x - 1)(2x + 1)$

如果$x - 1 = 0$

$x = 1$

如果$2x + 1 = 0$

$x = -\frac{1}{2}$

因此，已知多项式的另外两个零点是1和$-\frac{1}{2}$。

Tutorialspoint

更新于：2022年10月10日

79次浏览

开启您的职业生涯

完成课程获得认证

开始学习