数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
多项式：多项式是一个表达式，它是变量、常数和指数的组合，其中指数为正整数，通过数学运算组合在一起。例如：$3x^2 -5x + 2$ 是一个多项式，其中，3 - $x^2$ 的系数，$-5$ - $x$ 的系数，2 - 常数，x - 变量。单项式：只有一个项的多项式称为单项式。例如： $3x^4$。二项式：恰好有两个项的多项式称为二项式。例如： $3x^4 + 2xy$。三项式：恰好有三个项的多项式称为三项式。例如： $3x^4 +2xy -3$。
已知：数字为 $\left(\frac{441}{2^{2} .5^{7} .7^{2}}\right)$。要求：确定它是否具有有限或无限小数表示形式。解：由于分母不属于 $2^m×5^n$ 的形式，因此给定的有理数具有无限小数表示形式。
已知：$\alpha$ 和 $\beta$ 是一个多项式的零点。$\alpha+\beta=6$ 且 $\alpha\beta=4$要求：写出该多项式。解：由于它有两个零点，所以它是一个二次多项式。并且它的零点是 $\alpha$ 和 $\beta$。$\Rightarrow ( x-\alpha ) =0\ and\ ( x-\beta ) =0$$\Rightarrow ( x-\alpha )( x-\beta ) =0$$\Rightarrow x^{2} -\alpha x-\beta x+\alpha\beta=0$$\Rightarrow x^{2} -( \alpha+\beta) x+\alpha\beta =0$$\therefore$该多项式为 $x^{2} -( \alpha+\beta) x+\alpha\beta =0$
已知：前 p 项的和 $=ap^{2} +bp$要求：求其公差。解：这里给定的等差数列前 p 项的和为 =$ap^{2} +bp$假设给定等差数列的第一项为 x，公差为 y。那么等差数列的和 $=\frac{p}{2} \ [ 2x+( p-1) y]$$\Rightarrow $ 给定的和 $ap^{2} +bp=\ \frac{p}{2}[ 2x+( p-1) y]$$\Rightarrow 2ap^{2} +2bp=p[ 2x+( p-1) y]$$\Rightarrow 2p( ap+b) =p[ 2x+( p-1) y]$$\Rightarrow 2ap+2b=2x+( p-1) \ y$$\Rightarrow \ \ \ \ \ 2b+2ap=( 2x-y) +\ py$比较两边项$\Rightarrow 2a=y$$2x-y=2b$$\Rightarrow 2x=2b+y$$\Rightarrow 2x=2b+2a$ ... 阅读更多
已知：三角形的两条边的长度分别为 12 厘米和 15 厘米。要求：找到第三条边的长度应该落在什么范围之间。解：三角形应满足以下条件：(i) 任意两边的和大于第三边。(ii) 任意两边的差小于第三边。两边的和 $= 12 + 15 = 27$所以，$27 > 第三边$。两边的差，情况 1：$= 12 - 15 = -3$边的长度应为正数，因此忽略情况 ... 阅读更多
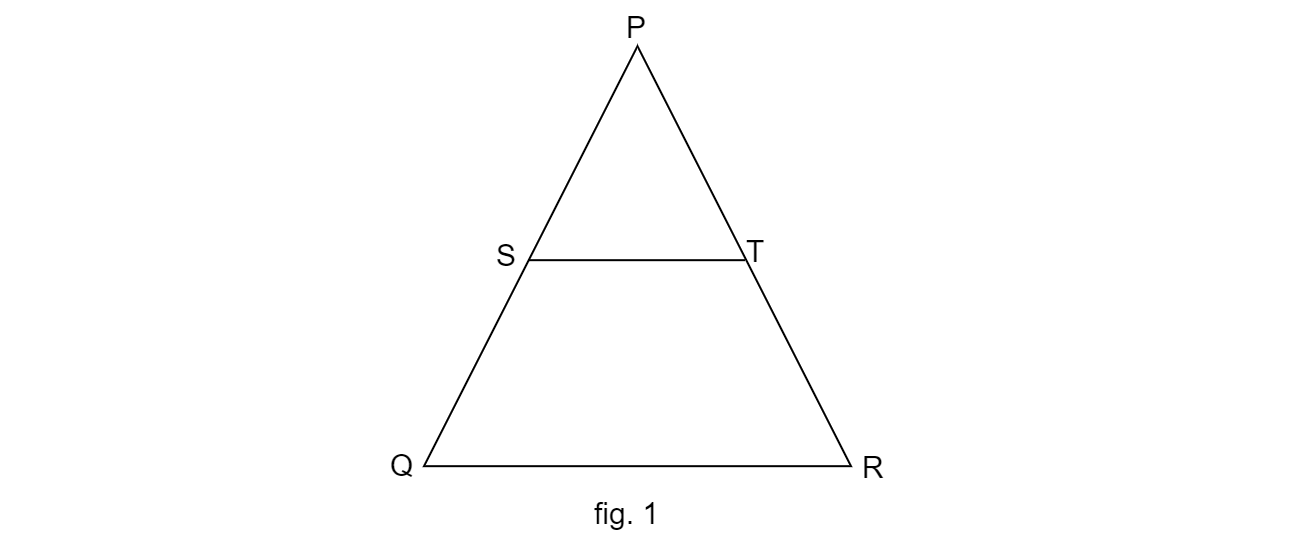
"\已知：在图 1 中 $\vartriangle$ PQR PT$=2$ 厘米，TR$=4$ 厘米，且 ST$\parallel$QR要求：求面积(ΔPST) 和面积(ΔPQR) 的比值 $\ ( \vartriangle PST) ∶area( \vartriangle PQR) =?$解：已知 $\displaystyle PT=2\ cm, \ TR=4\ cm\ $ 且 $ST\| QR$ $In\ \vartriangle PST\ and\ \vartriangle PQR$ $\angle PST=\angle PQR$ $\angle PTS=\angle PRQ$ $\angle P=\angle P$ $\Rightarrow \ ΔPST\sim ΔPQR\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ... 阅读更多
"\已知：三角形的底 $= 8$三角形的斜边 $= 17$要求：求给定三角形的周长和面积。解：根据勾股定理，$Base^2 + Height^2 = Hypotenuse^2$$8^2 + Height^2 = 17^2 $$64 + Height^2 = 289$$Height^2 = 289 - 64$$Height^2 = 225$$Height^2 = 15^2$$Height = 15$直角三角形的面积 $= \frac{1}{2} \times base \times height$ $= \frac{1}{2} \times 8 \times 15$ $ = 4 \times 15 = 60$因此，三角形的面积为 60 平方单位。三角形的周长 $=$ 三角形所有边的和。周长 $=8 + 15 + 17$ $ = 40$因此，三角形的周长为 40 个单位。
已知：连接两点 $A( 3, \ -5)$ 和 $B( -4, \ 8)$ 的线段，线段上的一点 P 使得 $\frac{AP}{PB} =\frac{K}{1}$，并且 P 也在直线 $x+y=0$ 上。要求：求 k 的值。解：已知如果有一条连接两点 $(x_{1} ,\ y_{1})$ 和 $( x_{2} ,\ y_{2} )$ 的线段，并且如果有一点 $P( x, \ y)$ 将线段按 m:n 的比例分成两部分，那么 $P( x, \ y) =\left(\frac{nx_{1} +mx_{2}}{m+n} ,\ \frac{ny_{1} +my_{2}}{m+n}\right)$ 这里 $m=k, \ n=1, \ x_{1} =3, \ y_{1} =-5, \ x_{2} =-4\ and\ y_{2} =8$使用分段 ... 阅读更多
已知：$tan\theta +cot\theta =5$。要求：求 $tan^{2} \theta +cot^{2} \theta $ 的值。解：已知，$tan\theta +cot\theta =5$两边平方，$( tan\theta +cot\theta )^{2} =5^{2}$$\Rightarrow tan^{2} \theta +cot^{2} \theta +2tan\theta cot\theta =25$$\Rightarrow tan^{2} \theta +cot^{2} \theta +2=25$$\Rightarrow tan^{2} \theta +cot^{2} \theta =25-2$$\Rightarrow tan^{2} \theta +cot^{2} \theta =23$
已知：两个零点 $3+\sqrt{2}$ 和 $ 3-\sqrt{2}$。要求：构造一个具有给定零点的二次多项式。解：这里，零点的和 $S=( \alpha +\beta ) $ $=\left( 3+\sqrt{2}\right) +\left( 3-\sqrt{2}\right) =6$给定零点的积，$P=( \alpha \times \beta )$ $=\left( 3+\sqrt{2}\right) \times \left( 3-\sqrt{2}\right) $$=3^{2} -\left(\sqrt{2}\right)^{2} =9-2=7$ 已知，如果 $\alpha $ 和 $\beta$ 是一个二次多项式的两个零点，那么该多项式为，$x^{2} -Sx+P$代入 $S$ 和 $P$ 的值，得到 $x^{2} -6x+7$