
离散数学速查指南
离散数学 - 导论
数学可以大致分为两类:
连续数学 - 它基于连续数轴或实数。其特点是任意两数之间几乎总存在无限多个数。例如,连续数学中的函数可以用一条没有间断的光滑曲线绘制。
离散数学 - 它涉及离散值;即任意两点之间只有可数个点。例如,如果我们有一组有限的对象,则该函数可以定义为这些对象的序偶列表,并且可以表示为这些序偶的完整列表。
离散数学中的主题
虽然离散数学的分支数量无法确定,但在任何关于此问题的研究中,几乎总是会涵盖以下主题:
- 集合、关系和函数
- 数理逻辑
- 群论
- 计数理论
- 概率
- 数学归纳法和递推关系
- 图论
- 树
- 布尔代数
我们将在本教程的后续章节中讨论这些概念。
离散数学 - 集合
德国数学家G. 康托尔引入了集合的概念。他将集合定义为通过某种规则或描述选择的确定且可区分对象的集合。
集合理论构成了计数理论、关系、图论和有限状态机等其他几个研究领域的基础。在本章中,我们将介绍集合论的不同方面。
集合 - 定义
集合是不同元素的无序集合。集合可以用集合括号列出其元素来明确地写出。如果元素的顺序改变或集合的任何元素重复,则不会对集合产生任何改变。
集合的一些例子
- 所有正整数的集合
- 太阳系中所有行星的集合
- 印度所有邦的集合
- 所有小写字母的集合
集合的表示
集合可以用两种方式表示:
- 列举法或表格法
- 集合构造器表示法
列举法或表格法
集合通过列出构成它的所有元素来表示。元素用大括号括起来,并用逗号分隔。
例1 - 英文字母表中元音的集合,$A = \lbrace a,e,i,o,u \rbrace$
例2 - 小于10的奇数集合,$B = \lbrace 1,3,5,7,9 \rbrace$
集合构造器表示法
集合通过指定集合元素共有的属性来定义。集合描述为 $A = \lbrace x : p(x) \rbrace$
例1 - 集合 $\lbrace a,e,i,o,u \rbrace$ 写作:
$A = \lbrace x : \text{x是英文字母表中的元音} \rbrace$
例2 - 集合 $\lbrace 1,3,5,7,9 \rbrace$ 写作:
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
如果元素x是集合S的成员,则表示为$x \in S$;如果元素y不是集合S的成员,则表示为$y \notin S$。
例 - 如果 $S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ 但 $1.5 \notin S$
一些重要的集合
N - 所有自然数的集合 = $\lbrace1, 2, 3, 4, .....\rbrace$
Z - 所有整数的集合 = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z+ - 所有正整数的集合
Q - 所有有理数的集合
R - 所有实数的集合
W - 所有全数的集合
集合的基数
集合S的基数,用$|S|$表示,是集合的元素个数。这个数也称为基数。如果一个集合有无限多个元素,则其基数为$\infty$。
例 - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$
如果有两个集合X和Y,
$|X| = |Y|$ 表示两个集合X和Y具有相同的基数。当X中的元素个数正好等于Y中的元素个数时,就会发生这种情况。在这种情况下,存在从X到Y的双射函数'f'。
$|X| \le |Y|$ 表示集合X的基数小于或等于集合Y的基数。当X中的元素个数小于或等于Y中的元素个数时,就会发生这种情况。在这里,存在从X到Y的单射函数'f'。
$|X| \lt |Y|$ 表示集合X的基数小于集合Y的基数。当X中的元素个数小于Y中的元素个数时,就会发生这种情况。在这里,从X到Y的函数'f'是单射函数,但不是双射函数。
$如果\ |X| \le |Y| 和 |X| \ge |Y| 则 |X| = |Y|。集合X和Y通常被称为等价集合。
集合的类型
集合可以分为多种类型。其中一些是有限集、无限集、子集、全集、真子集、单元素集等。
有限集
包含确定数量元素的集合称为有限集。
例 - $S = \lbrace x \:| \:x \in N$ and $70 \gt x \gt 50 \rbrace$
无限集
包含无限多个元素的集合称为无限集。
例 - $S = \lbrace x \: | \: x \in N $ and $ x \gt 10 \rbrace$
子集
如果集合X的每个元素都是集合Y的元素,则集合X是集合Y的子集(写成$X \subseteq Y$)。
例1 - 令,$X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。这里集合Y是集合X的子集,因为集合Y的所有元素都在集合X中。因此,我们可以写成$Y \subseteq X$。
例2 - 令,$X = \lbrace 1, 2, 3 \rbrace$ 和 $Y = \lbrace 1, 2, 3 \rbrace$。这里集合Y是集合X的子集(不是真子集),因为集合Y的所有元素都在集合X中。因此,我们可以写成$Y \subseteq X$。
真子集
“真子集”可以定义为“子集但不等”。如果集合X的每个元素都是集合Y的元素并且$|X| \lt |Y|$,则集合X是集合Y的真子集(写成$ X \subset Y $)。
例 - 令,$X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。这里集合$Y \subset X$,因为Y中的所有元素也包含在X中,并且X至少比集合Y多一个元素。
全集
它是特定上下文或应用程序中所有元素的集合。该上下文或应用程序中的所有集合本质上都是这个全集的子集。全集表示为$U$。
例 - 我们可以将$U$定义为地球上所有动物的集合。在这种情况下,所有哺乳动物的集合是$U$的子集,所有鱼类的集合是$U$的子集,所有昆虫的集合是$U$的子集,等等。
空集或零集
空集不包含任何元素。它用$\emptyset$表示。由于空集中的元素数量是有限的,因此空集是有限集。空集或零集的基数为零。
例 - $S = \lbrace x \:| \: x \in N$ and $7 \lt x \lt 8 \rbrace = \emptyset$
单元素集或单元集
单元素集或单元集只包含一个元素。单元素集用$\lbrace s \rbrace$表示。
例 - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
相等集
如果两个集合包含相同的元素,则称它们相等。
例 - 如果$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 1, 2 \rbrace$,则它们相等,因为集合A的每个元素都是集合B的元素,集合B的每个元素都是集合A的元素。
等价集
如果两个集合的基数相同,则称它们为等价集。
例 - 如果$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 16, 17, 22 \rbrace$,则它们是等价的,因为A的基数等于B的基数。即$|A| = |B| = 3$
重叠集
至少有一个公共元素的两个集合称为重叠集。
对于重叠集:
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
例 - 令,$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 12, 42 \rbrace$。有一个公共元素'6',因此这些集合是重叠集。
不相交集
如果两个集合A和B没有任何公共元素,则称它们为不相交集。因此,不相交集具有以下性质:
$n(A \cap B) = \emptyset$
$n(A \cup B) = n(A) + n(B)$
例 - 令,$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 7, 9, 14 \rbrace$,没有一个公共元素,因此这些集合是不相交集。
维恩图
维恩图是由John Venn于1880年发明的,它是一个示意图,显示了不同数学集合之间所有可能的逻辑关系。
例子
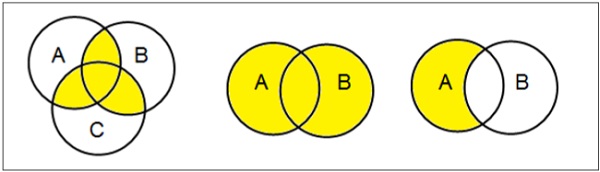
集合运算
集合运算包括集合并、集合交、集合差、集合补和笛卡尔积。
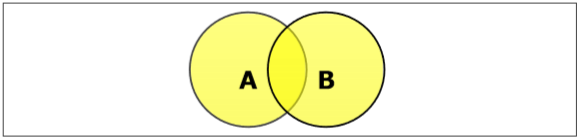
集合并
集合A和B的并集(用$A \cup B$表示)是属于A、属于B或同时属于A和B的元素的集合。因此,$A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$。
例 - 如果$A = \lbrace 10, 11, 12, 13 \rbrace$ 和 B = $\lbrace 13, 14, 15 \rbrace$,则$A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$。(公共元素只出现一次)
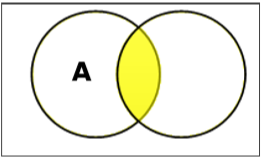
集合交集
集合 A 和 B 的交集(记作 $A \cap B$)是既属于 A 又属于 B 的元素的集合。因此,$A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$。
示例 − 如果 $A = \lbrace 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,则 $A \cap B = \lbrace 13 \rbrace$。
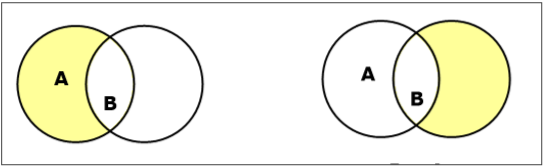
集合差/相对补集
集合 A 和 B 的集合差(记作 $A – B$)是只属于 A 但不属于 B 的元素的集合。因此,$A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$。
示例 − 如果 $A = \lbrace 10, 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,则 $(A - B) = \lbrace 10, 11, 12 \rbrace$ 且 $(B - A) = \lbrace 14, 15 \rbrace$。这里我们可以看到 $(A - B) \ne (B - A)$
集合的补集
集合 A 的补集(记作 $A’$)是不属于集合 A 的元素的集合。因此,$A' = \lbrace x | x \notin A \rbrace$。
更具体地说,$A'= (U - A)$,其中 $U$ 是包含所有对象的全集。
示例 − 如果 $A = \lbrace x \:| \: x\ \: {属于奇数整数集合} \rbrace$,则 $A' = \lbrace y\: | \: y\ \: {不属于奇数整数集合} \rbrace$
笛卡尔积/叉积
n 个集合 $A_1, A_2, \dots A_n$ 的笛卡尔积记作 $A_1 \times A_2 \dots \times A_n$,可以定义为所有可能的序对 $(x_1, x_2, \dots x_n)$,其中 $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$
示例 − 如果我们取两个集合 $A = \lbrace a, b \rbrace$ 和 $B = \lbrace 1, 2 \rbrace$,
A 和 B 的笛卡尔积写成 − $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
B 和 A 的笛卡尔积写成 − $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
幂集
集合 S 的幂集是 S 的所有子集的集合,包括空集。基数为 n 的集合 S 的幂集的基数为 $2^n$。幂集记作 $P(S)$。
示例 −
对于集合 $S = \lbrace a, b, c, d \rbrace$,让我们计算子集 −
包含 0 个元素的子集 − $\lbrace \emptyset \rbrace$(空集)
包含 1 个元素的子集 − $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$
包含 2 个元素的子集 − $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$
包含 3 个元素的子集 − $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
包含 4 个元素的子集 − $\lbrace a, b, c, d \rbrace$
因此,$P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S) | = 2^4 = 16$
注意 − 空集的幂集也是空集。
$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
集合的划分
集合 S 的划分是 n 个不相交子集(例如 $P_1, P_2, \dots P_n$)的集合,满足以下三个条件:
$P_i$ 不包含空集。
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ 对所有\ 0 \lt i \le n \rbrack$
子集的并集必须等于整个原始集合。
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
任意两个不同的集合的交集为空集。
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ 对 a \ne b\ 其中 n \ge a,\: b \ge 0 \rbrack$
示例
设 $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
一个可能的划分是 $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
另一个可能的划分是 $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
贝尔数
贝尔数给出划分集合的方法数量。它们记作 $B_n$,其中 n 是集合的基数。
示例 −
设 $S = \lbrace 1, 2, 3\rbrace$,$n = |S| = 3$
另一种划分是 −
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
因此 $B_3 = 5$
离散数学 - 关系
每当讨论集合时,集合元素之间的关系就是接下来要讨论的事情。集合内对象之间或两个或多个集合的对象之间可能存在关系。
定义和性质
从集合 x 到 y 的二元关系 R(写成 $xRy$ 或 $R(x,y)$)是笛卡尔积 $x \times y$ 的一个子集。如果 G 的有序对反转,关系也会改变。
一般来说,集合 $A_1, \dots ,\ 和\ A_n$ 之间的 n 元关系 R 是 n 元积 $A_1 \times \dots \times A_n$ 的一个子集。在这种情况下,关系 R 的最小基数为零,最大基数为 $n^2$。
单个集合 A 上的二元关系 R 是 $A \times A$ 的一个子集。
对于两个不同的集合 A 和 B,其基数分别为 *m* 和 *n*,从 A 到 B 的关系 R 的最大基数为 *mn*。
定义域和值域
如果有两个集合 A 和 B,并且关系 R 有序对 (x, y),则:
R 的定义域 Dom(R) 是集合 $\lbrace x \:| \: (x, y) \in R \:对于某个 y\ 在\ B 中 \rbrace$
R 的值域 Ran(R) 是集合 $\lbrace y\: |\: (x, y) \in R \:对于某个 x\ 在\ A 中 \rbrace$
例子
设,$A = \lbrace 1, 2, 9 \rbrace $ 且 $ B = \lbrace 1, 3, 7 \rbrace$
情况 1 − 如果关系 R 是“等于”,则 $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom(R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
情况 2 − 如果关系 R 是“小于”,则 $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom(R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
情况 3 − 如果关系 R 是“大于”,则 $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom(R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
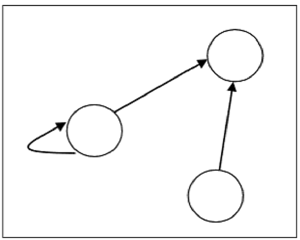
使用图形表示关系
关系可以使用有向图来表示。
图中顶点的数量等于定义关系的集合中元素的数量。对于关系 R 中的每个有序对 (x, y),都会有一条从顶点“x”到顶点“y”的有向边。如果存在有序对 (x, x),则顶点“x”上将会有自环。
假设,集合 $S = \lbrace 1, 2, 3 \rbrace$ 上存在关系 $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$,它可以用下图表示:
关系的类型
集合 X 和 Y 之间或 E 上的空关系是空集 $\emptyset$
集合 X 和 Y 之间的全关系是集合 $X \times Y$
集合 X 上的恒等关系是集合 $\lbrace (x, x) | x \in X \rbrace$
关系 R 的逆关系 R' 定义为 − $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
示例 − 如果 $R = \lbrace (1, 2), (2, 3) \rbrace$,则 $R'$ 将为 $\lbrace (2, 1), (3, 2) \rbrace$
如果 $\forall a \in A$ 与 a 相关(成立 aRa),则集合 A 上的关系 R 称为自反的
示例 − 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, a), (b, b) \rbrace$ 是自反的。
如果不存在 $a \in A$ 与 a 相关(不成立 aRa),则集合 A 上的关系 R 称为反自反的。
示例 − 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, b), (b, a) \rbrace$ 是反自反的。
如果 $xRy$ 蕴含 $yRx$,$\forall x \in A$ 且 $\forall y \in A$,则集合 A 上的关系 R 称为对称的。
示例 − 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ 是对称的。
如果 $xRy$ 且 $yRx$ 蕴含 $x = y \: \forall x \in A$ 且 $\forall y \in A$,则集合 A 上的关系 R 称为反对称的。
示例 − 关系 $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ 是反对称的,因为 $x \leq y$ 且 $y \leq x$ 蕴含 $x = y$。
如果 $xRy$ 且 $yRz$ 蕴含 $xRz, \forall x,y,z \in A$,则集合 A 上的关系 R 称为传递的。
示例 − 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ 是传递的。
如果关系是自反的、对称的和传递的,则它是等价关系。
示例 − 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ 是等价关系,因为它既是自反的、对称的,又是传递的。
离散数学 - 函数
函数将集合的每个元素精确地分配给相关集合的一个元素。函数在各个领域都有其应用,例如表示算法的计算复杂度、计数对象、研究序列和字符串等。本部分的第三章也是最后一章重点介绍了函数的重要方面。
函数 - 定义
函数或映射(定义为 $f: X \rightarrow Y$)是从一个集合 X 的元素到另一个集合 Y 的元素的关系(X 和 Y 是非空集合)。X 称为函数 'f' 的定义域,Y 称为函数 'f' 的陪域。
函数 'f' 是 X 和 Y 上的关系,使得对于每个 $x \in X$,都存在唯一的 $y \in Y$,使得 $(x,y) \in R$。“x”称为原像,“y”称为函数 f 的像。
函数可以是一对一的或多对一的,但不能是一对多的。
单射/一对一函数
如果对于每个 $b \in B$,最多存在一个 $a \in A$ 使得 $f(s) = t$,则函数 $f: A \rightarrow B$ 是单射或一对一函数。
这意味着如果 $a_1 \ne a_2$ 蕴含 $f(a1) \ne f(a2)$,则函数f是单射的。
示例
$f: N \rightarrow N, f(x) = 5x$ 是单射的。
$f: N \rightarrow N, f(x) = x^2$ 是单射的。
$f: R\rightarrow R, f(x) = x^2$ 不是单射的,因为 $(-x)^2 = x^2$
满射/到函数
函数 $f: A \rightarrow B$ 是满射(映上)的,如果 f 的像等于其值域。等价地,对于每一个 $b \in B$,都存在某个 $a \in A$ 使得 $f(a) = b$。这意味着对于 B 中的任何 y,都存在 A 中的某个 x 使得 $y = f(x)$。
示例
$f : N \rightarrow N, f(x) = x + 2$ 是满射的。
$f : R \rightarrow R, f(x) = x^2$ 不是满射的,因为我们找不到一个平方为负数的实数。
双射/一一对应
函数 $f: A \rightarrow B$ 是双射或一一对应的,当且仅当 **f** 既是单射又是满射。
问题
证明由 $f(x) = 2x – 3$ 定义的函数 $f: R \rightarrow R$ 是双射函数。
**解释** − 我们必须证明此函数既是单射又是满射。
如果 $f(x_1) = f(x_2)$,则 $2x_1 – 3 = 2x_2 – 3$,这意味着 $x_1 = x_2$。
因此,f 是 **单射** 的。
这里,$2x – 3= y$
所以,$x = (y+3)/2$,属于 R,并且 $f(x) = y$。
因此,f 是 **满射** 的。
由于 **f** 既是 **满射** 又 是 **单射** 的,所以我们可以说 **f** 是 **双射** 的。
函数的反函数
一一对应函数 $f : A \rightarrow B$ 的 **反函数** 是函数 $g : B \rightarrow A$,它满足以下性质 −
$f(x) = y \Leftrightarrow g(y) = x$
如果存在反函数 g,则称函数 f 可逆。
示例
函数 $f : Z \rightarrow Z, f(x)=x+5$ 是可逆的,因为它具有反函数 $ g : Z \rightarrow Z, g(x)= x-5$。
函数 $f : Z \rightarrow Z, f(x)=x^2$ 不可逆,因为它不是一一对应的,因为 $(-x)^2=x^2$。
函数的复合
两个函数 $f: A \rightarrow B$ 和 $g: B \rightarrow C$ 可以复合得到一个复合函数 $g o f$。这是一个从 A 到 C 的函数,定义为 $(gof)(x) = g(f(x))$
示例
设 $f(x) = x + 2$ 和 $g(x) = 2x + 1$,求 $( f o g)(x)$ 和 $( g o f)(x)$。
解答
$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
因此,$(f o g)(x) \neq (g o f)(x)$
关于复合的一些事实
如果 f 和 g 是一一对应的,则函数 $(g o f)$ 也是一一对应的。
如果 f 和 g 是满射的,则函数 $(g o f)$ 也是满射的。
复合总是满足结合律,但不满足交换律。
离散数学 - 命题逻辑
数学逻辑的规则指定了推理数学命题的方法。希腊哲学家亚里士多德是逻辑推理的先驱。逻辑推理为许多数学领域以及计算机科学提供了理论基础。它在计算机科学中有很多实际应用,例如计算机器的设计、人工智能、编程语言的数据结构的定义等。
**命题逻辑**关注的是可以赋予其真值“真”和“假”的语句。其目的是分析这些语句,无论是单独的还是组合的。
命题逻辑 – 定义
命题是由声明性语句组成的集合,具有真值“真”或真值“假”。命题由命题变量和连接词组成。我们用大写字母(A、B 等)表示命题变量。连接词连接命题变量。
下面给出一些命题的例子 −
- “人是凡人”,返回真值“真”
- “12 + 9 = 3 – 2”,返回真值“假”
以下不是命题 −
“A 小于 2”。这是因为除非我们给 A 一个特定的值,否则我们无法说这个语句是真还是假。
连接词
在命题逻辑中,我们通常使用五种连接词,它们是 −
或 ($\lor$)
与 ($\land$)
否定/非 ($\lnot$)
蕴含/如果-那么 ($\rightarrow$)
当且仅当 ($\Leftrightarrow$)。
**或 ($\lor$)** − 两个命题 A 和 B 的或运算(写成 $A \lor B$)如果命题变量 A 或 B 中至少有一个为真,则为真。
真值表如下 −
| A | B | A ∨ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 真 |
| 假 | 真 | 真 |
| 假 | 假 | 假 |
**与 ($\land$)** − 两个命题 A 和 B 的与运算(写成 $A \land B$)如果命题变量 A 和 B 都为真,则为真。
真值表如下 −
| A | B | A ∧ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 假 |
| 假 | 假 | 假 |
**否定 ($\lnot$)** − 命题 A 的否定(写成 $\lnot A$)在 A 为真时为假,在 A 为假时为真。
真值表如下 −
| A | ¬ A |
|---|---|
| 真 | 假 |
| 假 | 真 |
**蕴含/如果-那么 ($\rightarrow$)** − 蕴含 $A \rightarrow B$ 是命题“如果 A,那么 B”。如果 A 为真而 B 为假,则为假。其余情况为真。
真值表如下 −
| A | B | A → B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 真 |
| 假 | 假 | 真 |
**当且仅当 ($ \Leftrightarrow $)** − $A \Leftrightarrow B$ 是双条件逻辑连接词,当 p 和 q 相同时为真,即两者都为假或两者都为真。
真值表如下 −
| A | B | A ⇔ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 假 |
| 假 | 假 | 真 |
重言式
重言式是一个公式,对于其命题变量的每个值始终为真。
**示例** − 证明 $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ 是重言式
真值表如下 −
| A | B | A → B | (A → B) ∧ A | [( A → B ) ∧ A] → B |
|---|---|---|---|---|
| 真 | 真 | 真 | 真 | 真 |
| 真 | 假 | 假 | 假 | 真 |
| 假 | 真 | 真 | 假 | 真 |
| 假 | 假 | 真 | 假 | 真 |
正如我们所看到的,$\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ 的每个值都是“真”,它是一个重言式。
矛盾式
矛盾式是一个公式,对于其命题变量的每个值始终为假。
**示例** − 证明 $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 是矛盾式
真值表如下 −
| A | B | A ∨ B | ¬ A | ¬ B | (¬ A) ∧ ( ¬ B) | (A ∨ B) ∧ [( ¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| 真 | 真 | 真 | 假 | 假 | 假 | 假 |
| 真 | 假 | 真 | 假 | 真 | 假 | 假 |
| 假 | 真 | 真 | 真 | 假 | 假 | 假 |
| 假 | 假 | 假 | 真 | 真 | 真 | 假 |
正如我们所看到的,$(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 的每个值都是“假”,它是一个矛盾式。
偶然式
偶然式是一个公式,对于其命题变量的每个值,它既有一些真值,也有一些假值。
**示例** − 证明 $(A \lor B) \land (\lnot A)$ 是偶然式
真值表如下 −
| A | B | A ∨ B | ¬ A | (A ∨ B) ∧ (¬ A) |
|---|---|---|---|---|
| 真 | 真 | 真 | 假 | 假 |
| 真 | 假 | 真 | 假 | 假 |
| 假 | 真 | 真 | 真 | 真 |
| 假 | 假 | 假 | 真 | 假 |
正如我们所看到的,$(A \lor B) \land (\lnot A)$ 的每个值都既有“真”也有“假”,它是一个偶然式。
命题等价
如果满足以下两个条件中的任何一个,则两个语句 X 和 Y 在逻辑上是等价的 −
每个语句的真值表具有相同的真值。
双条件语句 $X \Leftrightarrow Y$ 是重言式。
**示例** − 证明 $\lnot (A \lor B)$ 和 $\lbrack (\lnot A) \land (\lnot B) \rbrack$ 是等价的
使用第一种方法(匹配真值表)进行测试
| A | B | A ∨ B | ¬ (A ∨ B) | ¬ A | ¬ B | [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| 真 | 真 | 真 | 假 | 假 | 假 | 假 |
| 真 | 假 | 真 | 假 | 假 | 真 | 假 |
| 假 | 真 | 真 | 假 | 真 | 假 | 假 |
| 假 | 假 | 假 | 真 | 真 | 真 | 真 |
在这里,我们可以看到 $\lnot (A \lor B)$ 和 $\lbrack (\lnot A) \land (\lnot B) \rbrack$ 的真值相同,因此这两个语句是等价的。
使用第二种方法(双条件)进行测试
| A | B | ¬ (A ∨ B ) | [(¬ A) ∧ (¬ B)] | [¬ (A ∨ B)] ⇔ [(¬ A ) ∧ (¬ B)] |
|---|---|---|---|---|
| 真 | 真 | 假 | 假 | 真 |
| 真 | 假 | 假 | 假 | 真 |
| 假 | 真 | 假 | 假 | 真 |
| 假 | 假 | 真 | 真 | 真 |
由于 $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ 是重言式,因此这两个语句是等价的。
逆命题、否命题和逆否命题
蕴含/如果-那么 $(\rightarrow)$ 也称为条件语句。它有两个部分 −
- 假设,p
- 结论,q
如前所述,它表示为 $p \rightarrow q$。
**条件语句示例** − “如果你做作业,你就不会受到惩罚。”在这里,“你做作业”是假设 p,“你不会受到惩罚”是结论 q。
**逆命题** − 条件语句的逆命题是对假设和结论的否定。如果语句是“如果 p,那么 q”,则逆命题将是“如果非 p,那么非 q”。因此,$p \rightarrow q$ 的逆命题是 $ \lnot p \rightarrow \lnot q$。
**示例** − “如果你做作业,你就不会受到惩罚”的逆命题是“如果你不做作业,你就会受到惩罚”。
**否命题** − 条件语句的否命题是通过交换假设和结论来计算的。如果语句是“如果 p,那么 q”,则否命题将是“如果 q,那么 p”。$p \rightarrow q$ 的否命题是 $q \rightarrow p$。
**示例** − “如果你做作业,你就不会受到惩罚”的否命题是“如果你不会受到惩罚,你就会做作业”。
**逆否命题** − 条件语句的逆否命题是通过交换逆命题的假设和结论来计算的。如果语句是“如果 p,那么 q”,则逆否命题将是“如果非 q,那么非 p”。$p \rightarrow q$ 的逆否命题是 $\lnot q \rightarrow \lnot p$。
**示例** − “如果你做作业,你就不会受到惩罚”的逆否命题是“如果你受到了惩罚,你就没有做作业”。
对偶原理
对偶原理指出,对于任何真命题,通过将并集换成交集(反之亦然)并将全集换成空集(反之亦然)而获得的对偶命题也是真的。如果任何语句的对偶是语句本身,则称其为**自对偶**语句。
**示例** − $(A \cap B ) \cup C$ 的对偶是 $(A \cup B) \cap C$
范式
我们可以将任何命题转换为两种范式 −
- 合取范式
- 析取范式
合取范式
如果一个复合语句是通过对用或连接的变量(包括变量的否定)进行与运算而获得的,则它处于合取范式。就集合运算而言,它是通过对用并集连接的变量进行交集运算而获得的复合语句。
例子
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
析取范式
如果一个复合语句是通过对用与连接的变量(包括变量的否定)进行或运算而获得的,则它处于析取范式。就集合运算而言,它是通过对用交集连接的变量进行并集运算而获得的复合语句。
例子
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
离散数学 - 谓词逻辑
**谓词逻辑**处理谓词,谓词是包含变量的命题。
谓词逻辑 – 定义
谓词是在某个特定域上定义的一个或多个变量的表达式。通过为变量赋值或对变量进行量化,可以将包含变量的谓词转换为命题。
以下是一些谓词的例子 −
- 设 E(x, y) 表示“x = y”
- 设 X(a, b, c) 表示“a + b + c = 0”
- 设 M(x, y) 表示“x 与 y 结婚”
良构公式
良构公式 (wff) 是满足以下任何条件的谓词 −
所有命题常量和命题变量都是 wff
如果 x 是变量,Y 是 wff,则 $\forall x Y$ 和 $\exists x Y$ 也是 wff
真值和假值是 wff
每个原子公式都是 wff
连接 wff 的所有连接词都是 wff
量词
谓词的变量由量词量化。谓词逻辑中有两种类型的量词 − 全称量词和存在量词。
全称量词
全称量词指出其范围内的语句对于特定变量的每个值都是正确的。它用符号 $\forall$ 表示。
$\forall x P(x)$ 读作对于 x 的每个值,P(x) 都为真。
**示例** − “人是凡人”可以转换为命题形式 $\forall x P(x)$,其中 P(x) 是表示 x 是凡人的谓词,论域是所有男人。
存在量词
存在量词表示其作用范围内的语句对于特定变量的某些值是正确的。它用符号$\exists$表示。
$\exists x P(x)$ 读作:对于某些 x 值,P(x) 为真。
示例 − “有些人是不诚实的”可以转化为命题形式$\exists x P(x)$,其中 P(x) 是表示 x 不诚实的谓词,论域为某些人。
嵌套量词
如果我们使用的量词出现在另一个量词的作用范围内,则称为嵌套量词。
示例
$\forall\ a\: \exists b\: P (x, y)$,其中$P (a, b)$表示$a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$,其中$P (a, b, c)$表示$a + (b + c) = (a + b) + c$
注意 − $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
离散数学 - 推理规则
为了从我们已知其真值的语句中推导出新的语句,使用推理规则。
推理规则是做什么用的?
数学逻辑经常用于逻辑证明。证明是有效的论证,用于确定数学语句的真值。
论证是一系列语句。最后一个语句是结论,所有在其之前的语句都称为前提(或假设)。符号“$\therefore$”(读作因此)放在结论之前。有效论证是指结论遵循前提真值的论证。
推理规则为根据我们已有的语句构建有效论证提供模板或指导。
推理规则表
| 推理规则 | 名称 | 推理规则 | 名称 |
|---|---|---|---|
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ |
附加 |
$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$ |
析取三段论 |
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ |
合取 |
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$ |
假言三段论 |
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$ |
简化 |
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$ |
构造性困境 |
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$ |
肯定前件 |
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$ |
破坏性困境 |
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$ |
否定后件 |
附加
如果 P 是前提,我们可以使用附加规则推导出$P \lor Q$。
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$
示例
设 P 为命题,“他学习非常努力”为真。
因此 − “要么他学习非常努力,要么他是一个非常差的学生”。这里 Q 是命题“他是一个非常差的学生”。
合取
如果 P 和 Q 是两个前提,我们可以使用合取规则推导出$P \land Q$。
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$
示例
设 P − “他学习非常努力”
设 Q − “他是班上最好的男孩”
因此 − “他学习非常努力,而且他是班上最好的男孩”。
简化
如果$P \land Q$是一个前提,我们可以使用简化规则推导出 P。
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$
示例
“他学习非常努力,而且他是班上最好的男孩”,$P \land Q$
因此 − “他学习非常努力”。
肯定前件
如果 P 和$P \rightarrow Q$是两个前提,我们可以使用肯定前件推导出 Q。
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$
示例
“如果你有密码,那么你可以登录 Facebook”,$P \rightarrow Q$
“你有一个密码”,P
因此 − “你可以登录 Facebook”。
否定后件
如果$P \rightarrow Q$和$\lnot Q$是两个前提,我们可以使用否定后件推导出$\lnot P$。
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$
示例
“如果你有密码,那么你可以登录 Facebook”,$P \rightarrow Q$
“你无法登录 Facebook”,$\lnot Q$
因此 − “你没有密码”。
析取三段论
如果$\lnot P$和$P \lor Q$是两个前提,我们可以使用析取三段论推导出 Q。
$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$
示例
“冰淇淋不是香草味的”,$\lnot P$
“冰淇淋要么是香草味的,要么是巧克力味的”,$P \lor Q$
因此 − “冰淇淋是巧克力味的”。
假言三段论
如果$P \rightarrow Q$和$Q \rightarrow R$是两个前提,我们可以使用假言三段论推导出$P \rightarrow R$。
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$
示例
“如果下雨,我就不去上学”,$P \rightarrow Q$
“如果我不去上学,我就不用做作业”,$Q \rightarrow R$
因此 − “如果下雨,我就不用做作业”。
构造性困境
如果$( P \rightarrow Q ) \land (R \rightarrow S)$和$P \lor R$是两个前提,我们可以使用构造性困境推导出$Q \lor S$。
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$
示例
“如果下雨,我就请假”,$( P \rightarrow Q )$
“如果外面很热,我就去冲个澡”,$(R \rightarrow S)$
“要么下雨,要么外面很热”,$P \lor R$
因此 − “我要么请假,要么去冲个澡”。
破坏性困境
如果$(P \rightarrow Q) \land (R \rightarrow S)$和$ \lnot Q \lor \lnot S $是两个前提,我们可以使用破坏性困境推导出$\lnot P \lor \lnot R$。
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$
示例
“如果下雨,我就请假”,$(P \rightarrow Q )$
“如果外面很热,我就去冲个澡”,$(R \rightarrow S)$
“我要么不请假,要么不去冲澡”,$\lnot Q \lor \lnot S$
因此 − “要么不下雨,要么外面不热”。
运算符与公理
群论是数学和抽象代数的一个分支,它定义了一种名为群的代数结构。一般来说,群包含一组元素和一个在该组上的任何两个元素上的运算,以形成该组中的第三个元素。
1854年,英国数学家亚瑟·凯莱首次给出了群的现代定义:
“一组符号,它们彼此不同,并且任何两个符号的乘积(无论顺序如何),或任何一个符号自身的乘积,都属于该集合,则称该集合为一个群。这些符号通常不可交换[交换律],但具有结合律。”
在本章中,我们将了解构成集合论、群论和布尔代数基础的运算符和公理。
数学系统中的任何一组元素都可以用一组运算符和一些公理来定义。
在元素集合上定义的二元运算符是一个规则,它为每一对元素分配该集合中的唯一元素。例如,给定集合$ A = \lbrace 1, 2, 3, 4, 5 \rbrace $,如果它指定了根据对$(a,b)$查找 c 的规则,使得$a,b,c \in A$,那么我们可以说$\otimes$是运算$c = a \otimes b$的二元运算符。
数学系统的公理构成了可以从中推导出规则的基本假设。公理是:
封闭性
如果对于集合中的每一对元素,运算符都能找到该集合中的唯一元素,则该集合对于二元运算符是封闭的。
示例
设$A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
这个集合在二元运算符乘法$(\ast)$下是封闭的,因为对于运算$c = a \ast b$,对于任何$a, b \in A$,乘积$c \in A$。
该集合在二元运算符除法$(\div)$下不是封闭的,因为对于运算$c = a \div b$,对于任何$a, b \in A$,乘积 c 可能不在集合 A 中。如果$a = 7, b = 2$,则$c = 3.5$。这里$a,b \in A$但$c \notin A$。
结合律
集合 A 上的二元运算符$\otimes$在满足以下性质时是结合的:
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$,其中$x, y, z \in A $
示例
设$A = \lbrace 1, 2, 3, 4 \rbrace$
加法运算符$( + )$是结合的,因为对于任何三个元素$x,y,z \in A$,性质$(x + y) + z = x + ( y + z )$都成立。
减法运算符$( - )$不是结合的,因为
$$( x - y ) - z \ne x - ( y - z )$$
交换律
集合 A 上的二元运算符$\otimes$在满足以下性质时是交换的:
$x \otimes y = y \otimes x$,其中$x, y \in A$
示例
设$A = \lbrace 1, 2, 3, 4 \rbrace$
加法运算符$( + )$是交换的,因为对于任何两个元素$x,y \in A$,性质$x + y = y + x$都成立。
减法运算符$( - )$不是结合的,因为
$$x - y \ne y - x$$
分配律
集合 A 上的两个二元运算符$\otimes$和$\circledast$在满足以下性质时,$\otimes$对$\circledast$具有分配律:
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$,其中$x, y, z \in A $
示例
设$A = \lbrace 1, 2, 3, 4 \rbrace$
乘法运算符$( * )$和加法运算符$( + )$对加法运算符 + 具有分配律,因为对于任何三个元素$x,y,z \in A$,性质$x * ( y + z ) = ( x * y ) + ( x * z )$都成立。
但是,这些运算符对乘法运算符$*$不具有分配律,因为
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
单位元
如果存在一个元素$e \in A$,使得满足以下性质,则集合 A 对于 A 上的二元运算$\otimes$具有单位元:
$e \otimes x = x \otimes e$,其中$x \in A$
示例
设$Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
元素 1 是关于运算符$*$的单位元,因为对于任何元素$x \in Z$,
$$1 * x = x * 1$$
另一方面,减法运算$( - )$没有单位元。
逆元
如果集合 A 关于二元运算符 $\otimes$ 有一个幺元 $e$,那么当且仅当对于集合 A 中的每一个元素 $x$,都存在另一个元素 $y \in A$,使得下列性质成立时,我们就说集合 A 有逆元。
$$x \otimes y = e$$
示例
令 $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
给定加法运算 $(+)$ 和 $e = 0$,任何元素 x 的逆元是 $(-x)$,因为 $x + (-x) = 0$
德摩根律
德摩根律给出了两个(或多个)集合的并集和交集与其补集之间的一对变换。这些定律是:
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
示例
令 $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$,以及
全集 $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
因此,我们可以看到 $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
因此,我们可以看到 $(A \cap B)' = A' \cup B'$
离散数学 - 群论
半群
具有二元运算 $‘\omicron’$(复合运算)的有限或无限集合 $‘S’$ 称为半群,如果它同时满足以下两个条件:
封闭性 - 对于每一个 $(a, b) \in S$,$(a \omicron b)$ 都必须存在于集合 S 中。
结合律 - 对于每一个元素 $a, b, c \in S$,$(a \omicron b) \omicron c = a \omicron (b \omicron c)$ 必须成立。
示例
具有加法运算的正整数集(不包括零)是一个半群。例如,$S = \lbrace 1, 2, 3, \dots \rbrace$
这里封闭性成立,因为对于每一对 $(a, b) \in S$,$(a + b)$ 都存在于集合 S 中。例如,$1 + 2 = 3 \in S$
结合律也适用于每一个元素 $a, b, c \in S$,$(a + b) + c = a + (b + c)$。例如,$(1 + 2) + 3 = 1 + (2 + 3) = 6$
幺半群
幺半群是一个具有幺元的半群。集合 S 的幺元(用 $e$ 或 E 表示)是一个元素,使得对于 S 中的每一个元素 $a$,$(a \omicron e) = a$ 都成立。幺元也称为单位元。因此,幺半群同时满足三个性质:封闭性、结合律、幺元。
示例
具有乘法运算的正整数集(不包括零)是一个幺半群。$S = \lbrace 1, 2, 3, \dots \rbrace$
这里封闭性成立,因为对于每一对 $(a, b) \in S$,$(a \times b)$ 都存在于集合 S 中。[例如,$1 \times 2 = 2 \in S$,等等]
结合律也适用于每一个元素 $a, b, c \in S$,$(a \times b) \times c = a \times (b \times c)$ [例如,$(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$,等等]
幺元性质也适用于 S 中的每一个元素 $a$,$(a \times e) = a$ [例如,$(2 \times 1) = 2, (3 \times 1) = 3$,等等]。这里的幺元是 1。
群
群是一个具有逆元的幺半群。集合 S 的逆元(用 I 表示)是一个元素,使得对于 S 中的每一个元素 $a$,$(a \omicron I) = (I \omicron a) = a$ 都成立。因此,群同时满足四个性质:i) 封闭性,ii) 结合律,iii) 幺元,iv) 逆元。群 G 的阶是 G 中元素的数量,群中一个元素的阶是最小的正整数 n,使得 $a^n$ 是该群 G 的幺元。
例子
在矩阵乘法运算下,$N \times N$ 非奇异矩阵的集合构成一个群。
两个 $N \times N$ 非奇异矩阵的乘积也是一个 $N \times N$ 非奇异矩阵,这满足封闭性。
矩阵乘法本身是结合的。因此,结合律成立。
$N \times N$ 非奇异矩阵的集合包含单位矩阵,满足幺元性质。
由于所有矩阵都是非奇异的,它们都有逆元,这些逆元也是非奇异矩阵。因此,逆元性质也成立。
阿贝尔群
阿贝尔群 G 是一个群,对于 G 中的每一对元素 $(a, b)$,交换律都成立。因此,群同时满足五个性质:i) 封闭性,ii) 结合律,iii) 幺元,iv) 逆元,v) 交换律。
示例
具有加法运算的正整数集(包括零)是一个阿贝尔群。$G = \lbrace 0, 1, 2, 3, \dots \rbrace$
这里封闭性成立,因为对于每一对 $(a, b) \in S$,$(a + b)$ 都存在于集合 S 中。[例如,$1 + 2 = 3 \in S$,等等]
结合律也适用于每一个元素 $a, b, c \in S$,$(a + b) + c = a + (b + c)$ [例如,$(1 + 2) + 3 = 1 + (2 + 3) = 6$,等等]
幺元性质也适用于 S 中的每一个元素 $a$,$(a + e) = a$ [例如,$(2 + 0) = 2, (3 + 0) = 3$,等等]。这里的幺元是 0。
交换律也适用于 S 中的每一个元素 $a, b$,$(a + b) = (b + a)$ [例如,$(2 + 3) = (3 + 2) = 5$,等等]
循环群和子群
循环群是可以由单个元素生成的群。循环群的每一个元素都是某个特定元素的幂,这个特定元素称为生成元。循环群可以由生成元'g'生成,使得群的每一个其他元素都可以写成生成元'g'的幂。
示例
在乘法运算下,复数集 $\lbrace 1, -1, i, -i \rbrace$ 是一个循环群。
有两个生成元:$i$ 和 $-i$,因为 $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$,以及 $(-i)^1 = -i, (-i)^2 = -1, (-i)^3 = i, (-i)^4 = 1$,涵盖了群的所有元素。因此,它是一个循环群。
注意 - 循环群总是阿贝尔群,但并非所有阿贝尔群都是循环群。在加法运算下的有理数不是循环群,但它是阿贝尔群。
如果子群 H 是群 G 的一个子集(记作 $H ≤ G$),则它同时满足四个性质:封闭性、结合律、幺元和逆元。
群 G 的子群 H 如果不包含整个群 G,则称为真子群(记作 $H < G$)。循环群的子群是循环群,阿贝尔群的子群也是阿贝尔群。
示例
令群 $G = \lbrace 1, i, -1, -i \rbrace$
则一些子群是 $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1, -1 \rbrace$,
这不是子群:$H_3 = \lbrace 1, i \rbrace$,因为 $(i)^{-1} = -i$ 不在 $H_3$ 中
偏序集 (POSET)
偏序集由一个集合和一个二元关系组成,该二元关系是自反的、反对称的和传递的。“偏序集”缩写为 POSET。
例子
在小于等于 $(\le)$ 二元运算下的实数集是一个偏序集。
令集合 $S = \lbrace 1, 2, 3 \rbrace$,运算符是 $\le$
关系将是 $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
由于 $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$,此关系 R 是自反的
此关系 R 是反对称的,因为
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R$ 且 $\lbrace (2, 1), (3, 1), (3, 2) \rbrace \notin R$
此关系 R 也是传递的,因为 $\lbrace (1, 2), (2, 3), (1, 3)\rbrace \in R$。
因此,它是一个偏序集。
在“可达性”运算下的有向无环图的顶点集是一个偏序集。
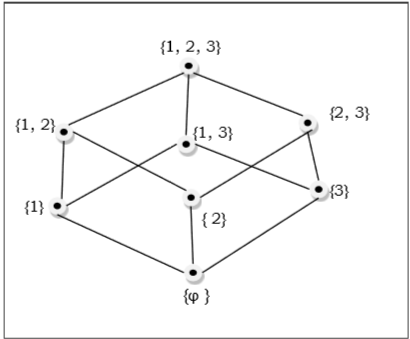
哈斯图
偏序集的哈斯图是有向图,其顶点是该偏序集的元素,弧覆盖偏序集中的对 (x, y)。如果在偏序集中 $x < y$,则点 x 出现在哈斯图中点 y 的下方。如果在偏序集中 $x < y < z$,则 x 和 z 之间的箭头不会显示,因为它是隐含的。
示例
$\lbrace 1, 2, 3 \rbrace$ 的子集的偏序集 $\lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ 由以下哈斯图所示:
全序集
全序集或线性序集是一个偏序集,其中每一对元素都是可比较的。如果 $a \le b$ 或 $b \le a$ 成立,则元素 $a, b \in S$ 被称为可比较的。三元性定律定义了这个全序集。全序集可以定义为一个分配格,它具有性质 $\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$,对于集合 S 中 a 和 b 的所有值都成立。
示例
由 $\subseteq$ 序的 $\lbrace a, b \rbrace$ 的幂集是一个全序集,因为幂集 $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b \rbrace \rbrace$ 的所有元素都是可比较的。
非全序集的例子
在运算 x 整除 y 下的集合 $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 不是全序集。
这里,对于所有 $(x, y) \in S$,$x | y$ 都必须成立,但这不意味着 2 | 3,因为 2 不整除 3,或者 3 不整除 2。因此,它不是全序集。
格
格是一个偏序集 $(L, \le)$,对于其中的每一对 $\lbrace a, b \rbrace \in L$,都存在最小上界(记作 $a \lor b$)和最大下界(记作 $a \land b$)。LUB $(\lbrace a, b \rbrace)$ 称为 a 和 b 的并。GLB $(\lbrace a, b \rbrace)$ 称为 a 和 b 的交。
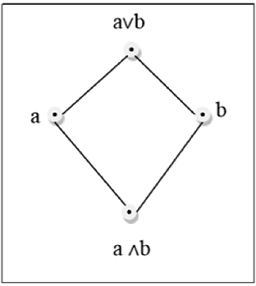
示例
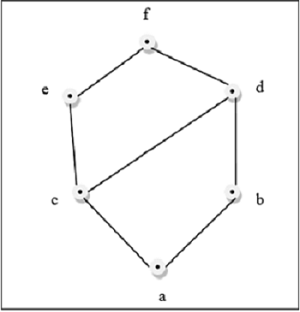
上图是一个格,因为对于每一对 $\lbrace a, b \rbrace \in L$,都存在 GLB 和 LUB。
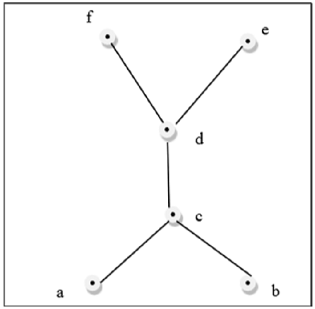
上图不是格,因为GLB(a, b)和LUB(e, f)不存在。
下面讨论其他一些格:
有界格
如果格L具有最大元1和最小元0,则L成为有界格。
补格
如果格L是有界格,并且格中的每个元素都有补元,则L成为补格。如果存在x’,满足x∧x’=0且x∨x’=1,则元素x的补元为x’。
分配格
如果格满足以下两个分配律,则称其为分配格。
a∨(b∧c) = (a∨b)∧(a∨c)
a∧(b∨c) = (a∧b)∨(a∧c)
模格
如果格满足以下性质,则称其为模格。
a∧(b∨(a∧d)) = (a∧b)∨(a∧d)
格的性质
幂等律
a∨a = a
a∧a = a
吸收律
a∨(a∧b) = a
a∧(a∨b) = a
交换律
a∨b = b∨a
a∧b = b∧a
结合律
a∨(b∨c) = (a∨b)∨c
a∧(b∧c) = (a∧b)∧c
格的对偶
格的对偶是通过互换'∨'和'∧'运算得到的。
示例
[a∨(b∧c)]的对偶是[a∧(b∨c)]
离散数学 - 计数理论
在日常生活中,很多时候需要找出一系列事件所有可能结果的数量。例如,从50名男性和38名女性中选出6名男性和4名女性组成的评审团有多少种方法?可以生成多少个不同的10位数的税务识别号(PAN),使得前五位是大写字母,接下来的四位是数字,最后一位又是大写字母?为了解决这些问题,使用了数学计数理论。**计数**主要包括基本计数规则、排列规则和组合规则。
加法和乘法规则
**加法规则**和**乘法规则**用于将复杂的计数问题分解成简单的子问题。
**加法规则** - 如果一系列任务T₁,T₂,…,Tₘ分别可以用w₁,w₂,…,wₘ种方式完成(条件是不能同时执行任务),那么完成其中一项任务的方法数是w₁+w₂+…+wₘ。如果我们考虑两个不相交的任务A和B(即A∩B=∅),那么数学上|A∪B|=|A|+|B|。
**乘法规则** - 如果一系列任务T₁,T₂,…,Tₘ分别可以用w₁,w₂,…,wₘ种方式完成,并且每个任务都在前一个任务发生后到达,那么完成这些任务的方法数为w₁×w₂×…×wₘ。数学上,如果任务B在任务A之后到达,那么|A×B|=|A|×|B|。
示例
**问题** - 一个男孩住在X,想去Z学校。他必须先从家X到达Y,然后从Y到达Z。他可以乘坐3条公交路线或2条火车路线从X到Y。从那里,他可以选择4条公交路线或5条火车路线到达Z。从X到Z有多少种方法?
**解答** - 从X到Y,他可以有3+2=5种方法(加法规则)。然后,他可以用4+5=9种方法从Y到Z(加法规则)。因此,从X到Z,他可以用5×9=45种方法(乘法规则)。
排列
**排列**是某些元素的一种排列,其中顺序很重要。换句话说,排列是元素的有序组合。
例子
从集合S={x, y, z}中每次取两个元素,所有排列为:
xy, yx, xz, zx, yz, zy。
我们必须从数字集合S={1, 2, 3}中构成三位数的排列。当我们排列数字时,将形成不同的三位数。排列将是:123, 132, 213, 231, 312, 321。
排列数
从n个不同事物中取r个的排列数记为ⁿPᵣ
$$n_{P_{r}} = \frac{n!}{(n - r)!}$$
其中n!=1.2.3… (n-1).n
**证明** - 假设有n个不同的元素。
有n种方法填补第一个位置。填补第一个位置后,剩下(n-1)个元素。因此,有(n-1)种方法填补第二个位置。填补第一和第二个位置后,剩下(n-2)个元素。因此,有(n-2)种方法填补第三个位置。现在我们可以将填补第r个位置的方法数推广为[n – (r–1)] = n–r+1
因此,从第一个位置到第r个位置的总方法数为:
ⁿPᵣ = n(n-1)(n-2)……(n-r+1)
=[n(n-1)(n-2)…(n-r+1)][(n-r)(n-r-1)…3.2.1]/[(n-r)(n-r-1)…3.2.1]
因此,
ⁿPᵣ = n!/(n-r)!
排列的一些重要公式
如果有n个元素,其中a₁个是某种类型的相同元素,a₂个是另一种类型的相同元素;a₃个是第三种类型的相同元素,以此类推,aᵣ个是第r种类型的相同元素,其中(a₁+a₂+…+aᵣ)=n。
那么,这n个对象的排列数为= n! / [(a₁!)(a₂!)…(aᵣ!)]。
从n个不同元素中取n个元素的排列数= ⁿPₙ = n!
从n个不同元素中取r个元素的排列数,当x个特定事物总是占据确定的位置= ⁿ⁻ˣPᵣ⁻ˣ
当r个指定事物总是放在一起时,n个不同元素的排列数为= r!(n−r+1)!
当r个指定事物从不放在一起时,n个不同元素的排列数为= n!–[r!(n−r+1)!]
从n个不同元素中取x个元素的环形排列数= ⁿPₓ/x
n个不同事物的环形排列数= ⁿPₙ/n
一些问题
**问题1** - 从一堆6张不同的卡片中,有多少种排列方法?
**解答** - 因为我们一次从6张卡片中取6张卡片,所以排列数为⁶P₆ = 6! = 720
**问题2** - 单词'READER'的字母有多少种排列方法?
**解答** - 单词'READER'有6个字母(2个E,1个A,1个D和2个R)。
排列数将是= 6! / [(2!)(1!)(1!)(2!)] = 180。
**问题3** - 单词'ORANGE'的字母有多少种排列方法,使得辅音只占据偶数位置?
**解答** - 单词'ORANGE'中有3个元音和3个辅音。辅音自身排列的方法数= ³P₃ = 3! = 6。剩下的3个空位将由3个元音以³P₃ = 3! = 6种方法填补。因此,排列总数为6 × 6 = 36
组合
**组合**是某些给定元素的选择,其中顺序无关紧要。
从n个事物中取r个的所有组合数为:
$$^nC_{r} = \frac{n!}{r!(n-r)!}$$
问题1
求集合{1, 2, 3, 4, 5, 6}中具有3个元素的子集的个数。
解答
集合的基数为6,我们必须从集合中选择3个元素。这里,顺序无关紧要。因此,子集的个数为⁶C₃ = 20。
问题2
一个房间里有6个男人和5个女人。从房间里选择3个男人和2个女人的方法有多少种?
解答
从6个男人中选择3个男人的方法数为⁶C₃,从5个女人中选择2个女人的方法数为⁵C₂。
因此,总方法数为:⁶C₃ × ⁵C₂ = 20 × 10 = 200
问题3
从总共9名学生中选择3个不同的3人小组有多少种方法?
解答
让我们将小组编号为1、2和3。
为第一个小组选择3名学生的方法数:⁹C₃
在选择第一个小组后,为第二个小组选择3名学生的方法数:⁶C₃
在选择第一个和第二个小组后,为第三个小组选择3名学生的方法数:³C₃
因此,总方法数= ⁹C₃ × ⁶C₃ × ³C₃ = 84 × 20 × 1 = 1680
帕斯卡恒等式
帕斯卡恒等式,由布莱斯·帕斯卡在17世纪首次推导出来,指出从n个元素中选择k个元素的方法数等于从(n-1)个元素中选择(k-1)个元素的方法数和从n-1个元素中选择k个元素的方法数之和。
数学上,对于任何正整数k和n:ⁿCₖ = ⁿ⁻¹Cₖ₋₁ + ⁿ⁻¹Cₖ
**证明**:
$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$
= (n-1)! / [(k-1)!(n-k)!] + (n-1)! / [k!(n-k-1)!]
= (n-1)! (k / [k!(n-k)!] + (n-k) / [k!(n-k)!])
= (n-1)! n / [k!(n-k)!]
= n! / [k!(n-k)!]
= ⁿCₖ
鸽巢原理
1834年,德国数学家彼得·古斯塔夫·勒热纳·狄利克雷提出一个他称之为抽屉原理的原理。现在,它被称为鸽巢原理。
**鸽巢原理**指出,如果鸽巢的数量少于鸽子的总数,并且每只鸽子都放在一个鸽巢中,那么必须至少有一个鸽巢中有多于一只鸽子。如果n只鸽子被放入m个鸽巢中,其中n>m,则至少有一个鸽巢中有多于一只鸽子。
例子
十个人在一个房间里互相握手。如果每个人至少握一次手,并且没有人与同一个人握手多次,那么有两名参与握手的人握手的次数相同。
在一个30人的班级里,至少有两名学生的名字以相同的字母开头。
容斥原理
容斥原理用于计算多个非互斥集合的并集的基数。对于两个集合A和B,该原理指出:
$|A \cup B| = |A| + |B| - |A \cap B|$
对于三个集合A,B和C,该原理指出:
$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$
推广公式:
$|\bigcup_{i=1}^{n}A_i|=\sum_{i=1}^{n}|A_i| - \sum\limits_{1\leq i<j\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\n-1}|A_1 \cap \dots \cap A_n|$
问题1
从1到50的整数中,有多少个是2或3的倍数,但不是两者兼有的倍数?
解答
从1到50,有$50/2 = 25$个数是2的倍数。
有$50/3 = 16$个数是3的倍数。
有$50/6 = 8$个数是2和3的倍数。
所以,$|A|=25$,$|B|=16$,$|A \cap B|= 8$。
$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$
问题2
在一个50名学生的群体中,24人喜欢冷饮,36人喜欢热饮,每个学生至少喜欢其中一种饮品。有多少人既喜欢咖啡又喜欢茶?
解答
设X为喜欢冷饮的学生集合,Y为喜欢热饮的学生集合。
所以,$| X \cup Y | = 50$,$|X| = 24$,$|Y| = 36$
$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 10$
因此,有10名学生既喜欢茶又喜欢咖啡。
离散数学 - 概率
与计数概念密切相关的是概率。我们经常试图猜测偶然事件的结果,例如纸牌游戏、老虎机和彩票;也就是说,我们试图找到获得特定结果的可能性或概率。
概率可以被概念化为寻找事件发生的机会。从数学上讲,它是对随机过程及其结果的研究。概率定律广泛应用于遗传学、天气预报、民意调查、股票市场等各种领域。
基本概念
概率论是由两位17世纪的法国数学家布莱兹·帕斯卡和皮埃尔·德·费马发明的,他们当时正在处理关于机会的数学问题。
在详细介绍概率之前,让我们先了解一些定义的概念。
随机试验- 在所有可能的结果已知且无法预先预测确切结果的实验称为随机试验。抛掷一枚公平的硬币就是一个随机试验的例子。
样本空间- 当我们进行实验时,所有可能结果的集合S称为样本空间。如果我们抛掷一枚硬币,样本空间$S = \left \{ H, T \right \}$
事件- 样本空间的任何子集都称为事件。抛掷硬币后,正面朝上就是一个事件。
“概率”一词意味着特定事件发生的可能性。我们最多只能说它们发生的可能性有多大,使用概率的概念。
$事件发生的概率 = \frac{有利结果的总数}{总结果数}$
由于任何事件的发生概率在0%到100%之间变化,因此概率在0到1之间变化。
计算概率的步骤
步骤1 - 计算实验的所有可能结果。
步骤2 - 计算实验的有利结果数。
步骤3 - 应用相应的概率公式。
抛掷硬币
如果抛掷一枚硬币,则有两个可能的结果 - 正面$(H)$或反面$(T)$
所以,总结果数 = 2
因此,正面$(H)$朝上的概率为1/2,反面$(T)$朝上的概率为1/2
掷骰子
当掷骰子时,顶部可能出现六个结果 - $1, 2, 3, 4, 5, 6$。
任何一个数字的概率是1/6
得到偶数的概率是3/6 = 1/2
得到奇数的概率是3/6 = 1/2
从一副牌中抽取扑克牌
从一副52张牌中,如果抽取一张牌,求抽到A的概率,以及求抽到方块的概率。
总可能结果数 - 52
抽到A的结果 - 4
抽到A的概率 = 4/52 = 1/13
抽到方块的概率 = 13/52 = 1/4
概率公理
事件的概率始终在0到1之间变化。$[0 \leq P(x) \leq 1]$
对于不可能发生的事件,概率为0;对于必然发生的事件,概率为1。
如果一个事件的发生不受另一个事件的影响,则它们被称为互斥事件或不相交事件。
如果$A_1, A_2....A_n$是互斥/不相交事件,则对于$i \ne j$,$P(A_i \cap A_j) = \emptyset $,并且$P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$
概率的性质
如果有两个互补事件x和$\overline{x}$,则互补事件的概率为:
$$p(\overline{x}) = 1-p(x)$$
对于两个非互斥事件A和B,两个事件并集的概率:
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
如果事件A是另一个事件B的子集(即$A \subset B$),则A的概率小于或等于B的概率。因此,$A \subset B$意味着$P(A) \leq p(B)$
条件概率
事件B的条件概率是在事件A已经发生的情况下事件B发生的概率。这写成$P(B|A)$。
数学上 - $ P(B|A) = P(A \cap B)/ P(A)$
如果事件A和B是互斥的,则事件A之后事件B的条件概率将是事件B的概率,即$P(B)$。
问题1
在一个国家,所有青少年中有50%拥有自行车,所有青少年中有30%拥有自行车和脚踏车。如果青少年拥有脚踏车,那么青少年拥有自行车的概率是多少?
解答
让我们假设A是青少年只拥有自行车的事件,B是青少年只拥有自行车的事件。
所以,根据题目给出的问题,$P(A) = 50/100 = 0.5$,$P(A \cap B) = 30/100 = 0.3$。
$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$
因此,在青少年拥有脚踏车的情况下,青少年拥有自行车的概率为60%。
问题2
在一个班级中,所有学生中有50%玩板球,所有学生中有25%玩板球和排球。如果学生玩板球,那么学生玩排球的概率是多少?
解答
让我们假设A是学生只玩板球的事件,B是学生只玩排球的事件。
所以,根据题目给出的问题,$P(A) = 50/100 =0.5$,$P(A \cap B) = 25/ 100 =0.25$。
$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$
因此,如果学生玩板球,那么学生玩排球的概率是50%。
问题3
有六台好的笔记本电脑和三台有缺陷的笔记本电脑混在一起。为了找到有缺陷的笔记本电脑,所有笔记本电脑都将随机逐一测试。在前两次挑选中找到两台有缺陷的笔记本电脑的概率是多少?
解答
设A为事件,我们在第一次测试中找到一台有缺陷的笔记本电脑;B为事件,我们在第二次测试中找到一台有缺陷的笔记本电脑。
因此,$P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$
贝叶斯定理
定理 - 如果A和B是两个互斥事件,其中$P(A)$是A的概率,$P(B)$是B的概率,$P(A | B)$是在B为真的情况下A的概率,$P(B | A)$是在A为真的情况下B的概率,则贝叶斯定理指出:
$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$
贝叶斯定理的应用
在样本空间的所有事件都是互斥事件的情况下。
在对于每个$A_i$,已知$P( A_i \cap B )$或已知$P( A_i )$和$P(B|A_i)$的情况下。
问题
考虑三个笔筒。第一个笔筒包含2支红笔和3支蓝笔;第二个笔筒有3支红笔和2支蓝笔;第三个笔筒有4支红笔和1支蓝笔。每个笔筒被选择的概率相等。如果随机抽取一支笔,那么它是红笔的概率是多少?
解答
设$A_i$为事件,即选择第i个笔筒。
这里,i = 1,2,3。
由于选择笔筒的概率相等,$P(A_i) = 1/3$
设B为事件,即抽到一支红笔。
在第一个笔筒的五支笔中选择一支红笔的概率为:
$P(B|A_1) = 2/5$
在第二个笔筒的五支笔中选择一支红笔的概率为:
$P(B|A_2) = 3/5$
在第三个笔筒的五支笔中选择一支红笔的概率为:
$P(B|A_3) = 4/5$
根据贝叶斯定理:
$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$
$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$
$= 3/5$
数学归纳法
数学归纳法是一种用于证明结果或为自然数建立陈述的技术。本部分通过各种示例说明此方法。
定义
数学归纳法是一种数学技术,用于证明某个陈述、公式或定理对于每个自然数都成立。
该技术包括两个步骤来证明一个陈述,如下所示:
步骤1(基础步骤) - 它证明该陈述对于初始值成立。
步骤2(归纳步骤) - 它证明如果该陈述对于第n次迭代(或数字n)成立,则它对于第(n+1)th次迭代(或数字n+1)也成立。
如何操作
步骤 1 − 考虑一个初始值,使得命题成立。需要证明该命题对于 n = 初始值成立。
步骤 2 − 假设该命题对于任意值 n = k 成立。然后证明该命题对于 n = k+1 成立。实际上,我们将 n = k+1 分成两部分,一部分是 n = k(已证明),然后尝试证明另一部分。
问题1
$3^n-1$ 是 2 的倍数,其中 n = 1, 2, ...
解答
步骤 1 − 对于 $n = 1, 3^1-1 = 3-1 = 2$,是 2 的倍数。
步骤 2 − 假设 $3^n-1$ 对于 $n=k$ 成立,因此,$3^k -1$ 成立(这是一个假设)
我们需要证明 $3^{k+1}-1$ 也是 2 的倍数。
$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$
第一部分 $(2 \times 3^k)$ 必定是 2 的倍数,第二部分 $(3^k -1)$ 根据之前的假设也成立。
因此,$3^{k+1} – 1$ 是 2 的倍数。
所以,已证明 $3^n – 1$ 是 2 的倍数。
问题2
$1 + 3 + 5 + ... + (2n-1) = n^2$,其中 $n = 1, 2, \dots $
解答
步骤 1 − 对于 $n=1, 1 = 1^2$,因此,步骤 1 成立。
步骤 2 − 假设该命题对于 $n=k$ 成立。
因此,$1 + 3 + 5 + \dots + (2k-1) = k^2$ 成立(这是一个假设)
我们需要证明 $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ 也成立。
$1 + 3 + 5 + \dots + (2(k+1) - 1)$
$= 1 + 3 + 5 + \dots + (2k+2 - 1)$
$= 1 + 3 + 5 + \dots + (2k + 1)$
$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$
$= k^2 + (2k + 1)$
$= (k + 1)^2$
所以,$1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ 成立,满足步骤 2。
因此,已证明 $1 + 3 + 5 + \dots + (2n - 1) = n^2$。
问题3
证明 $(ab)^n = a^nb^n$ 对于任何自然数 n 都成立。
解答
步骤 1 − 对于 $n=1, (ab)^1 = a^1b^1 = ab$,因此,步骤 1 成立。
步骤 2 − 假设该命题对于 $n=k$ 成立,因此,$(ab)^k = a^kb^k$ 成立(这是一个假设)。
我们需要证明 $(ab)^{k+1} = a^{k+1}b^{k+1}$ 也成立。
已知,$(ab)^k = a^k b^k$
即, $(ab)^k (ab) = (a^k b^k ) (ab)$ [两边乘以 'ab']
即, $(ab)^{k+1} = (aa^k) ( bb^k)$
即, $(ab)^{k+1} = (a^{k+1}b^{k+1})$
因此,步骤 2 得证。
所以,$(ab)^n = a^nb^n$ 对于任何自然数 n 都成立。
强归纳法
强归纳法是数学归纳法的另一种形式。通过这种归纳技术,我们可以使用以下步骤证明命题函数 $P(n)$ 对于所有正整数 $n$ 都成立:
步骤 1(基础步骤) − 证明初始命题 $P(1)$ 成立。
步骤 2(归纳步骤) − 证明条件语句 $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ 对于正整数 $k$ 成立。
离散数学 - 递推关系
本章将讨论递归技术如何推导出序列并用于解决计数问题。以递归方式查找序列项的过程称为递推关系。我们将学习线性递推关系及其解的理论。最后,我们将介绍用于求解递推关系的生成函数。
定义
递推关系是一个递归定义序列的方程,其中下一项是前面各项的函数(将 $F_n$ 表示为 $i < n$ 的 $F_i$ 的某种组合)。
示例 − 斐波那契数列 − $F_n = F_{n-1} + F_{n-2}$,汉诺塔 − $F_n = 2F_{n-1} + 1$
线性递推关系
k 次或 k 阶线性递推方程是一个递推方程,其格式为 $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k}$($A_n$ 是常数,且 $A_k \neq 0$),它将数列表示为一阶多项式。
以下是一些线性递推方程的示例:
| 递推关系 | 初始值 | 解 |
|---|---|---|
| Fn = Fn-1 + Fn-2 | a1 = a2 = 1 | 斐波那契数 |
| Fn = Fn-1 + Fn-2 | a1 = 1, a2 = 3 | 卢卡斯数 |
| Fn = Fn-2 + Fn-3 | a1 = a2 = a3 = 1 | 帕多万数列 |
| Fn = 2Fn-1 + Fn-2 | a1 = 0, a2 = 1 | 佩尔数 |
如何求解线性递推关系
假设,一个二阶线性递推关系为 − $F_n = AF_{n-1} +BF_{n-2}$,其中 A 和 B 为实数。
上述递推关系的特征方程为 −
$$x^2 - Ax - B = 0$$
求根时可能出现三种情况:
情况 1 − 如果该方程可分解为 $(x- x_1)(x- x_1) = 0$,并产生两个不同的实根 $x_1$ 和 $x_2$,则 $F_n = ax_1^n+ bx_2^n$ 为解。[此处,a 和 b 为常数]
情况 2 − 如果该方程可分解为 $(x- x_1)^2 = 0$,并产生单个实根 $x_1$,则 $F_n = a x_1^n+ bn x_1^n$ 为解。
情况 3 − 如果该方程产生两个不同的复根 $x_1$ 和 $x_2$,其极坐标形式为 $x_1 = r \angle \theta$ 和 $x_2 = r \angle(- \theta)$,则 $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ 为解。
问题1
求解递推关系 $F_n = 5F_{n-1} - 6F_{n-2}$,其中 $F_0 = 1$ 和 $F_1 = 4$
解答
递推关系的特征方程为 −
$$x^2 - 5x + 6 = 0,$$
所以 $(x - 3) (x - 2) = 0$
因此,根为 −
$x_1 = 3$ 和 $x_2 = 2$
根为实数且不相等。所以,这属于情况 1。
因此,解为 −
$$F_n = ax_1^n + bx_2^n$$
此处,$F_n = a3^n + b2^n\ (因为\ x_1 = 3\ 且\ x_2 = 2)$
因此,
$1 = F_0 = a3^0 + b2^0 = a+b$
$4 = F_1 = a3^1 + b2^1 = 3a+2b$
求解这两个方程,我们得到 $ a = 2$ 和 $b = -1$
因此,最终解为 −
$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$
问题2
求解递推关系 − $F_n = 10F_{n-1} - 25F_{n-2}$,其中 $F_0 = 3$ 和 $F_1 = 17$
解答
递推关系的特征方程为 −
$$ x^2 - 10x -25 = 0$$
所以 $(x - 5)^2 = 0$
因此,存在单个实根 $x_1 = 5$
由于存在单个实数根,这属于情况 2。
因此,解为 −
$F_n = ax_1^n + bnx_1^n$
$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$
$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$
求解这两个方程,我们得到 $a = 3$ 和 $b = 2/5$
因此,最终解为 − $F_n = 3.5^n +( 2/5) .n.2^n $
问题3
求解递推关系 $F_n = 2F_{n-1} - 2F_{n-2}$,其中 $F_0 = 1$ 和 $F_1 = 3$
解答
递推关系的特征方程为 −
$$x^2 -2x -2 = 0$$
因此,根为 −
$x_1 = 1 + i$ 和 $x_2 = 1 - i$
以极坐标形式表示,
$x_1 = r \angle \theta$ 和 $x_2 = r \angle(- \theta)$,其中 $r = \sqrt 2$ 和 $\theta = \frac{\pi}{4}$
根为虚数。所以,这属于情况 3。
因此,解为 −
$F_n = (\sqrt 2 )^n (a cos(n .\pi /4) + b sin(n .\pi /4))$
$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\pi /4) + b sin(0 .\pi /4) ) = a$
$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\pi /4) + b sin(1 . \pi /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$
求解这两个方程,我们得到 $a = 1$ 和 $b = 2$
因此,最终解为 −
$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$
非齐次递推关系和特解
如果递推关系的形式为
$F_n = AF_{n-1} + BF_{n-2} + f(n)$,其中 $f(n) \ne 0$,则该递推关系称为非齐次递推关系。
其相关的齐次递推关系为 $F_n = AF_{n–1} + BF_{n-2}$
非齐次递推关系的解 $(a_n)$ 包含两部分。
第一部分是相关齐次递推关系的解 $(a_h)$,第二部分是特解 $(a_t)$。
$$a_n=a_h+a_t$$
第一部分的解法在上一节中已讨论。
为了找到特解,我们找到一个合适的试验解。
令 $f(n) = cx^n$;令 $x^2 = Ax + B$ 为相关齐次递推关系的特征方程,并令 $x_1$ 和 $x_2$ 为其根。
如果 $x \ne x_1$ 且 $x \ne x_2$,则 $a_t = Ax^n$
如果 $x = x_1$,$x \ne x_2$,则 $a_t = Anx^n$
如果 $x = x_1 = x_2$,则 $a_t = An^2x^n$
示例
令非齐次递推关系为 $F_n = AF_{n–1} + BF_{n-2} + f(n)$,其特征根为 $x_1 = 2$ 和 $x_2 = 5$。对于 $f(n)$ 的不同可能值,试验解如下: