
- 离散数学资源
- 离散数学 - 快速指南
- 离散数学 - 资源
- 离散数学 - 讨论
离散数学 - 图论进阶
图着色
图着色是指为图 G 的每个顶点分配颜色的过程,使得没有相邻的顶点具有相同的颜色。目标是在着色图时最小化颜色的数量。为着色图 G 所需的最少颜色数称为该图的色数。图着色问题是一个 NP 完全问题。
图着色方法
为具有 n 个顶点的图 G 着色的步骤如下:
步骤 1 - 按某种顺序排列图的顶点。
步骤 2 - 选择第一个顶点并用第一种颜色对其进行着色。
步骤 3 - 选择下一个顶点,并用与其相邻的任何顶点都没有着色的最低编号的颜色对其进行着色。如果所有相邻顶点都用此颜色着色,则为其分配一个新颜色。重复此步骤,直到所有顶点都着色。
示例
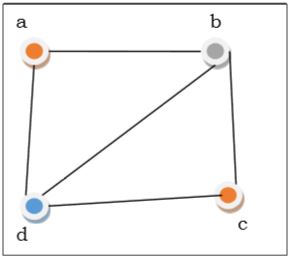
在上图中,首先将顶点 $a$ 着色为红色。由于顶点 a 的相邻顶点再次相邻,因此顶点 $b$ 和顶点 $d$ 用不同的颜色着色,分别为绿色和蓝色。然后将顶点 $c$ 着色为红色,因为 $c$ 的任何相邻顶点都没有着色为红色。因此,我们可以用 3 种颜色对图进行着色。因此,该图的色数为 3。
图着色的应用
图着色的一些应用包括:
图遍历
图遍历是按照某种系统顺序访问图的所有顶点的问题。主要有两种遍历图的方法。
- 广度优先搜索
- 深度优先搜索
广度优先搜索
广度优先搜索 (BFS) 从图 $G$ 的起始层级 0 顶点 $X$ 开始。然后我们访问 $X$ 的所有邻居顶点。访问后,我们将顶点标记为“已访问”,并将它们放入层级 1。然后我们从层级 1 顶点开始,对每个层级 1 顶点应用相同的方法,依此类推。当图的每个顶点都被访问后,BFS 遍历终止。
BFS 算法
其概念是在访问邻居顶点的其他邻居顶点之前访问所有邻居顶点。
将所有节点的状态初始化为“就绪”。
将源顶点放入队列中,并将状态更改为“等待”。
重复以下两个步骤,直到队列为空:
从队列中删除第一个顶点,并将其标记为“已访问”。
将状态为“就绪”的已删除顶点的所有邻居添加到队列的尾部。将其状态标记为“等待”。
问题
让我们取一个图(源顶点为“a”),并应用 BFS 算法找出遍历顺序。
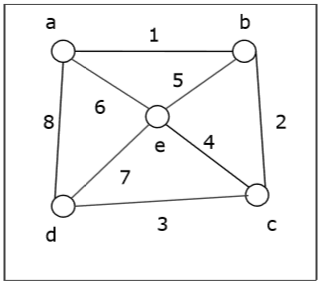
解决方案 -
将所有顶点状态初始化为“就绪”。
将 a 放入队列中,并将状态更改为“等待”。
从队列中删除 a,将其标记为“已访问”。
将 a 的状态为“就绪”的邻居 b、d 和 e 添加到队列的末尾,并将它们标记为“等待”。
从队列中删除 b,将其标记为“已访问”,将状态为“就绪”的邻居 c 放入队列的末尾,并将 c 标记为“等待”。
从队列中删除 d,并将其标记为“已访问”。它没有状态为“就绪”的邻居。
从队列中删除 e,并将其标记为“已访问”。它没有状态为“就绪”的邻居。
从队列中删除 c,并将其标记为“已访问”。它没有状态为“就绪”的邻居。
队列为空,因此停止。
因此,遍历顺序为:
$a \rightarrow b \rightarrow d \rightarrow e \rightarrow c$
遍历的替代顺序为:
$a \rightarrow b \rightarrow e \rightarrow d \rightarrow c$
或者,$a \rightarrow d \rightarrow b \rightarrow e \rightarrow c$
或者,$a \rightarrow e \rightarrow b \rightarrow d \rightarrow c$
或者,$a \rightarrow b \rightarrow e \rightarrow d \rightarrow c$
或者,$a \rightarrow d \rightarrow e \rightarrow b \rightarrow c$
BFS 的应用
- 查找最短路径
- 无权图的最小生成树
- GPS 导航系统
- 检测无向图中的循环
- 查找一个连通分量内的所有节点
复杂度分析
令 $G(V, E)$ 为一个具有 $|V|$ 个顶点和 $|E|$ 条边的图。如果广度优先搜索算法访问图中的每个顶点并检查每条边,则其时间复杂度为:
$$O( | V | + | E | ). O( | E | )$$
它可能在 $O(1)$ 和 $O(|V2|)$ 之间变化
深度优先搜索
深度优先搜索 (DFS) 算法从顶点 $v$ 开始,然后遍历到其之前未访问过的相邻顶点(例如 x),并将其标记为“已访问”,然后继续遍历 x 的相邻顶点,依此类推。
如果在任何顶点处遇到所有相邻顶点都已访问,则它会回溯,直到找到第一个具有未遍历过的相邻顶点的顶点。然后,它遍历该顶点,继续遍历其相邻顶点,直到遍历所有已访问的顶点并且必须再次回溯。通过这种方式,它将遍历从初始顶点 $v$ 可到达的所有顶点。
DFS 算法
其概念是在访问邻居顶点的其他邻居顶点之前访问所有邻居顶点。
将所有节点的状态初始化为“就绪”
将源顶点放入堆栈中,并将状态更改为“等待”
重复以下两个步骤,直到堆栈为空:
从堆栈中弹出顶部的顶点,并将其标记为“已访问”
将状态为“就绪”的已删除顶点的所有邻居推送到堆栈的顶部。将其状态标记为“等待”。
问题
让我们取一个图(源顶点为“a”),并应用 DFS 算法找出遍历顺序。
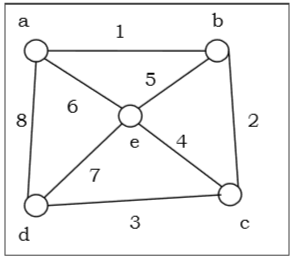
解决方案
将所有顶点状态初始化为“就绪”。
将 a 推入堆栈中,并将状态更改为“等待”。
弹出 a 并将其标记为“已访问”。
将 a 的状态为“就绪”的邻居 e、d 和 b 推送到堆栈的顶部,并将它们标记为“等待”。
从堆栈中弹出 b,将其标记为“已访问”,将状态为“就绪”的邻居 c 推送到堆栈中。
从堆栈中弹出 c 并将其标记为“已访问”。它没有“就绪”的邻居。
从堆栈中弹出 d 并将其标记为“已访问”。它没有“就绪”的邻居。
从堆栈中弹出 e 并将其标记为“已访问”。它没有“就绪”的邻居。
堆栈为空。因此停止。
因此,遍历顺序为:
$a \rightarrow b \rightarrow c \rightarrow d \rightarrow e$
遍历的替代顺序为:
$a \rightarrow e \rightarrow b \rightarrow c \rightarrow d$
或者,$a \rightarrow b \rightarrow e \rightarrow c \rightarrow d$
或者,$a \rightarrow d \rightarrow e \rightarrow b \rightarrow c$
或者,$a \rightarrow d \rightarrow c \rightarrow e \rightarrow b$
或者,$a \rightarrow d \rightarrow c \rightarrow b \rightarrow e$
复杂度分析
令 $G(V, E)$ 为一个具有 $|V|$ 个顶点和 $|E|$ 条边的图。如果 DFS 算法访问图中的每个顶点并检查每条边,则时间复杂度为:
$$\circleddash ( | V | + | E | )$$
应用
- 检测图中的循环
- 查找拓扑排序
- 测试图是否为二分图
- 查找连通分量
- 查找图的桥
- 查找图中的双连通性
- 解决骑士巡游问题
- 解决只有一个解决方案的谜题