
- 离散数学资源
- 离散数学 - 快速指南
- 离散数学 - 资源
- 离散数学 - 讨论
离散数学 - 生成树
连通无向图 $G$ 的生成树是指包含 $G$ 中所有顶点的最小连通子图。一个图可能有多个生成树。
示例
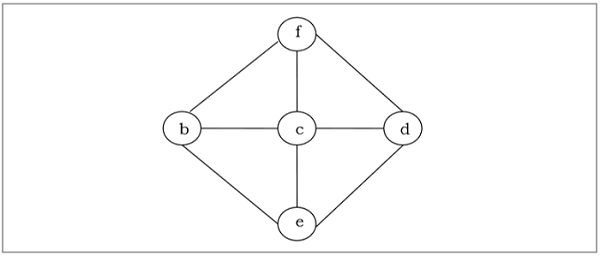
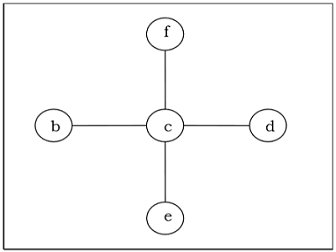
最小生成树
对于一个加权的、连通的、无向图 $G$,如果一个生成树的权重小于或等于该图所有可能的生成树的权重,则称之为最小生成树 (MST)。生成树的权重是指生成树中所有边的权重之和。
示例
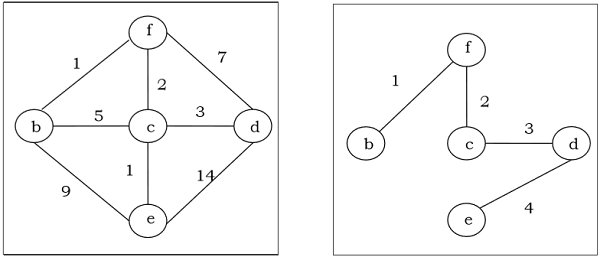
克鲁斯卡尔算法
克鲁斯卡尔算法是一种贪心算法,用于寻找连通加权图的最小生成树。它找到该图中包含每个顶点的树,并且树中所有边的总权重小于或等于所有可能的生成树。
算法
步骤 1 - 将给定图 $G (V,E)$ 的所有边按其边权重升序排列。
步骤 2 - 从图中选择权重最小的边,并检查它是否与迄今为止形成的生成树构成环。
步骤 3 - 如果没有环,则将此边包含到生成树中,否则丢弃它。
步骤 4 - 重复步骤 2 和步骤 3,直到生成树中剩下 $(V-1)$ 条边。
问题
假设我们想使用克鲁斯卡尔算法为以下图 G 找到最小生成树。
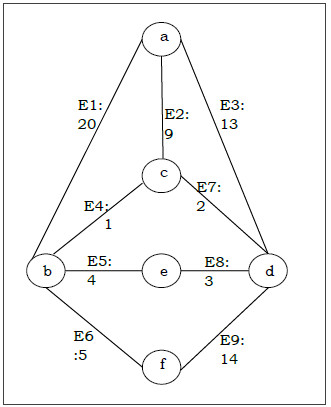
解决方案
根据上图,我们构建以下表格 -
| 边号 | 顶点对 | 边权重 |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E4 | (b, c) | 1 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
现在我们将表格根据边权重升序重新排列 -
| 边号 | 顶点对 | 边权重 |
|---|---|---|
| E4 | (b, c) | 1 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
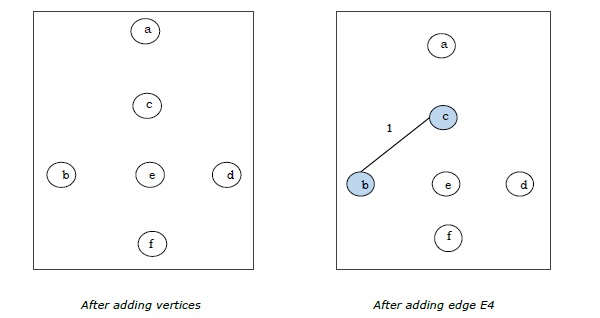
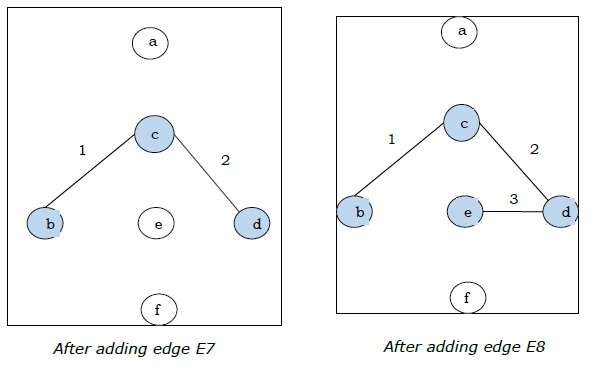
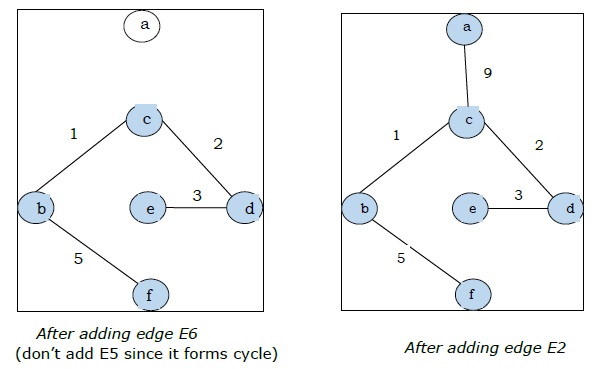
由于我们在上图中得到了所有 5 条边,因此我们停止算法,这就是最小生成树,其总权重为 $(1 + 2 + 3 + 5 + 9) = 20$。
普里姆算法
普里姆算法由数学家沃伊捷赫·亚尔尼克和罗伯特·C·普里姆于 1930 年发现,是一种贪心算法,用于寻找连通加权图的最小生成树。它找到该图中包含每个顶点的树,并且树中所有边的总权重小于或等于所有可能的生成树。普里姆算法在稠密图上速度更快。
算法
用从图中随机选择的单个顶点初始化最小生成树。
重复步骤 3 和 4,直到所有顶点都被包含在树中。
选择一条连接树与尚未在树中的顶点的边,使得边的权重最小,并且边的包含不会形成环。
将所选边及其连接到的顶点添加到树中。
问题
假设我们想使用普里姆算法为以下图 G 找到最小生成树。
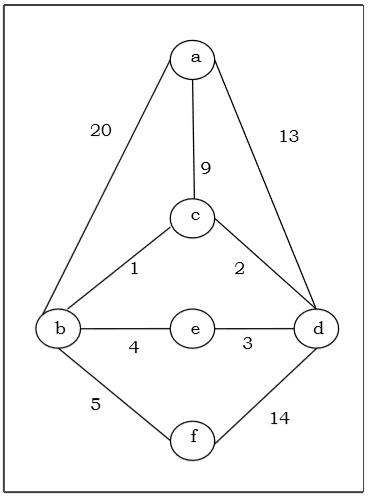
解决方案
这里我们从顶点 'a' 开始并继续。
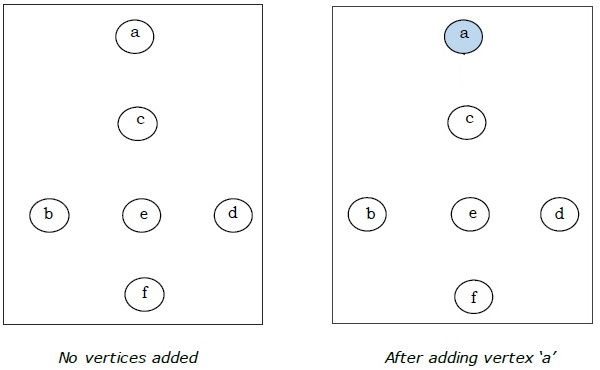
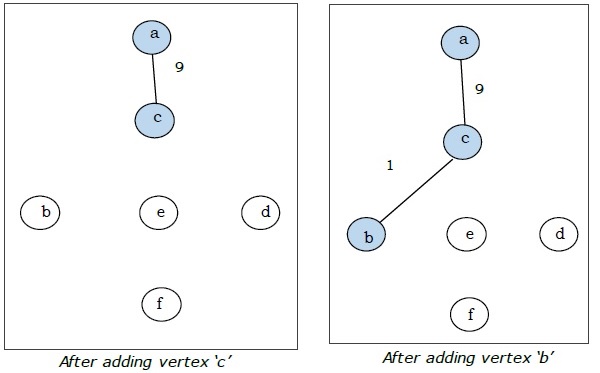
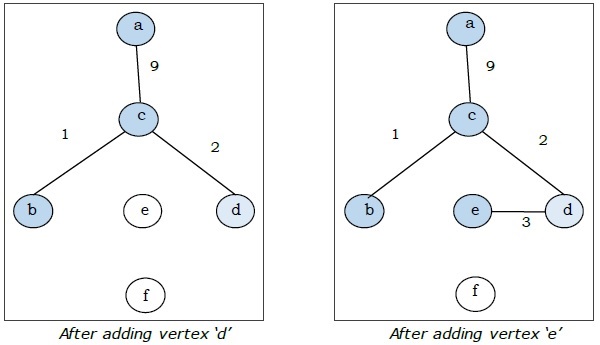
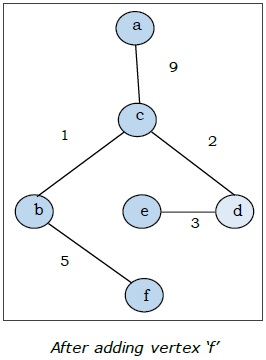
这是最小生成树,其总权重为 $(1 + 2 + 3 + 5 + 9) = 20$。