离散数学 - 关系

每当讨论集合时，集合元素之间的关系就是接下来要讨论的内容。**关系**可能存在于同一集合的对象之间，或者存在于两个或多个集合的对象之间。

定义和性质

从集合 x 到集合 y 的二元关系 R（写成 $xRy$ 或 $R(x,y)$）是笛卡尔积 $x \times y$ 的一个子集。如果 G 的有序对反转，关系也会发生变化。

通常，集合 $A_1, \dots ,\ and\ A_n$ 之间的 n 元关系 R 是 n 元积 $A_1 \times \dots \times A_n$ 的一个子集。在这种情况下，关系 R 的最小基数为零，最大基数为 $n^2$。

单个集合 A 上的二元关系 R 是 $A \times A$ 的一个子集。

对于两个不同的集合 A 和 B，分别具有基数 m 和 n，从 A 到 B 的关系 R 的最大基数为 mn。

域和范围

如果有两个集合 A 和 B，并且关系 R 有序对 (x, y)，则 -

• R 的**域** Dom(R) 是集合 $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$

• R 的**范围** Ran(R) 是集合 $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$

示例

令，$A = \lbrace 1, 2, 9 \rbrace $ 和 $ B = \lbrace 1, 3, 7 \rbrace$

• 情况 1 - 如果关系 R 是“等于”，则 $R = \lbrace (1, 1), (3, 3) \rbrace$

  Dom(R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$

• 情况 2 - 如果关系 R 是“小于”，则 $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$

  Dom(R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$

• 情况 3 - 如果关系 R 是“大于”，则 $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$

  Dom(R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$

使用图表示关系

关系可以使用有向图来表示。

图中顶点的数量等于定义关系的集合中元素的数量。对于关系 R 中的每个有序对 (x, y)，从顶点“x”到顶点“y”将有一条有向边。如果存在有序对 (x, x)，则顶点“x”上将有一个自环。

假设，在集合 $S = \lbrace 1, 2, 3 \rbrace$ 上存在一个关系 $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$，它可以用下图表示 -

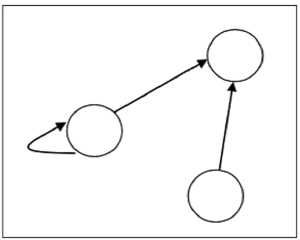
关系的类型

• 集合 X 和 Y 之间或集合 E 上的**空关系**是空集 $\emptyset$

• 集合 X 和 Y 之间的**全关系**是集合 $X \times Y$

• 集合 X 上的**恒等关系**是集合 $\lbrace (x, x) | x \in X \rbrace$

• 关系 R 的逆关系 R' 定义为 - $R' = \lbrace (b, a) | (a, b) \in R \rbrace$

  **示例** - 如果 $R = \lbrace (1, 2), (2, 3) \rbrace$，则 $R'$ 将是 $\lbrace (2, 1), (3, 2) \rbrace$

• 如果 $\forall a \in A$ 与 a 相关（aRa 成立），则称集合 A 上的关系 R 为**自反**的。

  **示例** - 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, a), (b, b) \rbrace$ 是自反的。

• 如果不存在 $a \in A$ 与 a 相关（aRa 不成立），则称集合 A 上的关系 R 为**反自反**的。

  **示例** - 集合 $X = \lbrace a, b \rbrace$ 上的关系 $R = \lbrace (a, b), (b, a) \rbrace$ 是反自反的。

• 如果 $xRy$ 意味着 $yRx$，$\forall x \in A$ 和 $\forall y \in A$，则称集合 A 上的关系 R 为**对称**的。

  **示例** - 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ 是对称的。

• 如果 $xRy$ 和 $yRx$ 意味着 $x = y \: \forall x \in A$ 和 $\forall y \in A$，则称集合 A 上的关系 R 为**反对称**的。

  **示例** - 关系 $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ 是反对称的，因为 $x \leq y$ 和 $y \leq x$ 意味着 $x = y$。

• 如果 $xRy$ 和 $yRz$ 意味着 $xRz, \forall x,y,z \in A$，则称集合 A 上的关系 R 为**传递**的。

  **示例** - 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ 是传递的。

• 如果关系是自反的、对称的和传递的，则它是**等价关系**。

  **示例** - 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的关系 $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ 是等价关系，因为它自反、对称和传递。