
- 离散数学资源
- 离散数学 - 快速指南
- 离散数学 - 资源
- 离散数学 - 讨论
布尔函数化简
使用代数函数化简
在这种方法中,一个布尔表达式通过应用布尔恒等式简化为一个等价的表达式。
问题 1
使用布尔恒等式最小化以下布尔表达式:
$$F (A, B, C) = A'B + BC'+ BC + AB'C'$$
解答
已知,$F (A, B, C) = A'B + BC'+ BC + AB'C'$
或,$F (A, B, C) = A'B + (BC'+ BC') + BC+ AB'C'$
[根据幂等律,BC’ = BC’ + BC’]
或,$F (A, B, C) = A'B + (BC'+ BC) + (BC'+ AB'C')$
或,$F (A, B, C) = A'B + B(C'+ C) + C'(B+ AB')$
[根据分配律]
或,$F (A, B, C) = A'B + B.1 + C'(B + A)$
[ (C' + C) = 1 且吸收律 (B + AB')= (B + A)]
或,$F (A, B, C) = A'B + B + C'(B + A)$
[ B.1 = B ]
或,$F (A, B, C) = B(A'+ 1) + C'(B + A)$
或,$F (A, B, C) = B.1 + C'(B + A)$
[ (A' + 1) = 1 ]
或,$F (A, B, C) = B + C'(B + A)$
[ 因为,B.1 = B ]
或,$F (A, B, C) = B + BC' + AC'$
或,$F (A, B, C) = B(1 + C') + AC'$
或,$F (A, B, C) = B.1 + AC'$
[因为,(1 + C') = 1]
或,$F (A, B, C) = B + AC'$
[因为,B.1 = B]
所以,$F (A, B, C) = B + AC'$是最小化形式。
问题 2
使用布尔恒等式最小化以下布尔表达式:
$$F (A, B, C) = (A + B) (A + C)$$
解答
已知,$F (A, B, C) = (A + B) (A + C)$
或,$F (A, B, C) = A.A + A.C + B.A + B.C$ [应用分配律]
或,$F (A, B, C) = A + A.C + B.A + B.C$ [应用幂等律]
或,$F (A, B, C) = A(1 + C) + B.A + B.C$ [应用分配律]
或,$F (A, B, C) = A + B.A + B.C$ [应用支配律]
或,$F (A, B, C) = (A + 1).A + B.C$ [应用分配律]
或,$F (A, B, C) = 1.A + B.C$ [应用支配律]
或,$F (A, B, C) = A + B.C$ [应用支配律]
所以,$F (A, B, C) = A + BC$ 是最小化形式。
卡诺图
卡诺图(K-map),由 Maurice Karnaugh 于 1953 年提出,是真值表的网格状表示,用于简化布尔代数表达式。卡诺图在不同位置具有 0 和 1 的条目。它将具有公共因子的布尔表达式组合在一起,并从表达式中消除不需要的变量。在 K-map 中,跨越垂直或水平单元格边界总是仅改变一个变量。
示例 1
下面给出了一个任意的真值表:
| A | B | A 操作 B |
|---|---|---|
| 0 | 0 | w |
| 0 | 1 | x |
| 1 | 0 | y |
| 1 | 1 | z |
现在我们将为上述真值表创建一个 K-map:
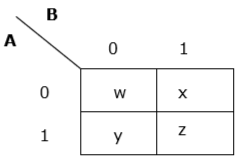
示例 2
现在我们将为表达式 AB+ A’B’ 创建一个 K-map:
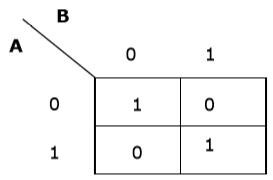
使用 K-map 化简
K-map 使用一些规则通过将相邻单元格组合成单个项来简化布尔表达式。规则如下:
规则 1 - 任何包含零的单元格都不能分组。
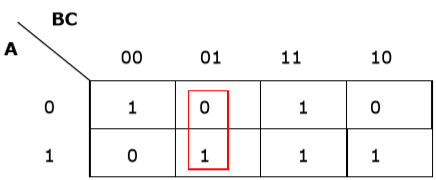
错误分组
规则 2 - 组必须包含 2n 个单元格(n 从 1 开始)。
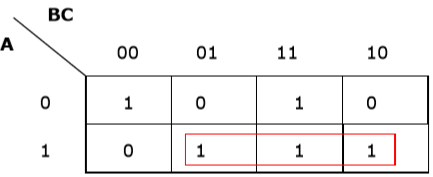
错误分组
规则 3 - 分组必须是水平或垂直的,但不能是对角线的。
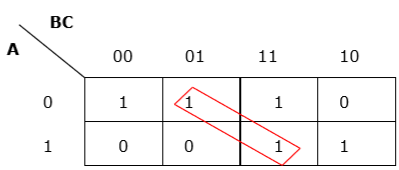
错误的对角线分组
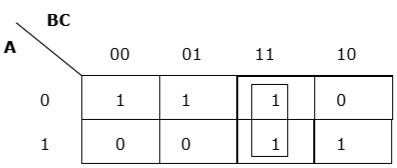
正确的垂直分组
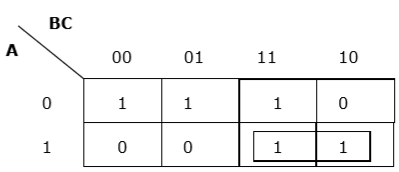
正确的水平分组
规则 4 - 组必须尽可能大。
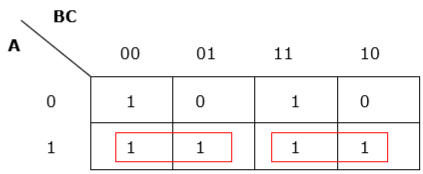
分组不足
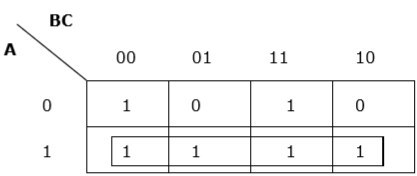
正确分组
规则 5 - 如果任何单元格的 1 不能与任何其他单元格分组,它将本身作为一个组。
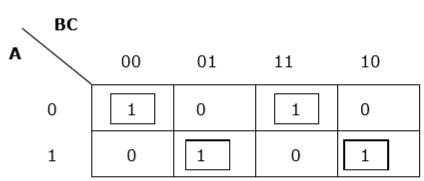
正确分组
规则 6 - 组可以重叠,但组的数量应尽可能少。
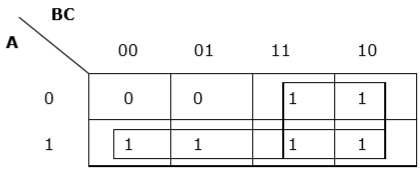
正确分组
规则 7 - 最左侧的单元格/单元格可以与最右侧的单元格/单元格分组,最顶部的单元格/单元格可以与最底部的单元格/单元格分组。
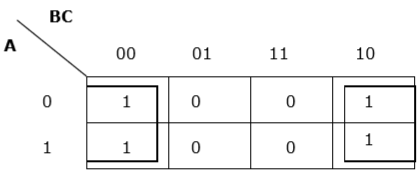
正确分组
问题
使用 K-map 最小化以下布尔表达式:
$$F (A, B, C) = A'BC + A'BC' + AB'C'+ AB'C$$
解答
每个项都放入 K-map 中,我们得到以下结果:
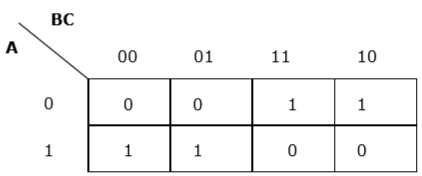
F (A, B, C) 的 K-map
现在我们将根据上面列出的规则对 1 的单元格进行分组:
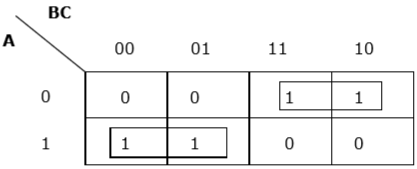
F (A, B, C) 的 K-map
我们得到了两个组,称为 $A’B$ 和 $AB’$。因此,$F (A, B, C) = A’B+ AB’= A \oplus B$。这是最小化形式。