- 离散数学资源
- 离散数学 - 快速指南
- 离散数学 - 资源
- 离散数学 - 讨论
图与图模型
上一部分介绍了推理、证明和解决问题的不同工具。在本部分中,我们将学习构成许多现实生活问题基础的离散结构。
我们将介绍的两种离散结构是图和树。图是由称为节点或顶点的点集以及由称为边的线集相互连接而成的。图的研究,或图论,是数学、工程和计算机科学领域许多学科的重要组成部分。
什么是图?
定义 − 图(表示为$G = (V, E)$)由非空顶点集或节点集 V 和边集 E 组成。
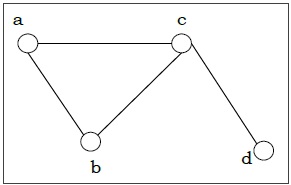
示例 − 让我们考虑一个图$G = (V, E)$,其中$V = \lbrace a, b, c, d \rbrace$,而$E = \lbrace \lbrace a, b \rbrace, \lbrace a, c \rbrace, \lbrace b, c \rbrace, \lbrace c, d \rbrace \rbrace$
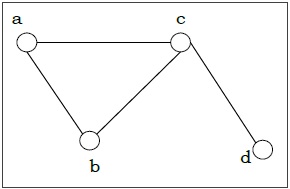
顶点的度 − 图 G 的顶点 V 的度(用 deg (V) 表示)是与顶点 V 相连的边的数量。
| 顶点 | 度 | 偶数/奇数 |
|---|---|---|
| a | 2 | 偶数 |
| b | 2 | 偶数 |
| c | 3 | 奇数 |
| d | 1 | 奇数 |
偶数顶点和奇数顶点 − 如果顶点的度为偶数,则该顶点称为偶数顶点;如果顶点的度为奇数,则该顶点称为奇数顶点。
图的度 − 图的度是该图中最大的顶点度。对于上述图,图的度为 3。
握手引理 − 在一个图中,所有顶点的度之和等于边数的两倍。
图的类型
在下一节中,我们将学习不同类型的图。
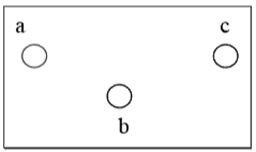
空图
空图没有边。n 个顶点的空图用 $N_n$ 表示。
简单图
如果图是无向的并且不包含任何环或多重边,则该图称为简单图/严格图。
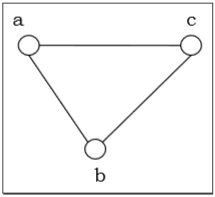
多重图
如果允许图中同一组顶点之间存在多条边,则称其为多重图。换句话说,它是一个至少包含一个环或多重边的图。
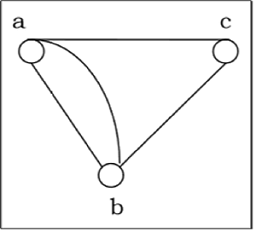
有向图和无向图
如果边集由有序顶点对组成,则图 $G = (V, E)$ 称为有向图;如果边集由无序顶点对组成,则图称为无向图。
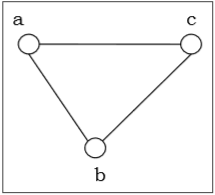
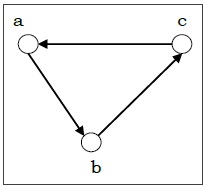
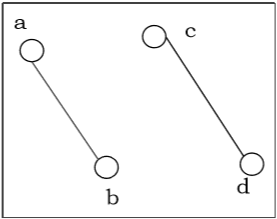
连通图和非连通图
如果图的任意两个顶点都由一条路径连接,则该图是连通的;如果图中至少有两个顶点不能由路径连接,则该图是非连通的。如果图 G 是非连通的,则 G 的每个最大连通子图都称为图 G 的连通分量。
正则图
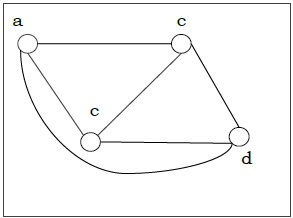
如果图的所有顶点都具有相同的度,则该图是正则图。在度为 r 的正则图 G 中,G 的每个顶点的度都为 r。
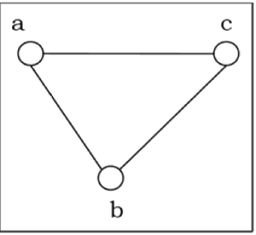
完全图
如果每对顶点都恰好由一条边连接,则该图称为完全图。具有 n 个顶点的完全图用 $K_n$ 表示。
环图
如果一个图由一个单一的环组成,则它被称为环图。具有 n 个顶点的环图用 $C_n$ 表示。
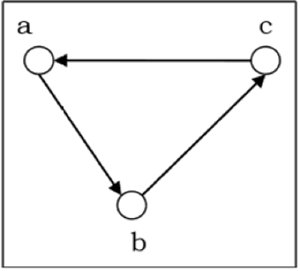
二分图
如果图 G 的顶点集可以分成两个不相交的集合 $V_1$ 和 $V_2$,以使图中的每条边都连接 $V_1$ 中的一个顶点和 $V_2$ 中的一个顶点,并且 G 中没有边连接 $V_1$ 中的两个顶点或 $V_2$ 中的两个顶点,则图 G 称为二分图。
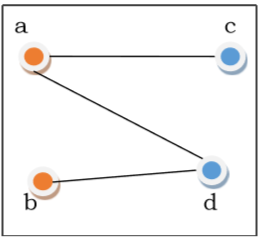
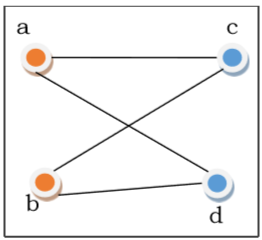
完全二分图
完全二分图是一个二分图,其中第一组中的每个顶点都与第二组中的每个顶点连接。完全二分图用 $K_{x,y}$ 表示,其中图 G 在第一组中有 x 个顶点,在第二组中有 y 个顶点。
图的表示
主要有两种表示图的方法:
- 邻接矩阵
- 邻接表
邻接矩阵
邻接矩阵 $A[V][V]$ 是一个大小为 $V \times V$ 的二维数组,其中 V 是无向图中顶点的数量。如果 $V_x$ 和 $V_y$ 之间存在一条边,则 $A[V_x][V_y]=1$ 且 $A[V_y][V_x]=1$,否则值为零。对于有向图,如果 $V_x$ 和 $V_y$ 之间存在一条边,则 $A[V_x][V_y]=1$,否则值为零。
无向图的邻接矩阵
让我们考虑以下无向图并构造其邻接矩阵:
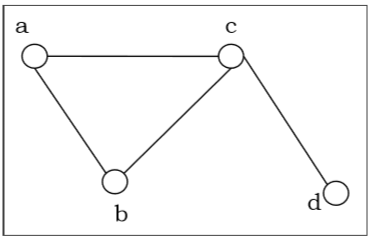
上述无向图的邻接矩阵将是:
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
1 |
0 |
1 |
0 |
c |
1 |
1 |
0 |
1 |
d |
0 |
0 |
1 |
0 |
有向图的邻接矩阵
让我们考虑以下有向图并构造其邻接矩阵:
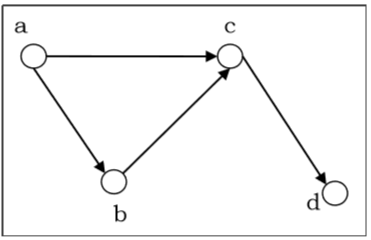
上述有向图的邻接矩阵将是:
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
0 |
b |
0 |
0 |
1 |
0 |
c |
0 |
0 |
0 |
1 |
d |
0 |
0 |
0 |
0 |
邻接表
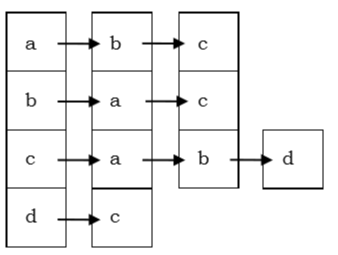
在邻接表中,一个链接列表数组 $(A[V])$ 用于表示具有 V 个顶点的图 G。条目 $A[V_x]$ 表示与第 Vx 个顶点相邻的顶点的链接列表。无向图的邻接表如下图所示:
平面图与非平面图
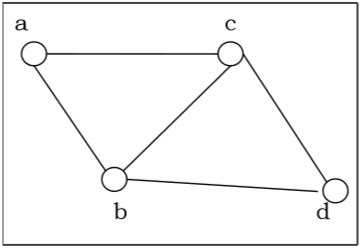
平面图 − 如果图 $G$ 可以绘制在平面上而不出现任何边交叉,则称其为平面图。如果我们在平面上绘制图而不出现边交叉,则称为将图嵌入平面。
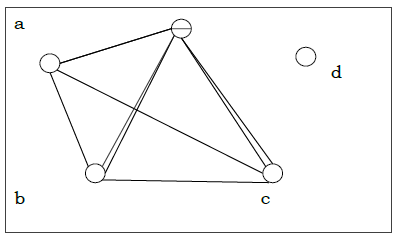
非平面图 − 如果图不能在平面上绘制而没有图边交叉,则该图是非平面图。
同构
如果两个图 G 和 H 包含相同数量的以相同方式连接的顶点,则它们称为同构图(用 $G \cong H$ 表示)。
检查非同构比检查同构更容易。如果出现以下任何条件,则两个图是非同构的:
- 连通分量的数量不同
- 顶点集基数不同
- 边集基数不同
- 度数序列不同
示例
以下图是同构的:
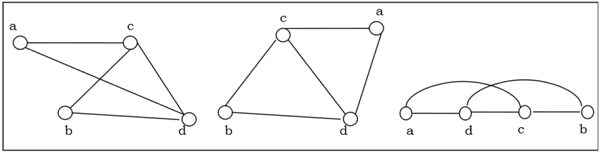
同态
从图 $G$ 到图 $H$ 的同态是一个映射(可能不是双射映射)$h: G \rightarrow H$,使得 − $(x, y) \in E(G) \rightarrow (h(x), h(y)) \in E(H)$。它将图 $G$ 的相邻顶点映射到图 $H$ 的相邻顶点。
同态的性质
如果同态是双射映射,则它是同构。
同态总是保持图的边和连通性。
同态的组合也是同态。
确定是否存在另一个图的任何同态图是一个 NP 完全问题。
欧拉图
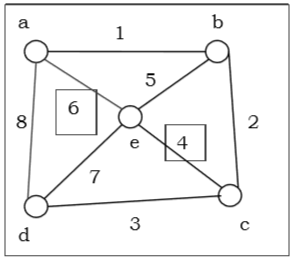
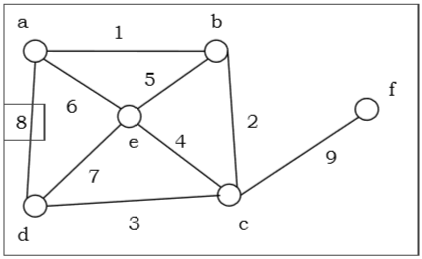
如果存在一个包含图 G 的每条边的闭合轨迹,则连通图 $G$ 称为欧拉图。欧拉路径是一条恰好使用图的每条边一次的路径。欧拉路径的起点和终点不同。
欧拉回路是一个恰好使用图的每条边一次的回路。欧拉回路总是从同一个顶点开始和结束。连通图 $G$ 是欧拉图当且仅当 $G$ 的所有顶点都是偶数度,并且连通图 $G$ 是欧拉图当且仅当它的边集可以分解成环。
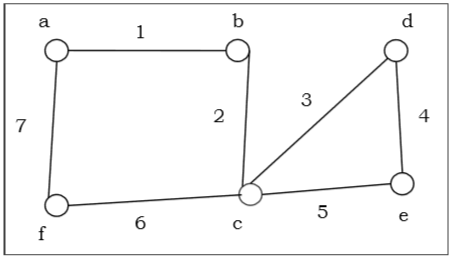
上图是一个欧拉图,因为“a 1 b 2 c 3 d 4 e 5 c 6 f 7 g”包含了图的所有边。
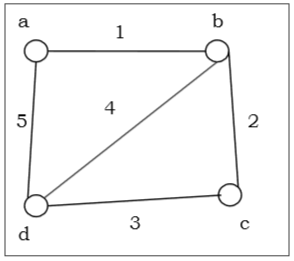
哈密顿图
如果存在一个包含 G 的每个顶点的环,则连通图 $G$ 称为哈密顿图,并且该环称为哈密顿环。图 G 中的哈密顿行走是一条恰好经过每个顶点一次的行走。
如果 G 是一个具有 n 个顶点的简单图,其中 $n \geq 3$,如果对于每个顶点 v,$deg(v) \geq \frac{n}{2}$,则图 G 是哈密顿图。这称为狄拉克定理。
如果 G 是一个具有 n 个顶点的简单图,其中 $n \geq 2$,如果对于每对不相邻的顶点 x 和 y,$deg(x) + deg(y) \geq n$,则图 G 是哈密顿图。这称为奥尔定理。