
微分器和积分器
执行微分和积分等数学运算的电子电路分别称为微分器和积分器。
本章详细讨论了基于运放的微分器和积分器。请注意,这些也属于运放的线性应用。
微分器
微分器是一种电子电路,其输出等于其输入的一阶导数。本节详细讨论了基于运放的微分器。
基于运放的微分器产生一个输出,该输出等于施加到其反相输入端的输入电压的微分。基于运放的微分器的电路图如下所示:
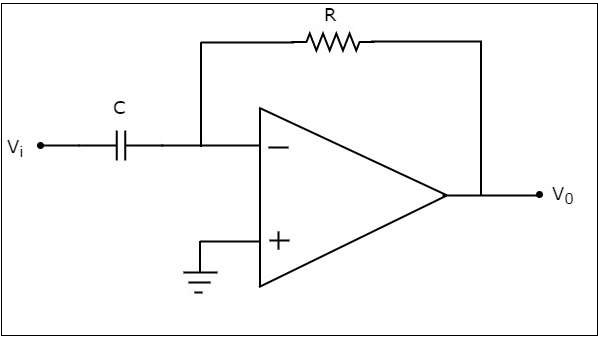
在上图电路中,运放的反相输入端连接到地。这意味着零伏特施加到其反相输入端。
根据虚短概念,运放反相输入端的电压将等于其同相输入端的电压。因此,运放反相输入端的电压将为零伏特。
反相输入端节点的节点方程为:
$$C\frac{\text{d}(0-V_{i})}{\text{d}t}+\frac{0-V_0}{R}=0$$
$$=>-C\frac{\text{d}V_{i}}{\text{d}t}=\frac{V_0}{R}$$
$$=>V_{0}=-RC\frac{\text{d}V_{i}}{\text{d}t}$$
如果$RC=1\sec$,则输出电压$V_{0}$将为:
$$V_{0}=-\frac{\text{d}V_{i}}{\text{d}t}$$
因此,上面所示的基于运放的微分器电路将产生一个输出,该输出是输入电压$V_{i}$的微分,当电阻和电容的阻抗大小互为倒数时。
请注意,输出电压$V_{0}$带有负号,这表示输入和输出之间存在1800的相位差。
积分器
积分器是一种电子电路,其输出是施加输入的积分。本节讨论了基于运放的积分器。
基于运放的积分器产生一个输出,该输出是施加到其反相输入端的输入电压的积分。基于运放的积分器的电路图如下所示:
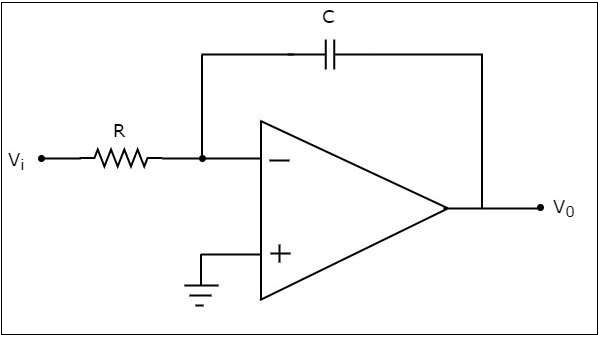
在上图所示的电路中,运放的同相输入端连接到地。这意味着零伏特施加到其同相输入端。
根据虚短概念,运放反相输入端的电压将等于其同相输入端的电压。因此,运放反相输入端的电压将为零伏特。
反相输入端的节点方程为:
$$\frac{0-V_i}{R}+C\frac{\text{d}(0-V_{0})}{\text{d}t}=0$$
$$=>\frac{-V_i}{R}=C\frac{\text{d}V_{0}}{\text{d}t}$$
$$=>\frac{\text{d}V_{0}}{\text{d}t}=-\frac{V_i}{RC}$$
$$=>{d}V_{0}=\left(-\frac{V_i}{RC}\right){\text{d}t}$$
对上述方程两边积分,得到:
$$\int{d}V_{0}=\int\left(-\frac{V_i}{RC}\right){\text{d}t}$$
$$=>V_{0}=-\frac{1}{RC}\int V_{t}{\text{d}t}$$
如果$RC=1\sec$,则输出电压$V_{0}$将为:
$$V_{0}=-\int V_{i}{\text{d}t}$$
因此,上面讨论的基于运放的积分器电路将产生一个输出,该输出是输入电压$V_{i}$的积分,当电阻和电容的阻抗大小互为倒数时。
注意 - 输出电压$V_{0}$带有负号,这表示输入和输出之间存在1800的相位差。