整流器
交流电（AC）和直流电（DC）是你在学习电荷流动时经常遇到的两个术语。交流电（AC）具有持续改变其状态的特性。例如，如果我们考虑正弦波，电流在正半周内沿一个方向流动，在负半周内沿相反方向流动。另一方面，直流电（DC）只沿一个方向流动。
当向电子电路输入交流电信号时，如果该电路产生直流信号或脉冲直流信号，则该电路称为整流器。本章将详细讨论基于运算放大器的整流器。
整流器的类型
整流器分为两种类型：半波整流器和全波整流器。本节将详细讨论这两种类型。
半波整流器
半波整流器是一种整流器，它在输入的一个半周期内在输出端产生正半周期，而在输入的另一个半周期内输出为零。
半波整流器的电路图如下所示。
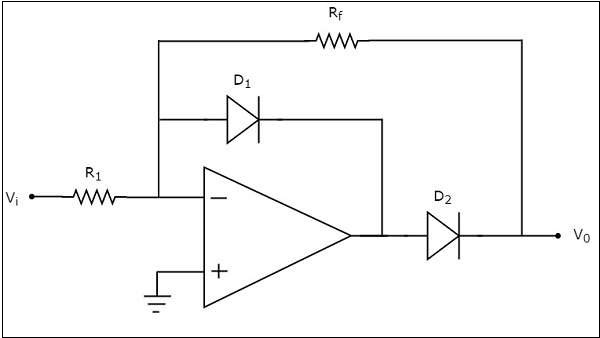
观察到上面所示的半波整流器电路图看起来像一个反相放大器，此外还有两个二极管D1和D2。
下面解释了上面所示的半波整流器电路的工作原理
对于正弦输入的正半周期，运算放大器的输出将为负。因此，二极管D1将被正向偏置。
当二极管D1正向偏置时，运算放大器的输出电压将为-0.7 V。因此，二极管D2将被反向偏置。因此，上述电路的输出电压为零伏。
因此，对于正弦输入的正半周期，半波整流器没有（零）输出。
对于正弦输入的负半周期，运算放大器的输出将为正。因此，二极管D1和D2将分别被反向偏置和正向偏置。因此，上述电路的输出电压将为−
V0=−(RfR1)V1
因此，对于正弦输入的负半周期，半波整流器的输出将为正半周期。
波形
半波整流器的输入和输出波形如下所示。
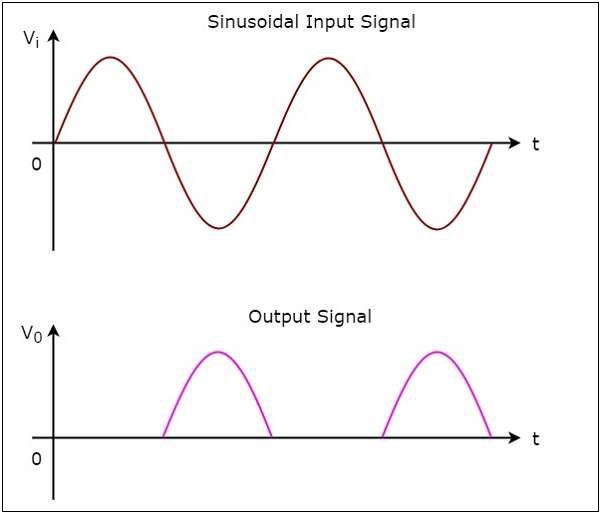
从上图可以看出，我们讨论的半波整流器电路图将为正弦输入的负半周期产生正半周期，并为正弦输入的正半周期产生零输出。
全波整流器
全波整流器在输入的两个半周期内都在输出端产生正半周期。
电路图如下所示：
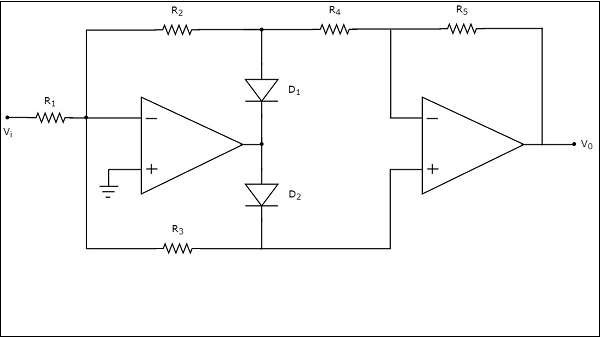
上述电路图包括两个运算放大器、两个二极管D1和D2以及五个电阻R1到R5。下面解释了上面所示的全波整流器电路的工作原理：
对于正弦输入的正半周期，第一个运算放大器的输出将为负。因此，二极管D1和D2将分别被正向偏置和反向偏置。
然后，第一个运算放大器的输出电压将为−
V01=−(R2R1)Vi
观察到第一个运算放大器的输出连接到电阻R4，该电阻连接到第二个运算放大器的反相输入端。第二个运算放大器的同相输入端的电压为0 V。因此，第二个运算放大器与电阻R4和R5一起充当反相放大器。
第二个运算放大器的输出电压将为
V0=−(R5R4)V01
代入上述公式中的V01值，得到−
=>V0=−(R5R4){−(R2R1)Vi}
=>V0=(R2R5R1R4)Vi
因此，对于正弦输入的正半周期，全波整流器的输出将为正半周期。在这种情况下，输出的增益为R2R5R1R4。如果我们考虑R1=R2=R4=R5=R，则输出的增益将为1。
对于正弦输入的负半周期，第一个运算放大器的输出将为正。因此，二极管D1和D2将分别被反向偏置和正向偏置。
第一个运算放大器的输出电压将为−
V01=−(R3R1)Vi
第一个运算放大器的输出直接连接到第二个运算放大器的同相输入端。现在，第二个运算放大器与电阻R4和R5一起充当同相放大器。
第二个运算放大器的输出电压将为−
V0=(1+R5R4)V01
代入上述公式中的V01值，得到
=>V0=(1+R5R4){−(R3R1)Vi}
=>V0=−(R3R1)(1+R5R4)Vi
因此，对于正弦输入的负半周期，全波整流器的输出也将为正半周期。在这种情况下，输出增益的大小为(R3R1)(1+R5R4)。如果我们考虑R1=2R3=R4=R5=R，则输出的增益将为1。
全波整流器的输入和输出波形如下所示。
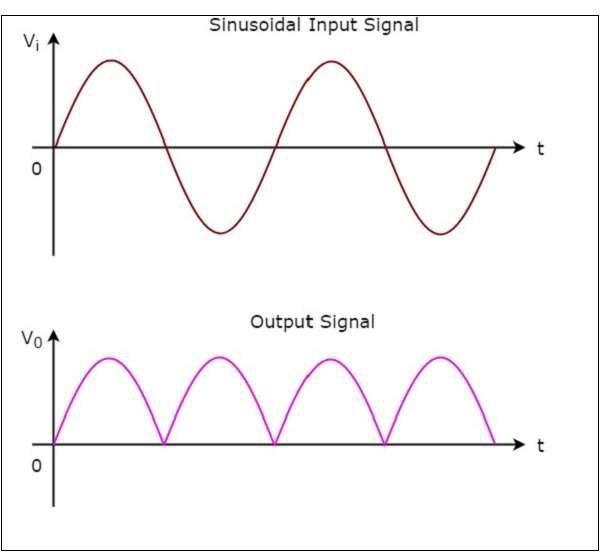
从上图可以看出，我们考虑的全波整流器电路图将仅为正弦输入的正半周期和负半周期产生正半周期。