正弦波振荡器

---

---

振荡器是一种产生周期性信号的电子电路。如果振荡器产生正弦波振荡，则称为正弦波振荡器。它将来自直流电源的输入能量转换为具有周期性信号的交流输出能量。此周期性信号将具有特定的频率和幅度。

正弦波振荡器的框图如下所示：

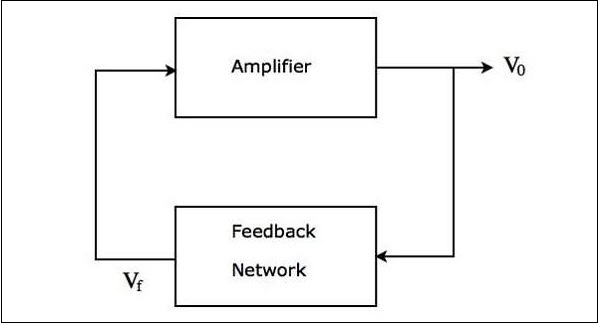
上图主要由两个模块组成：放大器和反馈网络。反馈网络将放大器输出的一部分作为输入，并产生电压信号。此电压信号用作放大器的输入。

当满足以下两个条件时，上图所示的正弦波振荡器框图产生正弦波振荡：

• 上述正弦波振荡器框图的环路增益$A_{v}\beta$必须大于或等于1。这里，$A_{v}$和$\beta$分别为放大器的增益和反馈网络的增益。

• 上述正弦波振荡器框图环路的总相移必须为0⁰或360⁰。

上述两个条件合称为巴克豪森判据。

基于运放的振荡器

有两种类型的基于运放的振荡器。

• RC移相振荡器
• 维恩电桥振荡器

本节将详细讨论每个振荡器。

RC移相振荡器

基于运放的振荡器，它借助反相放大器和反馈网络在输出端产生正弦电压信号，被称为RC移相振荡器。此反馈网络由三个级联的RC网络组成。

RC移相振荡器的电路图如下所示：

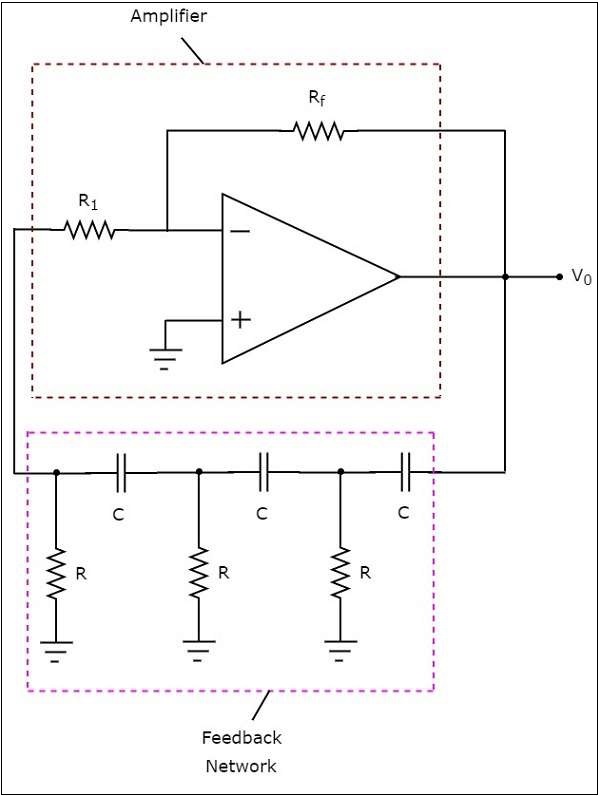
在上图电路中，运放工作在反相模式。因此，它提供180⁰的相移。上述电路中存在的反馈网络也提供180⁰的相移，因为每个RC网络提供60⁰的相移。因此，上述电路在某个频率下提供360⁰的总相移。

• RC移相振荡器的输出频率为：

$$f=\frac{1}{2\Pi RC\sqrt[]{6}}$$

• 反相放大器的增益$A_{v}$应大于或等于-29，

$$即，-\frac{R_f}{R_1}\geq-29$$

$$=>\frac{R_f}{R_1}\geq-29$$

$$=>R_{f}\geq29R_{1}$$

因此，为了在RC移相振荡器的输出端产生持续振荡，我们应将反馈电阻$R_{f}$的值至少考虑为电阻$R_{1}$值的29倍。

维恩电桥振荡器

基于运放的振荡器，它借助同相放大器和反馈网络在输出端产生正弦电压信号，被称为维恩电桥振荡器。

维恩电桥振荡器的电路图如下所示：

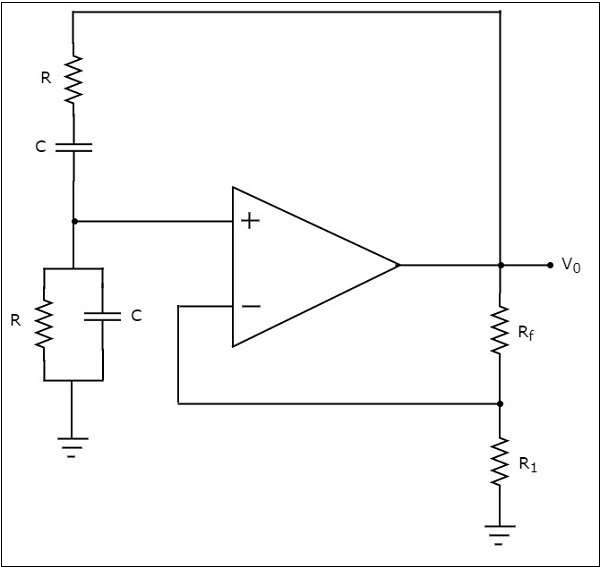
在上述维恩电桥振荡器电路中，运放工作在同相模式。因此，它提供00的相移。所以，上述电路中存在的反馈网络不应提供任何相移。

如果反馈网络提供了一些相移，则我们必须平衡电桥，以使不存在任何相移。因此，上述电路在某个频率下提供0⁰的总相移。

• 维恩电桥振荡器的输出频率为

$$f=\frac{1}{2\Pi RC}$$

• 同相放大器的增益$A_{v}$应大于或等于3

$$即，1+\frac{R_f}{R_1}\geq3$$

$$=>\frac{R_f}{R_1}\geq2$$

$$=>R_{f}\geq2R_{1}$$

因此，为了在维恩电桥振荡器的输出端产生持续振荡，我们应将反馈电阻$R_{f}$的值至少考虑为电阻$R_{1}$值的2倍。