数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究阿基拉去她村里的一个集市。她想玩旋转木马和套圈游戏（一种你用圈套住摊位上物品的游戏，如果圈完全覆盖了任何物品，你就可以得到它）。她玩套圈游戏的次数是她乘坐旋转木马次数的一半。每次乘坐旋转木马要花费3卢比，玩一次套圈游戏要花费4卢比。如果她在集市上花了20卢比，请用代数和图形表示这种情况。
已知
阿基拉玩套圈游戏的次数是她乘坐旋转木马次数的一半。
每次乘坐的费用 = 3 卢比
玩一次套圈游戏的费用 = 4 卢比。
在集市上花费的总金额 = 20 卢比。
要求
我们需要用代数和图形表示上述情况。
解答
设 $x$ 为阿基拉乘坐旋转木马的次数，$y$ 为她玩套圈游戏的次数。
根据题意，
$y = \frac{1}{2}x$
$\Rightarrow x-2y = 0$.....(i)
$3x + 4y = 20$......(ii)
$4y=20-3x$
$y=\frac{20-3x}{4}$
为了用图形表示上述方程，我们需要每个方程至少两个解。
对于方程 (i)，
如果 $x=0$，则 $y=\frac{0}{2}=0$
如果 $x=2$，则 $y=\frac{2}{2}=1$
| $x$ | 0 | 2 |
| $y=\frac{1}{2}x$ | 0 | 1 |
对于方程 (ii)，
如果 $x=0$，则 $y=\frac{20-3(0)}{4}=5$
如果 $y=0$，则 $0=\frac{20-3x}{4}$
$\Rightarrow 20=3x$
$\Rightarrow x=\frac{20}{3}$，这不是整数，因此不容易在坐标纸上绘制。
所以，让我们取 $y=2$
如果 $y=2$，则 $2=\frac{20-3x}{4}$
$\Rightarrow 20-3x=8$
$\Rightarrow 3x=20-8$
$\Rightarrow x=\frac{12}{3}$
$\Rightarrow x=4$
| $x$ | 0 | $\frac{20}{3}$ | 4 |
$y=\frac{20-3x}{4}$ | 5 | 0 | 2 |
上述情况可以用图形表示如下
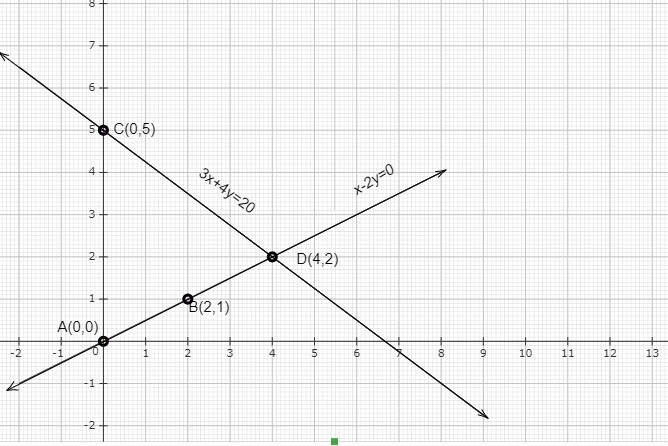
直线 AB 表示方程 $x-2y=0$，直线 CD 表示方程 $3x+4y=20$。
两条直线在 D(4,2) 点相交，这是两个方程的解。
278 次浏览
