求一个四边形的面积，已知其对角线的长度为26厘米，从对角线的两端到另一对顶点的垂线的长度分别为11.2厘米和12.8厘米。

已知

一个四边形的对角线长为26厘米，从对角线的两端到另一对顶点的垂线的长度分别为11.2厘米和12.8厘米。

求解

我们需要求出这个四边形的面积。

解答

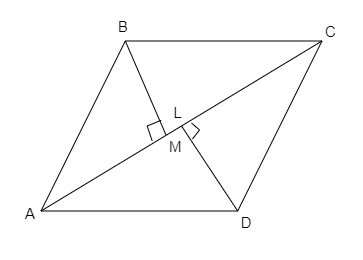
$AC=26\ cm, DL=12.8\ cm, BM=11.2\ cm$

三角形ACD的面积$= \frac{1}{2}\times AC\times DL$

$= \frac{1}{2}\times 26\times 12.8$

$=166.4\ cm^2$ 

三角形ABC的面积$= \frac{1}{2}\times AC\times BM$

$= \frac{1}{2}\times 26\times 11.2$

$=145.6\ cm^2$ 

因此，

四边形的面积$=三角形ACD的面积+三角形ABC的面积$

$=(166.4+145.6)\ cm^2$

$=312\ cm^2$

四边形的面积为$312\ cm^2$。

教程点

更新于: 2022年10月10日

393 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习