从半径为$3 \mathrm{~cm}$的圆形硬纸板上剪掉两个$90^{\circ}$的扇形。求剩余部分的周长，精确到百分之一厘米（取$\pi=22 / 7)$

已知

从半径为$3 \mathrm{~cm}$的圆形硬纸板上剪掉两个$90^{\circ}$的扇形。

要求

我们需要求剩余部分的周长，精确到百分之一厘米。

解答

如图所示，设硬纸板为$ABCD$。

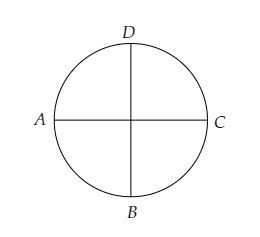
剪掉了两个$90^{\circ}$的扇形。

这意味着，

我们得到一个半圆形的硬纸板。

设$ABD$为剩余的硬纸板。

因此，

弧$ABD$的周长=$\frac{1}{2}(2 \pi r)$

$=\pi (3)$

$=\frac{22}{7} \times 3$

$=\frac{66}{7}$

$=9.428 \mathrm{~cm}$

剩余部分的周长，精确到百分之一厘米，是 $9.428 \mathrm{~cm}$。

教程点

更新时间： 2022年10月10日

123 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习