如果A、B和C是直线上的三个点，且AC=8cm，CB=4cm，AB=12cm，那么哪一点A、B或C位于其他两点之间？
已知：
如果A、B和C是直线上的三个点，且AC =8cm，CB=4cm，AB=12cm
求解：找出哪一点A、B或C位于其他两点之间
解答
A、B、C在一条直线上
$AB = 12$ cm
$CB = 4$ cm
$AC = 8$ cm
$ AC + CB = 8 + 4$
= 12 CM
$AC + CB = AB$
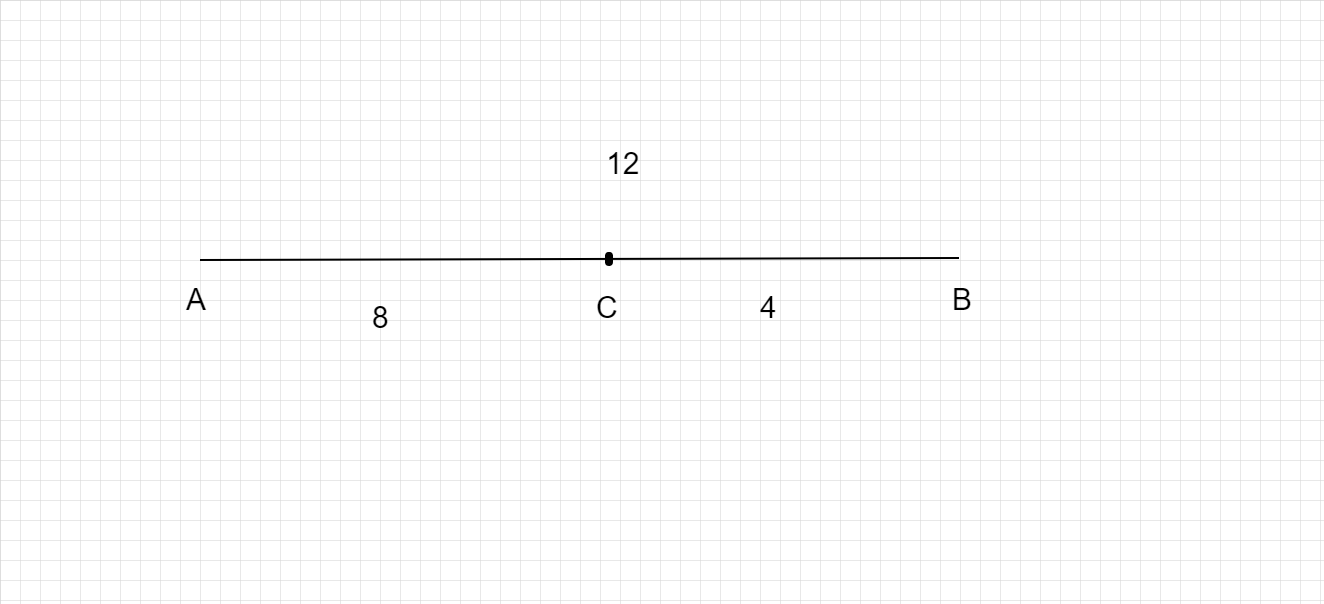
所以，C位于A和B之间
- 相关文章
- 如果A、B、C是直线上的三个点，且AB = 5 cm，BC = 3 cm，AC = 8 cm，那么哪一个位于其他两个之间？
- 如果\( \mathrm{A}, \mathrm{B}, \mathrm{C} \)是直线上的三个点，且\( \mathrm{AB}=5 \mathrm{~cm}, \mathrm{BC}=3 \mathrm{~cm} \)和\( \mathrm{AC}=8 \mathrm{~cm} \)，哪一个位于其他两个之间？
- 如果点\( C \)位于两点\( A \)和\( B \)之间，使得\( AC=BC \)，则证明\( \mathrm{AC}=\frac{1}{2} \mathrm{AB} \)。通过绘制图形进行解释。
- 画任意一条线段，例如\( \overline{\mathrm{AB}} \)。取任意一点\( \mathrm{C} \)位于\( \mathrm{A} \)和\( \mathrm{B} \)之间。测量\( AB, BC \)和\( AC \)的长度。是否\( AB=AC+CB \)？[注意：如果\( A, B, C \)是直线上的任意三点，使得\( AC+CB=AB \)，那么我们可以确定\( \mathrm{C} \)位于\( \mathrm{A} \)和\( \mathrm{B} \)之间。]
- 在给定图形中，$A, B$和$C$分别是$OP, OQ$和$OR$上的点，使得$AB \| PQ$和$AC \| PR$。证明$BC \| QR$。
- 画一条线段，比如AB。取任意一点C位于A和B之间。测量AB，BC和AC的长度。是否$AB = AC + CB $？
- 如果点A和B的坐标分别为$( -2,\ -2)$和$( 2,\ -4)$，求P的坐标，使得\ $AP=\frac{3}{7} AB$，其中P位于线段AB上。
- 如果$A$和$B$分别为$(-2, -2)$和$(2, -4)$，求$P$的坐标，使得$AP = \frac{3}{7}AB$且$P$位于线段$AB$上。
- $AB$是一条线段，$P$和$Q$是$AB$两侧的点，使得它们都与点$A$和$B$等距。证明直线$PQ$是$AB$的垂直平分线。
- 画任意一条线段，比如AB。取任意一点C位于A和B之间。测量AB，BC和AC的长度。是否AB =AC+CB？
- 过点A、B、C两两作直线，并标记三个不共线的点A、B、C。
- 证明点$P( a,\ b+c),\ Q( b,\ c+a)$和$R( c,\ a+b)$共线。
- 作一个$\vartriangle ABC$，使得$AB=6$，$AC=5\ cm$，底边$B C$为$4\ cm$。
- 画任意一条线段，比如$\overline{AB}$。取任意一点C位于两者之间。测量AB，BC和AC的长度。是否$AB=AC+CB$？
- 如果a和b是两个奇正整数，且a $>$ b，则证明两个数$\frac{a\ +\ b}{2}$和$\frac{a\ -\ b}{2}$中有一个是奇数，另一个是偶数。
数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究