数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究如果点 A(1, -2), B(2, 3), C(a, 2) 和 D(-4, -3) 构成一个平行四边形，求 a 的值和平行四边形以 AB 为底的高。
已知
点 A(1, -2), B(2, 3), C(a, 2) 和 D(-4, -3) 构成一个平行四边形。
要求
我们必须找到 a 的值和平行四边形以 AB 为底的高。
解答
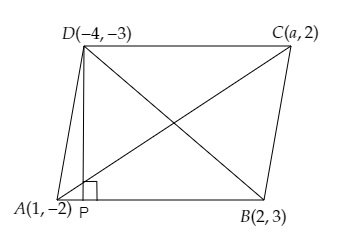
从 D 点向 AB 作垂线，垂足为 P。
DP 是平行四边形的高。
我们知道：
平行四边形的对角线互相平分。
这意味着：
AC 的中点 = BD 的中点
连接点 (x₁, y₁) 和 (x₂, y₂) 的线段的中点是 ((x₁+x₂)/2, (y₁+y₂)/2)
((1+a)/2, (-2+2)/2) = ((2-4)/2, (3-3)/2)
比较后，我们得到：
=> (1+a)/2 = -2/2 = -1
=> 1+a = -2
=> a = -3
a 的值为 -3。
我们知道：
对角线将三角形分成两个面积相等的三角形。
这意味着：
平行四边形 ABCD 的面积 = 三角形 ABC 的面积 + 三角形 ADC 的面积。
= 2 × 三角形 ABC 的面积
我们知道：
顶点为 (x₁,y₁), (x₂,y₂), (x₃,y₃) 的三角形的面积由下式给出：
三角形面积 = 1/2[x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)]
因此：
三角形 ABC 的面积 = 1/2[1(3-2) + 2(2+2) + (-3)(-2-3)]
= 1/2[1(1) + 2(4) + (-3)(-5)]
= 1/2[1 + 8 + 15]
= 1/2 × 24
= 12 平方单位。
因此：
平行四边形 ABCD 的面积 = 2 × 12 = 24 平方单位。
平行四边形的面积 = 底 × 高
高 = 面积 ÷ 底
DP = 24/AB
根据距离公式，我们得到：
AB = √[(2-1)² + (3+2)²]
= √(1² + 5²)
= √(1 + 25)
= √26
因此：
DP = 24/√26
= (24√26) / (√26√26)
= (24√26) / 26
= (12√26) / 13
以 AB 为底的平行四边形的高是 (12√26)/13。
49 次查看
