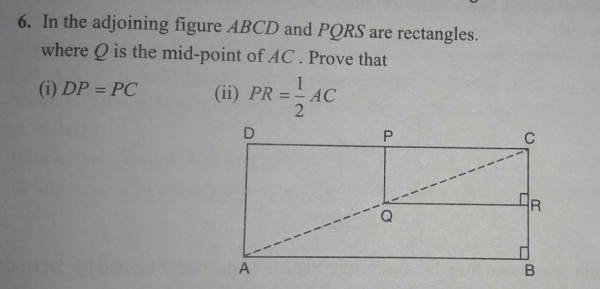
下图中...
 "\n
"\n
解决方案
给定 ABCD 和 PQRS 为矩形。
AC 为对角线,Q 为 AC 的中点。
因此 AQ = QC
(i)
AD || PQ 在三角形 ACD 中。
根据基本比例定理
DP/PC = AQ/QC = 1/1
因此 DP = PC
(ii)
我们知道 AQ = QC = 1/2 AC
在矩形 PQRS 中,对角线 PR 和 QC 等长且相互平分。
因此 PR = QC = 1/2 AC 或
PR = 1/2 AC

广告
 "\n
"\n解决方案
给定 ABCD 和 PQRS 为矩形。
AC 为对角线,Q 为 AC 的中点。
因此 AQ = QC
(i)
AD || PQ 在三角形 ACD 中。
根据基本比例定理
DP/PC = AQ/QC = 1/1
因此 DP = PC
(ii)
我们知道 AQ = QC = 1/2 AC
在矩形 PQRS 中,对角线 PR 和 QC 等长且相互平分。
因此 PR = QC = 1/2 AC 或
PR = 1/2 AC
