在下列图形中求出∠A。
 "\n
"\n
已知条件
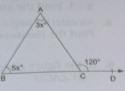
$\angle BAC=3x^o$, $\angle ABC=5x^o$,且 $\angle ACD=120^o$。
求解
我们要求出∠A 的度数。
解法
我们知道:
三角形每条外角的度数等于其对角和非邻角内角的度数之和。
因此,
$3x^o+5x^o=120^o$
$8x^o=120^o$
$x=\frac{120^o}{8}$
$x=15^o$
$3x^o=3(15^o)=45^o$
∠A 的度数为 $45^o$。

广告
 "\n
"\n已知条件
$\angle BAC=3x^o$, $\angle ABC=5x^o$,且 $\angle ACD=120^o$。
求解
我们要求出∠A 的度数。
解法
我们知道:
三角形每条外角的度数等于其对角和非邻角内角的度数之和。
因此,
$3x^o+5x^o=120^o$
$8x^o=120^o$
$x=\frac{120^o}{8}$
$x=15^o$
$3x^o=3(15^o)=45^o$
∠A 的度数为 $45^o$。
