在下面的图形中,$\angle B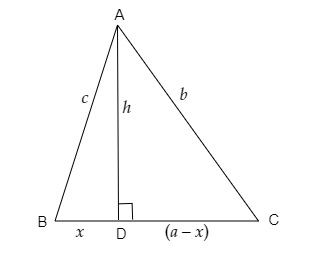 "\n
"\n
已知
$\angle B<90^o$,线段 $AD \perp BC$。
求解
需要证明 $b^2=h^2+a^2+x^2-2ax$。
解法
在 $\triangle ADC$ 中,根据勾股定理,
$ AC^2=AD^2+DC^2$
$b^2=h^2+(a-x)^2$
$b^2=h^2+a^2+x^2-2ax$
因此,证毕。

广告
 "\n
"\n已知
$\angle B<90^o$,线段 $AD \perp BC$。
求解
需要证明 $b^2=h^2+a^2+x^2-2ax$。
解法
在 $\triangle ADC$ 中,根据勾股定理,
$ AC^2=AD^2+DC^2$
$b^2=h^2+(a-x)^2$
$b^2=h^2+a^2+x^2-2ax$
因此,证毕。
