证明在平行四边形中：
1）对边相等
2）对角相等
3）每条对角线将平行四边形分成两个全等三角形

已知

我们必须证明，在平行四边形中：

1）对边相等

2）对角相等

3）每条对角线将平行四边形分成两个全等三角形

解

取平行四边形 ABCD，连接

其不相邻的两个顶点，例如 A 和 C。

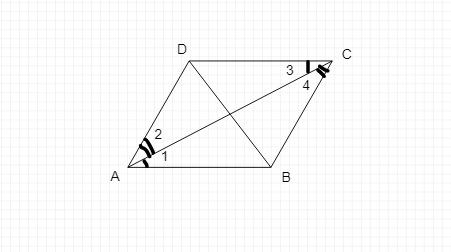
在平行四边形 ABCD 中，

BC || AD 且 AB || DC。

AC 是平行线 BC 和 AD 的截线，也是平行线 AB 和 DC 的截线。

设由这些平行线和截线形成的角为 1、2、3 和 4。

考虑△ABC 和△CDA，

∠1 = ∠3 (因为内错角相等)

∠2 = ∠4 (因为内错角相等)

AC = CA (公共边)

因此，根据 ASA 定理，△ABC ≅ △CDA。

因此，对角线 AC 将

平行四边形 ABCD 分成两个全等三角形 ABC 和 CDA.

在全等三角形 ABC 和 CDA 中，

BC = DA (全等三角形的对应边)

同样，BA = DC。

BC 和 DA；BA 和 DC 是平行四边形 ABCD 中的对边。

因此，在平行四边形中，对边相等。

Tutorialspoint

更新于：2022年10月10日

72 次浏览

开启你的职业生涯

完成课程，获得认证

开始学习