证明平行四边形的对角线将其分成四个面积相等的三角形。

待办事项

我们需要证明平行四边形的对角线将其分成四个面积相等的三角形。
 解答

设在平行四边形 $ABCD$ 中，对角线 $AC$ 和 $BD$ 相交于 $O$。

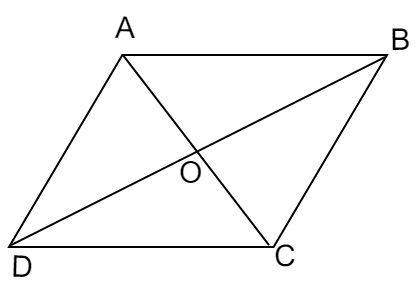
我们知道，

平行四边形的对角线互相平分。

这意味着，

$OA = OC$ 且 $OB = OD$。

三角形的中线将其分成两个面积相等的三角形。

在 $\triangle ABC$ 中，$BO$ 是中线。

这意味着，

$ar (\triangle OAB) = ar (\triangle OBC)$.........(i)

在 $\triangle ABD$ 中，$AO$ 是中线。

这意味着，

$ar (\triangle OAB) = ar (\triangle OAD)$.......(ii)

在 $\triangle ACD$ 中，$DO$ 是中线。

这意味着，

$ar (\triangle OAD) = ar (\triangle OCD)$.........(iii)

由 (i)、(ii) 和 (iii)，我们得到，

$ar (\triangle OAB) = ar (\triangle OBC) = ar (\triangle OCD) = ar(\triangle OAD)$

证毕。

教程点

更新于: 2022年10月10日

112 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习