数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学证明平行四边形的对角线将其分成两个全等三角形。
已知
平行四边形的对角线将其分成两个全等三角形。
需要证明
我们需要证明平行四边形的对角线将其分成两个全等三角形。
解答
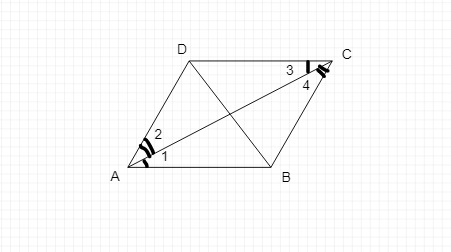
取平行四边形ABCD，连接其任意两个不相邻的顶点，例如A和C。
在平行四边形ABCD中，BC平行于AD，AB平行于DC。
AC是平行线BC和AD的截线，也是平行线AB和DC的截线。
设由这些平行线和截线形成的角为角1、2、3和4。
考虑△ABC和△CDA，
∠1 = ∠3 (因为内错角相等)
∠2 = ∠4 (因为内错角相等)
AC = CA (公共边)
因此，根据ASA定理，△ABC ≅ △CDA。
因此，对角线AC将平行四边形ABCD分成两个全等三角形ABC和CDA。
证毕。
更新于：2022年10月10日
828 次浏览
广告