数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究你在九年级学过，三角形的中线将其分成两个面积相等的三角形。验证一下顶点为 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$ 的 $∆ABC$ 的结果。
已知
三角形的顶点为 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$。
操作
我们需要证明三角形的中线将其分成两个面积相等的三角形。
解答
设 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$ 为三角形 $ABC$ 的顶点。
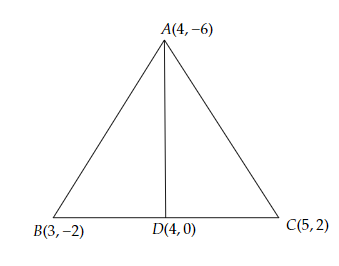
设 $D$ 为 $\triangle ABC$ 的边 $BC$ 的中点。
这意味着，
点 $D$ 的坐标 = BC 的中点 $= (\frac{3+5}{2}, \frac{-2+2}{2})$
$=(\frac{8}{2}, 0)$
$=(4, 0)$
$AD$ 是 $\triangle ABC$ 的中线。
$\triangle \mathrm{ABD}$ 的面积 $=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$
$=\frac{1}{2}[4 \times(-2-0)+3(0+6)+4(-6+2)]$
$=\frac{1}{2}[-8+18-16]$
$=\frac{-6}{2}$
$=3$ 平方单位
$\triangle \mathrm{ADC}$ 的面积 $=\frac{1}{2}[4(0-2)+4(2+6)+5\times(-6-0)]$
$=\frac{1}{2}[-8+32-30]$
$=\frac{-6}{2}$
$=3$ 平方单位
$\triangle \mathrm{ABD}$ 的面积 = $\triangle \mathrm{ADC}$ 的面积
因此，三角形的中线将其分成两个面积相等的三角形。
证毕。
更新于: 2022 年 10 月 10 日
27 次浏览
广告