ABC 和 BDE 是两个等边三角形，D 是 BC 的中点。三角形 ABC 和 BDE 的面积之比是
(a) 2 :1
(b) 1:2
(c) 4:1
(d) 1:4

已知

ABC 和 BDE 是两个等边三角形，D 是 BC 的中点。

要求：

我们必须找到△ABC 和△BDE 的面积比。

解答

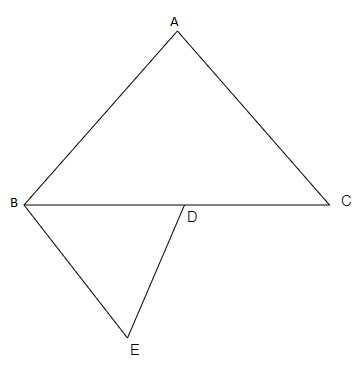
在△ABC 和△BDE 中，

∠A = ∠E (因为△ABC 和△BDE 是等边三角形)

∠ABC = ∠BED (因为△ABC 和△BDE 是等边三角形)

因此，

△ABC ∽ △BDE (AA相似)

我们知道，

如果两个三角形相似，则这两个三角形的面积之比与其对应边长的平方之比成正比。

因此，

ar(△ABC) / ar(△BDE) = BC² / BD²

= (2BD)² / BD² (D 是 BC 的中点)

= 4BD² / BD²

= 4/1

△ABC 和△BDE 的面积比是 4:1。

教程点

更新于：2022年10月10日

256 次浏览

开启你的职业生涯

完成课程获得认证

开始学习