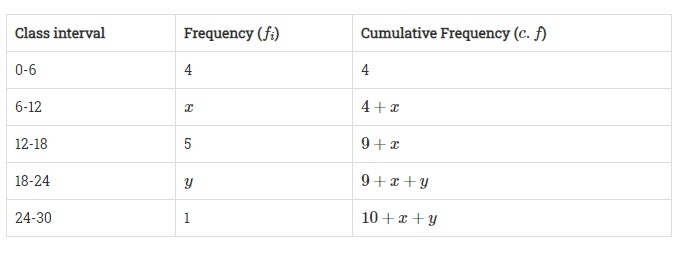
下面给出的分布的中位数是 14.4。如果总频数为 20，求 $x$ 和 $y$ 的值。

组距	0-6	6-12	12-18	18-24	24-30
频数	4	$x$	5	$y$	1

已知

给定分布的中位数为 14.4。总频数为 20。

要求

我们必须找到 $x$ 和 $y$ 的值。

解答

中位数 $= 14.4$ 且 $N = 20$

$10 + x + y = 20$

$x+y = 20 - 10 = 10$

$y = 10-x$.....….(i)

中位数 $= 14.4$，位于 12-18 组。

$l = 12, f= 5, F = 4+x$ 且 $h = 18-12=6$

中位数 $=l+(\frac{\frac{\mathrm{N}}{2}-\mathrm{F}}{f}) \times h$

$14.4=12+\frac{\frac{20}{2}-(4+x)}{5}\times 6$

$14.4-12=\frac{10-4-x}{5}\times6$

$2.4(5)=(6-x)6$

$12=36-6x$

$6x=36-12$

$x=\frac{24}{6}=4$

$y = 10 - 4 = 6$            [来自 (i)]

$x$ 和 $y$ 的值分别为 $4$ 和 $6$。 

教程点

更新于： 2022 年 10 月 10 日

168 次查看

开启你的 职业生涯

完成课程获得认证

开始学习