两根高分别为 6 米和 11 米的杆子垂直立于平地上。如果它们的底部相距 12 米，求它们顶端的距离。

已知

两根高分别为 6 米和 11 米的杆子垂直立于平地上。

它们的底部相距 12 米。

要求

我们要求出它们的顶端的距离。

解答

设 $DE$ 和 $AC$ 是分别高为 $6\ m$ 和 $11\ m$ 的两根杆子。

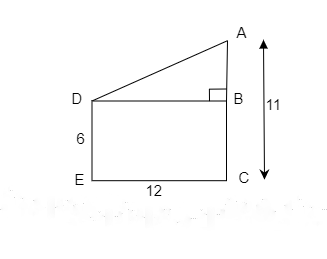
它们的底部距离 $EC= 12\ m$

这意味着，

$DB=12\ m$

在直角三角形 $ABD$ 中，

根据勾股定理，

$AB^2 + BD^2 = AD^2$

$5^2 + 12^2 = AD^2$   ($AB=AC-BC=11-6=5\ m$)

$AD^2 = 144 + 25$

$AD^2= 169$

$AD = \sqrt{169}=13$

因此，它们的顶端的距离为 $13\ m$。

教程点

更新于: 2022年10月10日

69 次浏览

开启你的职业生涯

完成课程获得认证

开始学习