什么是透镜的焦度？定义其SI单位。你分别有两个焦距为+10厘米和-10厘米的透镜A和B。说明每个透镜的性质和焦度。哪个透镜会形成一个物体放置在距透镜8厘米处的虚像和放大像？画一个光线图来证明你的答案。

透镜的焦度$P$定义为透镜汇聚或发散入射光束的能力。它也是其焦距的倒数。

也就是说，$P=\frac {1}{f}$

透镜焦度的SI单位是屈光度，用$D$表示。

已知

透镜A的焦距，$f_A=+10cm=+0.1m$ (已将厘米转换为米)

透镜B的焦距，$f_B=-10cm=-0.1m$ (已将厘米转换为米)

求解：每个透镜(A & B)的性质和焦度。

解答

计算透镜A的焦度。

我们知道透镜的焦度计算公式为：

$P=\frac {1}{f}$

将$f_A$的值代入上式，得到：

$P=\frac {1}{0.1}$

$P=\frac {10}{1}$

$P=+10D$

因此，透镜A的焦度为10D，正号表示其为会聚透镜或凸透镜。

现在，

计算透镜B的焦度。

我们知道透镜的焦度计算公式为：

$P=\frac {1}{f}$

将$f_B$的值代入上式，得到：

$P=\frac {1}{-0.1}$

$P=-\frac {10}{1}$

$P=-10D$

因此，透镜B的焦度为-10D，负号表示其为发散透镜或凹透镜。

对于凸透镜，当物体放置在焦点(F')内，或在光心(C)和焦点(F')之间时，所成的像总是虚像、正立和放大的。而凹透镜无论物体距离透镜多远，都产生虚像、正立但缩小的像。

这里，物体放置在距离透镜8厘米处，这个距离小于焦距。因此，在这种情况下，凸透镜会产生物体的虚像和放大像。

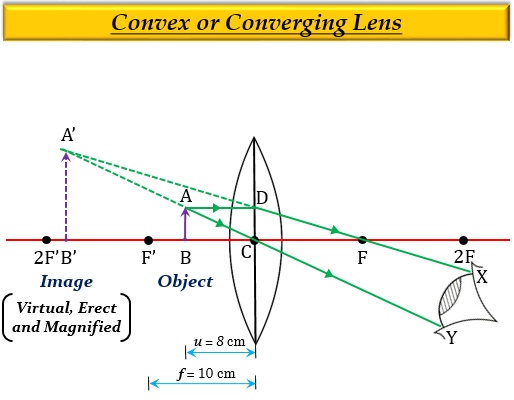
下图显示了这种情况：

教程点

更新于：2022年10月10日

300 次浏览

启动你的职业生涯

完成课程后获得认证

开始