象限

---

引言

笛卡尔平面是一个二维平面，它是坐标系的一部分。笛卡尔平面的概念主要用于欧几里得几何和代数。在二维平面系统中，任何点都可以由x坐标和y坐标指定。笛卡尔平面上的轴线将其划分为4个相等且无限的部分，称为象限。这些象限分别命名为第一象限、第二象限、第三象限和第四象限。在圆的情况下，象限可以用圆的四分之一来表示。因此，让我们简要研究笛卡尔平面和圆的象限主题。

笛卡尔平面

笛卡尔平面可以定义为由两个相互垂直的坐标轴相交形成的平面。水平轴是x轴，垂直轴称为y轴。x轴和y轴相交于一点，称为原点，用符号O表示。

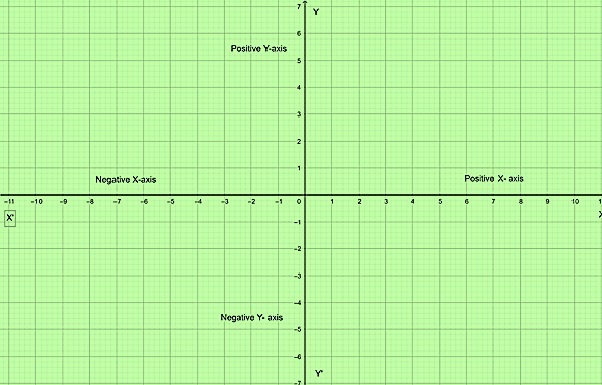
带有正负x轴和y轴的笛卡尔平面

笛卡尔平面的组成部分

笛卡尔平面具有三个主要组成部分：**轴、原点**和**象限**。当我们要在笛卡尔平面上定位任何点时，这些组成部分是必不可少的。笛卡尔平面的组成部分如下所示

轴

笛卡尔平面上的水平线和垂直线称为轴。水平轴称为x轴，垂直轴称为y轴。

原点

两条轴相交的点称为原点。它用O表示。原点的坐标为(0,0)。

象限

当x轴和y轴相互垂直时，它们将笛卡尔平面分成4个相等的部分。这些部分称为**象限**。

笛卡尔平面的象限

当x轴和y轴相互交叉时，它们将笛卡尔平面分成4个相等且无限的部分。这些部分称为象限。这些象限分别表示为第一象限、第二象限、第三象限和第四象限。

第一象限

第一象限位于笛卡尔平面的右上角。在这个象限中，x坐标和y坐标都是正数。

第二象限

第二象限位于笛卡尔平面的左上角。在这个象限中，x坐标为负数，y坐标为正数。

第三象限

第三象限位于笛卡尔平面的左下角。在这个象限中，x坐标和y坐标都是负数。

第四象限

第四象限位于笛卡尔平面的右下角。在这个象限中，x坐标为正数，y坐标为负数。

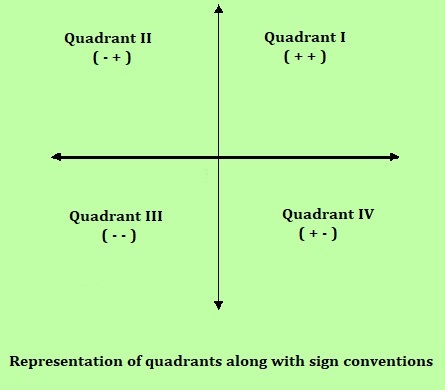
笛卡尔平面中象限的性质

• x轴的右侧被认为是正数，x轴的左侧被认为是负数。

• 类似地，上y轴被认为是正数，下y轴被认为是负数。

• 象限和负轴以及正轴在绘制图形中起着重要作用。

• x的值称为x坐标或横坐标。它表示该点到y轴的距离。

• 类似地，y的值称为y坐标或纵坐标。它表示该点到x轴的距离。

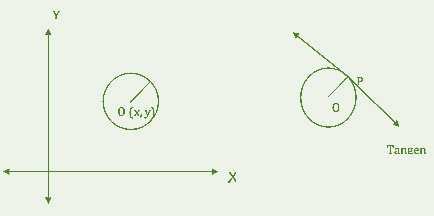
圆

在笛卡尔平面上，圆是在平面内运动的点的轨迹，保持与平面内给定固定点之间的距离恒定。

圆的象限

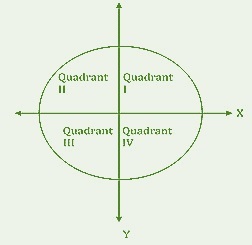
象限是笛卡尔系统中的四个四分之一。每个部分称为象限。在圆的情况下，圆的四分之一称为象限。圆的每个四分之一测量90⁰。这四个四分之一加起来共计360⁰。当我们连接这个象限时，我们会得到一个圆的形状。象限分别命名为第一象限、第二象限、第三象限和第四象限，如上图所示。

圆形象限的不同公式

• 象限面积 =$\mathrm{\frac{1}{4}×πr^2}$

• 象限圆周 =$\mathrm{\frac{1}{4}×2πr}$

• 象限周长 =$\mathrm{\frac{πr}{2}+2r}$

(注意：计算周长时，应将整个边界加上圆形边界的两倍半径。因为象限由两个圆形部分和两条直线组成，其长度等于半径。)

例如，求半径为10m的圆的象限面积。假设π=3.141。

解 计算象限面积的公式为：

这里，r=10，π=3.141

$$\mathrm{A=\frac{πr^2}{4}=\frac{3.141×(10)^2}{4}=78.525m^2.}$$

例2 求半径为11cm的圆的象限周长。

解：这里，r= 11 cm，计算象限周长的公式为：

$$\mathrm{P=11×\frac{3.141}{2}+2=19.276 cm}$$

圆的象限的性质

• 第一象限是圆的右上角部分。在这个象限中，x坐标和y坐标都是正数。象限中的角度范围从0⁰到90⁰。

• 第二象限是圆的左上角部分。在这个象限中，x坐标为负数，y坐标为正数。象限中的角度范围从90⁰到180⁰。

• 第三象限是圆的左下角部分。在这个象限中，x坐标和y坐标都是负数。象限中的角度范围从180⁰到270⁰。

• 第四象限是圆的右下角部分。在这个象限中，x坐标为正数，y坐标为负数。象限中的角度范围从270⁰到360⁰。

结论

本教程涵盖了笛卡尔平面、笛卡尔平面中的象限、圆和圆的象限及其性质等主题。

常见问题

1. 笛卡尔平面的一些应用是什么？

笛卡尔平面用于确定两点之间的距离、两条分割线的比率以及相交线的中间点。

2. (2, -3) 是否位于第四象限？

是的。(2, -3) 位于第四象限。因为x的值为正，y的值为负。因此，该点应该位于第四象限。

3. 第三象限是正数还是负数？

不是。第三象限中的x坐标和y坐标都是负数。

4. 什么是单位圆？

单位圆是一个半径为一个单位的圆。这个圆大多在笛卡尔和坐标平面上表示。这个圆有助于寻找三角比率的值。

5. 圆的象限和扇区有什么区别？

象限是圆的四分之一，角度为90⁰。扇区是圆的任何角度的划分。