圆的切线

---

简介

圆的切线是指与圆相切于一点的直线。所有与一个固定点等距的点的集合称为圆，而平面上一组连续的点的集合称为直线。在几何学中，如果一条直线与圆在同一平面内，并且在圆周外与圆只有一个交点，即两条线只有唯一的一个交点，那么这条直线就被称为圆的切线。从圆外一点可以画出无数条这样的直线。

圆的切线

与圆周上的恰好一个点相切于同一平面的直线称为圆的切线。直线和圆的唯一公共点称为切点。

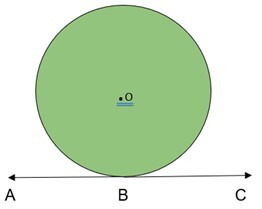
这是一个几何表示，一个以 O 为圆心的圆在一个平面上的点 B 与直线 AC 相交。由于直线和圆的圆周只有一个公共点，因此 AC 成为圆的切线，B 为切点。这条直线位于圆的边界之外。

方程为 x²+y²=a² 的圆在 (p,q) 点处的切线由 p²+q²=a² 给出。

圆的切线的性质

有各种性质定义了在特定点存在圆的切线。下面讨论其中的一些性质：

性质	几何表示
圆的切线在圆周上恰好与圆相切于一点。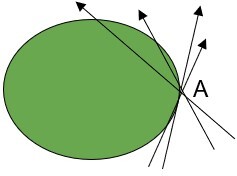
与圆的割线平行的切线只有两条。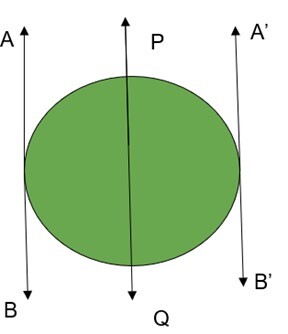
从圆外一点可以画出两条切线到圆。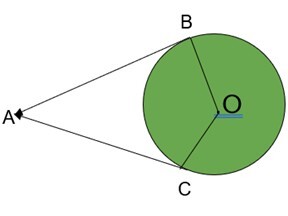

与圆的切线相关的定理

1. 圆上任意一点的切线总是与圆的半径成 90° 角。

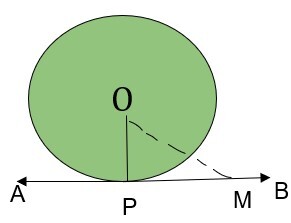
证明：在以 O 为圆心的圆的切线 AB 上取一点 M。因为切线和圆只有一个公共点，即 P，所以该点 M 位于圆外。因此，OM 比 OP（圆的半径）长。

$$\mathrm{OM > OP}$$

这对于 AB 上除 P 之外的所有点都成立。

⇒ OP 是从点 O 到 AB 上任意点的最短距离。

由于垂直距离是点到线的最短距离，所以 OP 垂直于 AB。

2. 从圆外一点画出的两条切线的长度相等。

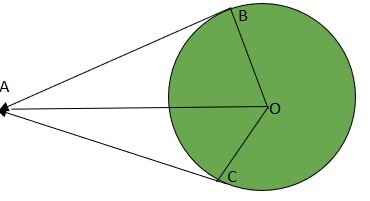
证明：AB=AC

证明：A 是位于以 O 为圆心的圆外的点。AB 和 AC 是从 A 到圆分别在 B 和 C 的两条切线。

由于我们知道圆的切线垂直于半径，

$$\mathrm{∴ ∠OBA=∠OCA}$$

⇒ OBA 和 OCA 是直角三角形。

现在，

在 OBA 和 OBC 中，

OB=OC（圆的半径）

OA=OA（公共边）

$$\mathrm{\angle OBA=\angle OCA=90°}$$

$$\mathrm{∴ △OBA≅△OCA}$$

$$\mathrm{⇒ AB=AC}$$

因此，从圆外一点画出的两条切线的长度相等。

例题

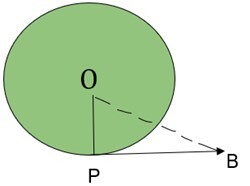
1. 如果圆的半径为 3 厘米，OB = 5 厘米，求切线 PB 的长度（厘米）。

由于 OPB 是一个直角三角形，因为圆的切线在切点处垂直于半径，

$$\mathrm{∴ (OP)^2+(PB)^2=(OB)^2}$$

$$\mathrm{\Rightarrow (3)^2+(PB)^2=(5)^2}$$

$$\mathrm{\Rightarrow (PB)^2=(5)^2-(3)^2}$$

$$\mathrm{\Rightarrow (PB)^2=16}$$

$$\mathrm{\Rightarrow PB=4cm}$$

2. 在给定图形中，以 O 为圆心的圆在 A 和 B 处与∠ACB 的边相切。如果∠BAC=80°，求∠BOC 的度数。

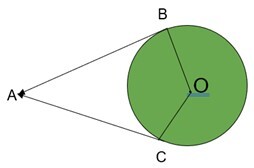
$$\mathrm{\angle BAC+\angle ACO+\angle COB+\angle OBA=360°}$$

这是因为四边形的内角和等于 360°。

$$\mathrm{80°+90°+90°+ \angle BOC= 360°}$$

$$\mathrm{\angle BOC=100°}$$

3. 在给定图形中，∠BOC=140°，求∠BAC。

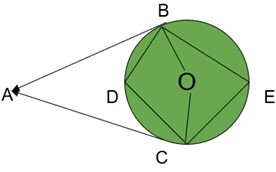
由于圆内角的大小是形成相同弧的圆心角大小的一半，

因此，

$$\mathrm{\angle BEC=1/2 \angle BOC}$$

$$\mathrm{\Rightarrow \angle BEC=70°}$$

现在，

$$\mathrm{\angle BAC+\angle ACO+\angle COB+\angle OBA=360°}$$

$$\mathrm{\Rightarrow \angle BAC=360°-90°-90°-70°}$$

$$\mathrm{\Rightarrow \angle BAC=110°}$$

结论

本教程将圆的切线描述为一条直线与圆在同一平面内相交的唯一公共点。一个圆可以有无限多条切线，但是从一个点只能画出一条切线到圆。切线垂直于圆的半径，即它与半径成 90° 角。切线与圆相切的点称为切点。圆的切线是一个有价值的信息，因为它使我们能够找出曲线在特定点处的曲线的斜率。方程为 x²+y²=a² 的圆在 (p,q) 点处的切线由 p²+q²=a² 给出。

常见问题

1. 两个圆可以相互相切吗？

切线是与圆相切于恰好一点的直线。因此，如果一个圆在同一平面上与另一个圆恰好相切于一点，那么它们有一个共同点，因此，一个圆在该点与另一个圆相切。

2. 从圆周上一点和圆外一点可以画出的切线的数量有什么区别？

从圆周上一点只能画出一条切线，因为切线与圆恰好相切于一点。但是，从圆外一点可以画出两条切线到圆，每条切线都与圆相切于一点。

3. 给出圆的切线的两个现实生活中的例子。

• 自行车轮胎是一个在平面道路上行驶的圆，其中道路在轮胎上的每个点形成一个切线，因为自行车在移动。

• 球在跷跷板上滚动是另一个例子，其中跷跷板的表面在球滚下跷跷板时在球上的每个点都是切线。

4. 圆心与其切线之间的最小距离是多少？

圆心与其切线之间的最小距离是圆的半径，因为切线上圆外的任何其他点都位于圆的边界之外，这意味着它大于圆的半径。

5. 切线可以是割线吗？

圆的切线可以是割线的一种特殊情况，其中其相应弦的两端点重合。