如果 PT 是一个圆的切线，该圆的圆心为 O，且 $OP = 17\ cm$，$OT = 8\ cm$。求切线段 PT 的长度。

---

已知

PT 是一个圆的切线，该圆的圆心为 O，且 $OP = 17\ cm$，$OT = 8\ cm$。

要求

我们必须找到切线段 PT 的长度。

解答

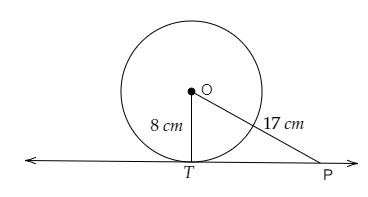
$OP = 17\ cm$ 且 $OT = 8\ cm$

$PT$ 是圆在 $T$ 点的切线。

$OT\ perp\ PT$

在直角三角形 $OTP$ 中，

根据勾股定理，

$OP^2= OT^2+ TP^2$

$17^2 = 8^2 + TP^2$

$TP^2= 289 - 64$

$= 225$

$= 15^2$

因此，

$TP = 15\ cm$

切线段 PT 的长度为 15 cm。