圆形扇形的面积

---

介绍

圆形扇形的面积是指扇形边界内包围的面积大小。在本教程中，我们将学习圆形扇形以及如何计算圆形扇形的面积。

圆形扇形的面积是指扇形边界内包围的面积大小。

扇形总是从圆心开始。扇形的面积定义为圆内由两条半径及其相邻弧线所围成的部分。半圆是圆中最常见的扇形，它代表半个圆。在本文的后续部分，我们将学习更多关于面积、面积公式以及如何使用弧度和角度计算扇形面积的内容。

我们还将通过一些例子来更好地理解这些主题。

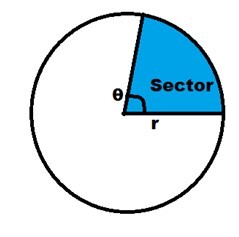
圆形扇形

扇形被认为是圆的一部分，它有两条半径和一条弧。圆被分成两个扇形，一个叫小扇形，另一个叫大扇形。小扇形是圆形较小的一部分，大扇形是圆形较大的部分。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

圆形扇形的面积

• 使用扇形面积公式来计算扇形包围的总面积。扇形的面积可以使用以下公式计算：

  $$\mathrm{扇形面积 =\frac{θ}{360^\circ} × πr^2}$$

  其中 θ 是圆心角（以度为单位），r 是圆的半径。

• 圆形扇形面积 =$\mathrm{\frac{1}{2} × r^2 θ }$，其中 θ 是圆心角（以弧度为单位），r 是圆的半径。

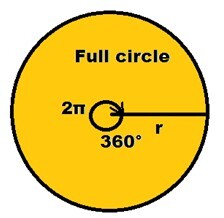
• 让我们推导出圆形扇形面积的公式。我们知道一个完整的圆是 360 度。圆心角为 360° 的圆的面积为 πr²，其中 r 是圆的半径。

• 如果圆心角为 1°，则扇形的面积为 $\mathrm{\frac{ πr^2}{360°}}$。因此，如果圆心角为 θ，则扇形的面积 =$\mathrm{=(\frac{θ}{360°})\times πr^2}$，其中 θ 是圆心角（以度为单位），r 是圆的半径。

• 换句话说，πr² 表示整个圆的面积，而 $\mathrm{\frac{θ}{360°}}$ 表示扇形覆盖了圆的多少比例。

扇形公式

如果圆心角 θ 以弧度表示，则

$$\mathrm{扇形面积 = \frac{1}{2} × r^2 θ,}$$

其中 θ 是圆心角（以弧度为单位），r 是圆的半径。

需要注意的是，半圆和象限是特殊的扇形，其角度分别为 180° 和 90°。

例题

1) 半径为 6，圆心角为 60° 的圆形扇形的面积是多少？

答：扇形的面积$\mathrm{=(\frac{θ}{360°}) × πr^2=(\frac{60°}{360°}) × π.6^2=6π}$

因此，面积是 6π。

2) 半径为 5，圆心角为 120° 的圆形扇形的面积是多少？

答：扇形的面积$\mathrm{=(\frac{θ}{360°}) × πr^2=(\frac{120°}{360°}) × π.5^2=8.3π}$

因此，面积是 8.3π。

结论

在本教程中，我们学习了圆形扇形及其面积的计算。扇形表示圆的一部分的面积。我们知道圆的面积用公式 πr² 计算。我们知道一个完整的圆是 360 度。圆心角为 360° 的圆的面积为 πr²，其中 r 是圆的半径。如果圆心角为 1°，则面积为 $\mathrm{\frac{πr^2}{360°}}$。因此，如果圆心角为 θ，则扇形的面积 =$\mathrm{(\frac{θ}{360°})\times πr^2}$，其中 θ 是圆心角（以度为单位），r 是圆的半径。我们还使用扇形面积公式解答了一些例题。

常见问题

1. 什么是圆形扇形的面积？

扇形所包围的圆形空间称为扇形的面积。圆内由两条半径及其相邻弧线所围成的部分称为扇形。

2. 计算圆形扇形面积的方法是什么？

计算扇形面积的两个主要公式是：其中 r 是圆的半径。

$$\mathrm{圆形扇形面积 =\frac{1}{2} × r^2 θ,}$$

其中 θ 是圆心角（以弧度为单位），r 是圆的半径。

3. 圆形扇形是什么意思？

扇形定义为圆内由两条半径及其相邻弧线所围成的部分。半圆是圆中最常见的扇形，代表半个圆。

4. 弧线是什么意思？

曲线的一部分或圆的一部分称为弧线。许多物体的形状都包含曲线。这些物体的曲线部分在数学上称为弧线。

5. 如何根据弧长和半径计算扇形的面积？

给定弧长和半径，您可以计算扇形的面积。首先，使用公式弧长 $\mathrm{=(\frac{θ}{360° }) × πr^2}$ 计算弧度（θ）。现在您知道了半径。知道了角度，您可以使用以下公式计算扇形的面积：

$$\mathrm{圆形扇形面积 =(\frac{θ}{360° }) × πr^2}$$

6. 如何根据扇形的面积求半径？

您可以通过将值代入公式来计算半径：

$$\mathrm{圆面积 =(\frac{θ}{360° }) × πr^2}$$

将给定值代入公式，面积 $\mathrm{= (\frac{θ}{360° }) × πr^2}$，即 $\mathrm{H.36π = (\frac{90}{360} × πr^2}$，得出 r²=144，这意味着 r = 12 个单位。

7. 如何用π表示扇形的面积？

扇形面积也可以用 π 表示。例如，如果圆的半径为 4 个单位，扇形的圆心角为 90°，让我们用 π 计算扇形的面积。扇形面积 = $\mathrm{=(\frac{θ}{360°}) × πr^2 }$。将值代入等式，扇形的面积 $\mathrm{= (\frac{90}{360}) × π×4^2 }$，计算结果为面积为 4π。

8. 如何用弧度计算扇形的面积？

要查找圆心角为弧度的扇形的面积，请使用公式

$$\mathrm{面积 =\frac{1}{2} × r^2 θ, }$$

其中 θ 是圆心角（以弧度为单位），r 是圆的半径。