数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学
正确答案：$(c)$ 大幅增加 短路：短路是指电流经常通过电阻非常低的电路的情况。短路示例：当电池的正负极连接到细导线（电阻非常低）时，就可以看到短路发生的常见示例。由于连接处的电阻非常低，因此会通过高电流，从而使电池能够在短时间内释放大量能量。结论：连接处的电阻过低是… 阅读更多
"
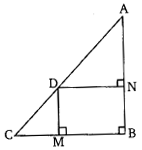
已知：$AD$ 是三角形 $ABC$ 的中线，$AM \perp BC$。 要证明：$\mathrm{AB}^{2}=\mathrm{AD}^{2}-\mathrm{BC} \times \mathrm{DM}+(\frac{\mathrm{BC}}{2})^2$ 证明：在 $\triangle \mathrm{AMB}$ 中，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{BM}^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\mathrm{BD}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\frac{\mathrm{BC}}{2}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{MD}^{2}+(\frac{\mathrm{BC}}{2})^{2}-\frac{2 \mathrm{BC}}{2} \times \mathrm{MD}$$\mathrm{AB}^{2}=(\mathrm{AM}^{2}+\mathrm{MD}^{2})+(\frac{\mathrm{BC}}{2})^{2}-\mathrm{BC} \times \mathrm{MD}$$\mathrm{AB}^{2}=\mathrm{AD}^{2}-\mathrm{BC} \times \mathrm{MD}+(\frac{\mathrm{BC}}{2})^{2}$ 证毕。阅读更多
已知：$AD$ 是三角形 $ABC$ 的中线，$AM \perp BC$。要证明：$\mathrm{AC}^{2}+\mathrm{AB}^{2}=2 \mathrm{AD}^{2}+\frac{1}{2} \mathrm{BC}^{2}$ 证明：在 $\triangle \mathrm{AMC}$ 中，$\angle \mathrm{AMC}=90^{\circ}$ 因此，根据勾股定理，$\mathrm{AC}^{2}=\mathrm{AM}^{2}+\mathrm{MC}^{2}$$\mathrm{AC}^{2}=\mathrm{AM}^{2}+(\mathrm{MD}^{2}+\mathrm{DC}^{2})$ ($\mathrm{MC}=\mathrm{MD}+\mathrm{DC}$)$\mathrm{AC}^{2}=\mathrm{AM}^{2}+(\mathrm{MD}+\frac{1}{2} \mathrm{BC})^{2}$$\mathrm{AC}^{2}=\mathrm{AM}^{2}+\mathrm{MD}^{2}+(\frac{\mathrm{BC}}{2})^{2}+2 \mathrm{MD} \times \frac{\mathrm{BC}}{2}$$\mathrm{AC}^{2}=(\mathrm{AM}^{2}+\mathrm{MD}^{2})+\mathrm{MD} \times \mathrm{BC}+(\frac{\mathrm{BC}}{2})^{2}$$\mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{MD} \times \mathrm{BC}+(\frac{\mathrm{BC}}{2})^{2}$......(i) 在 $\triangle \mathrm{AMB}$ 中，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{BM}^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\mathrm{BD}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\frac{\mathrm{BC}}{2}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{MD}^{2}+(\frac{\mathrm{BC}}{2})^{2}-\frac{2 \mathrm{BC}}{2} \times \mathrm{MD}$$\mathrm{AB}^{2}=(\mathrm{AM}^{2}+\mathrm{MD}^{2})+(\frac{\mathrm{BC}}{2})^{2}-\mathrm{BC} \times \mathrm{MD}$$\mathrm{AB}^{2}=\mathrm{AD}^{2}-\mathrm{BC} \times \mathrm{MD}+(\frac{\mathrm{BC}}{2})^{2}$.........(ii) 将式 (i) 和 (ii) 相加，得到 $AC^{2}+AB^{2}=2AD^{2}+\frac{2 BC^{2}}{4}$$AC^{2}+AB^{2}=2AD^{2}+\frac{BC^{2}}{2}$ 证毕。阅读更多
证明：平行四边形的对角线互相平分。设 $ABCD$ 是一个平行四边形，对角线 $AC$ 和 $BD$ 相交于 $O$。这意味着 $BO$ 和 $DO$ 分别是三角形 $ABC$ 和 $ADC$ 的中线。$\mathrm{AB}^{2}+\mathrm{BC}^{2}=2 \mathrm{BO}^{2}+\frac{1}{2} \mathrm{AC}^{2}$...........(i)$\mathrm{AD}^{2}+\mathrm{CD}^{2}=2 \mathrm{OD}^{2}+\frac{1}{2} \mathrm{AC}^{2}$...........(ii) 将 (i) 和 (ii) 相加，得到 $\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}+\mathrm{AD}^{2}=2(\mathrm{BO}^{2}+\mathrm{OD}^{2})+\mathrm{AC}^{2}$$=2(\frac{1}{4} \mathrm{BD}^{2}+\frac{1}{4} \mathrm{BD}^{2})+\mathrm{AC}^{2}$ (因为 $\mathrm{DO}=\mathrm{BO}=\frac{1}{2} \mathrm{BD}$)$=2 \times \frac{1}{2} \mathrm{BD}^{2}+\mathrm{AC}^{2}$$\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}+\mathrm{AD}^{2}=\mathrm{AC}^{2}+\mathrm{BD}^{2}$ 证毕。 阅读更多
"
已知：$AD$ 是三角形 $ABC$ 的中线，$AM \perp BC$。 要证明：(i) $\mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{BC} \times \mathrm{DM}+(\frac{\mathrm{BC}}{2})^{2}$(ii) $\mathrm{AB}^{2}=\mathrm{AD}^{2}-\mathrm{BC} \times \mathrm{DM}+(\frac{\mathrm{BC}}{2})^2$(iii) $\mathrm{AC}^{2}+\mathrm{AB}^{2}=2 \mathrm{AD}^{2}+\frac{1}{2} \mathrm{BC}^{2}$ 证明：(i) 在 $\triangle \mathrm{AMC}$ 中，$\angle \mathrm{AMC}=90^{\circ}$ 因此，根据勾股定理，$\mathrm{AC}^{2}=\mathrm{AM}^{2}+\mathrm{MC}^{2}$$\mathrm{AC}^{2}=\mathrm{AM}^{2}+(\mathrm{MD}^{2}+\mathrm{DC}^{2})$ ($\mathrm{MC}=\mathrm{MD}+\mathrm{DC}$)$\mathrm{AC}^{2}=\mathrm{AM}^{2}+(\mathrm{MD}+\frac{1}{2} \mathrm{BC})^{2}$$\mathrm{AC}^{2}=\mathrm{AM}^{2}+\mathrm{MD}^{2}+(\frac{\mathrm{BC}}{2})^{2}+2 \mathrm{MD} \times \frac{\mathrm{BC}}{2}$$\mathrm{AC}^{2}=(\mathrm{AM}^{2}+\mathrm{MD}^{2})+\mathrm{MD} \times \mathrm{BC}+(\frac{\mathrm{BC}}{2})^{2}$$\mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{MD} \times \mathrm{BC}+(\frac{\mathrm{BC}}{2})^{2}$ 证毕。(ii) 在 $\triangle \mathrm{AMB}$ 中，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{BM}^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\mathrm{BD}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\frac{\mathrm{BC}}{2}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{MD}^{2}+(\frac{\mathrm{BC}}{2})^{2}-\frac{2 \mathrm{BC}}{2} \times \mathrm{MD}$$\mathrm{AB}^{2}=(\mathrm{AM}^{2}+\mathrm{MD}^{2})+(\frac{\mathrm{BC}}{2})^{2}-\mathrm{BC} \times \mathrm{MD}$$\mathrm{AB}^{2}=\mathrm{AD}^{2}-\mathrm{BC} \times \mathrm{MD}+(\frac{\mathrm{BC}}{2})^{2}$ 证毕。(iii) 在 $\triangle \mathrm{AMC}$ 中，$\angle \mathrm{AMC}=90^{\circ}$ 因此，根据勾股定理，$\mathrm{AC}^{2}=\mathrm{AM}^{2}+\mathrm{MC}^{2}$$\mathrm{AC}^{2}=\mathrm{AM}^{2}+(\mathrm{MD}^{2}+\mathrm{DC}^{2})$ ($\mathrm{MC}=\mathrm{MD}+\mathrm{DC}$)$\mathrm{AC}^{2}=\mathrm{AM}^{2}+(\mathrm{MD}+\frac{1}{2} \mathrm{BC})^{2}$$\mathrm{AC}^{2}=\mathrm{AM}^{2}+\mathrm{MD}^{2}+(\frac{\mathrm{BC}}{2})^{2}+2 \mathrm{MD} \times \frac{\mathrm{BC}}{2}$$\mathrm{AC}^{2}=(\mathrm{AM}^{2}+\mathrm{MD}^{2})+\mathrm{MD} \times \mathrm{BC}+(\frac{\mathrm{BC}}{2})^{2}$$\mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{MD} \times \mathrm{BC}+(\frac{\mathrm{BC}}{2})^{2}$......(i) 在 $\triangle \mathrm{AMB}$ 中，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{BM}^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\mathrm{BD}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+(\frac{\mathrm{BC}}{2}-\mathrm{MD})^{2}$$\mathrm{AB}^{2}=\mathrm{AM}^{2}+\mathrm{MD}^{2}+(\frac{\mathrm{BC}}{2})^{2}-\frac{2 \mathrm{BC}}{2} \times \mathrm{MD}$$\mathrm{AB}^{2}=(\mathrm{AM}^{2}+\mathrm{MD}^{2})+(\frac{\mathrm{BC}}{2})^{2}-\mathrm{BC} \times \mathrm{MD}$$\mathrm{AB}^{2}=\mathrm{AD}^{2}-\mathrm{BC} \times \mathrm{MD}+(\frac{\mathrm{BC}}{2})^{2}$.........(ii) 将式… 阅读更多
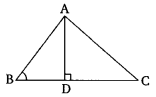
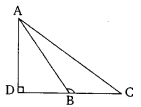
在给定图形中，$ABC$ 是一个三角形，其中 $\angle ABC = 90^o$，并且 $AD \perp CB$。证明 $AC^2 = AB^2 + BC^2 - 2BC \times BD$
"
已知：$ABC$ 是一个三角形，其中 $\angle ABC = 90^o$，并且 $AD \perp CB$。 要证明：$AC^2 = AB^2 + BC^2 - 2BC \times BD$ 证明：在 $\triangle \mathrm{ADB}$ 中，$\angle \mathrm{ADB}=90^{\circ}$ 因此，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{AD}^{2}+\mathrm{BD}^{2}$.........(i) 在 $\triangle \mathrm{ADC}$ 中，$\angle \mathrm{ADC}=90^{\circ}$ 因此，根据勾股定理，$\mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{CD}^{2}$$=\mathrm{AD}^{2}+(\mathrm{BC}^{2}-\mathrm{BD})^{2}$$=\mathrm{AD}^{2}+\mathrm{BC}^{2}+\mathrm{BD}^{2}-2 \mathrm{BC} \times \mathrm{BD})$$=(\mathrm{AD}^{2}+\mathrm{BD}^{2})+\mathrm{BC}^2-2 \mathrm{BC} \times \mathrm{BD}$$=\mathrm{AB}^{2}+\mathrm{BC}^{2}-2 \mathrm{BC} \times \mathrm{BD}$ [根据 (i)] 证毕。阅读更多
"
"
…阅读更多
(ii) △…阅读更多
当田地里的土壤高度酸化时，可以用生石灰或熟石灰等物质进行处理。这些物质呈碱性，可以与土壤中多余的酸反应，降低土壤的酸度。