数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：三块金属立方体的棱长之比为 \( 3: 4: 5 \)，将它们熔化后铸成一个对角线长为 \( 12 \sqrt{3} \mathrm{~cm} \) 的立方体。求：这三块立方体的棱长。解：设三块立方体的棱长分别为 $3x, 4x$ 和 $5x$，熔化后形成的立方体边长为 $a$。熔化后立方体的体积为 $= (3x)^3+ (4x)^3+ (5x)^3$$= 27x^3+64x^3+125x^3$$=216x^3$因此， $a^3= 216x^3$$a^3 = (6x)^3$$\Rightarrow a=6x$立方体的对角线 $=\sqrt{3} a$这意味着， $\sqrt{3} a=12 \sqrt{3}$$a=12$$a=6x=12$$x=2$$\Rightarrow 3x=3(2)=6\ cm$$\Rightarrow 4x=4(2)=8\ cm$$\Rightarrow 5x=5(2)=10\ cm$因此，… 阅读更多
已知：一个半径为 \( 10.5 \mathrm{~cm} \) 的实心金属球体被熔化并重铸成若干个较小的圆锥体，每个圆锥体的半径为 \( 3.5 \mathrm{~cm} \)，高为 \( 3 \mathrm{~cm} \)。求：形成的圆锥体的数量。解：金属球体的半径 $R=10.5\ cm$每个圆锥体的半径 $r=3.5\ cm$每个圆锥体的高 $h=3\ cm$这意味着，实心金属球体的体积 $=\frac{4}{3} \pi R^3$$=\frac{4}{3} \pi (10.5)^3$每个圆锥体的体积 $=\frac{1}{3} \pi r^2 h$形成的圆锥体数量 = 实心金属球体的体积 ÷ 每个圆锥体的体积$=\frac{\frac{4}{3} \pi \times 10.5 \times 10.5 \times ... 阅读更多
已知：一个金属球体的直径为 \( 9 \mathrm{~cm} \)。将其熔化后拉成一根直径为 \( 2 \mathrm{~mm} \) 的长细线，细线横截面均匀。求：细线的长度。解：金属球体的直径 $=9 \mathrm{~cm}$这意味着，球体的半径 $r=\frac{9}{2} \mathrm{~cm}$球体的体积 $=\frac{4}{3} \pi r^{3}$$=\frac{4}{3} \pi(\frac{9}{2})^{3}$$=\frac{243}{2} \pi \mathrm{cm}^{3}$细线的直径 $=2 \mathrm{~mm}$这意味着，细线的半径 $=\frac{2}{2} \mathrm{~mm}$$=1 \mathrm{~mm}$$=\frac{1}{10} \mathrm{~cm}$设细线的长度为 $h$，这意味着， $\pi r^{2} h=\frac{243}{2} \pi$$\Rightarrow r^{2} h=\frac{243}{2}$$\Rightarrow (\frac{1}{10})^{2} h=\frac{243}{2}$$\Rightarrow \frac{1}{100} h=\frac{243}{2}$$\Rightarrow h=\frac{243}{2} \times 100$$\Rightarrow h=12150 \mathrm{~cm}$细线… 阅读更多
已知：一个铁球被熔化并重铸成许多大小相同的较小铁球。每个较小铁球的半径是原铁球半径的 \( 1 / 4 \)。求：能铸成多少个这样的较小铁球？比较所有较小铁球的表面积总和与原铁球的表面积。解：设原铁球的半径为 $R$。这意味着，每个较小铁球的半径 $r=\frac{1}{4} \mathrm{R}$原铁球的体积 $V_1=\frac{4}{3} \pi \mathrm{R}^{3}$每个较小铁球的体积 $V_2=\frac{4}{3} \pi r^{3}$$=\frac{4}{3} \pi(\frac{1}{4} \mathrm{R})^{3}$$=\frac{1}{64} \times \frac{4}{3} \pi \mathrm{R}^{3}$铁球的数量… 阅读更多
已知：一个半径为 \( 3 \mathrm{~cm} \) 的铜球被熔化并重铸成一个高为 3 \( \mathrm{cm} \) 的直圆锥体。求：圆锥体底部的半径。解：铜球的半径 $r=3 \mathrm{~cm}$铜球的体积 $=\frac{4}{3} \pi r^{3}$$=\frac{4}{3} \pi \times(3)^{3}$$=36 \pi \mathrm{cm}^{3}$由铜球形成的圆锥体的体积 = 铜球的体积 $=36 \pi \mathrm{cm}^{3}$圆锥体的高 $h=3 \mathrm{~cm}$设圆锥体的半径为 $R$。因此， $\frac{1}{3} \pi R^{2} h=36 \pi$$\Rightarrow \frac{1}{3} R^{2}(3)=36 \pi$$\Rightarrow \pi R^{2}=36 \pi$$\Rightarrow R^{2}=36$$\Rightarrow R^{2}=(6)^{2}$$\Rightarrow R=6\ cm$圆锥体的半径是 $6 ... 阅读更多
已知：一根直径为 \( 1 \mathrm{~cm} \)，长为 \( 8 \mathrm{~cm} \) 的铜棒被拉成一根长为 \( 18 \mathrm{~m} \) 的均匀粗细的细线。求：细线的粗细。解：铜棒的直径 $=1 \mathrm{~cm}$这意味着，圆锥体的半径 $\mathrm{R}=\frac{1}{2} \mathrm{~cm}$圆锥体的高 $H=8 \mathrm{~cm}$因此，圆锥体的体积 $=\pi \mathrm{R}^{2} H$$=\pi \times(\frac{1}{2})^{2} \times 8 \mathrm{~cm}^{3}$$=\pi \times \frac{1}{4} \times 8$$=2 \pi \mathrm{cm}^{3}$拉成的细线的长度 $h=18 \mathrm{~m}$$=1800 \mathrm{~cm}$设细线的半径为 $r$。因此，细线的体积 $=\pi r^{2} h$$=\pi r^{2} \times 1800$$\Rightarrow 1800 ... 阅读更多
已知：一个空心球壳的内外表面直径分别为 \( 10 \mathrm{~cm} \) 和 \( 6 \mathrm{~cm} \)。如果将其熔化并重铸成一个长为 \( 2 \frac{2}{3} \mathrm{~cm} \) 的实心圆柱体。求：圆柱体的直径。解：球体外表面的直径 $=10 \mathrm{~cm}$球体的内径 $=6 \mathrm{~cm}$因此，外半径 $\mathrm{R}=\frac{10}{2}$$=5 \mathrm{~cm}$内半径 $r=\frac{6}{2}$$=3 \mathrm{~cm}$所用金属的体积 $=\frac{4}{3} \pi[\mathrm{R}^{3}-r^{3}]$$=\frac{4}{3} \pi[5^{3}-3^{3}]$$=\frac{4}{3} \pi(125-27)$$=\frac{4}{3} \pi \times 98$$=\frac{392 \pi}{3} \mathrm{~cm}^{3}$因此，形成的实心圆柱体的体积 $=\frac{392}{3} \pi \mathrm{cm}^{3}$圆柱体的长度 $h=2 \frac{2}{3} \mathrm{~cm}$$=\frac{8}{3} ... 阅读更多
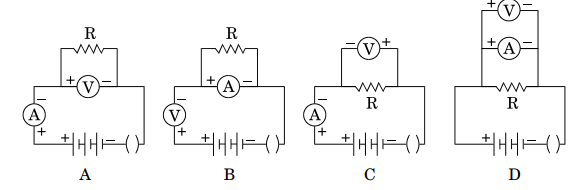
"\在给定的图中，研究电流对电阻两端电压依赖性的正确装置是选项 (c)。这是正确的，因为在这个测定电流对电阻两端电压依赖性的实验中，电压表与电阻并联连接，电流表与电阻串联连接。此外，电流表和电压表的极性标记正确。
学生在追踪光线穿过玻璃棱镜的路径时，应该注意的四个预防措施如下：1. 确保所取的棱镜是抛光的，没有破损。2. 确保通过棱镜观察图像时，视线处于正确的水平位置。3. 应该使用锋利的铅笔绘制玻璃棱镜的边界，以便绘制清晰的线条来观察正确的结果。4. 入射角理想情况下应为 45°，以获得更好的结果。说明在一个实验中，追踪光线穿过玻璃棱镜的路径，针对不同的…… 阅读更多
力改变运动的方向。说明作用于物体的力可能会改变物体的速度、形状和运动方向。