数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究
题目：解答：$72\div 12$。解答：如题所示，$72\div 12$$=\frac{72}{12}$$=\frac{12\times6}{12}$$=6$因此，$72\div 12=6$。
已知：一个数 $61254$。题目：求最小的数，使给定数字乘以这个数后得到一个完全立方数。解答：给定数字$=61254$对给定数字进行因数分解，$6125=\underline{5\times5\times5}\times7\times7$当给定数字乘以 $7$ 时，它变为：$6125\times7=42875$$42875=35\times35\times35$因此，给定数字 $6125$ 必须乘以 $7$ 才能成为完全立方数。
已知：一个数：$900$。题目：求最小的数，使给定数字乘以这个数后得到一个完全立方数。解答：给定数字：$900$对给定数字进行因数分解：$900=\underline{2\times2}\times\underline{5\times5}\times\underline{3\times3}$因此，所需的数字是$=2\times5\times3$$=30$因此，给定数字 $900$ 必须乘以 $30$ 才能使其成为完全立方数。
已知：一条长度为 12 厘米的线段。题目：我们必须确定一个点，将一条长度为 12 厘米的线段以 $2 : 3$ 的比例内分。解答：作图步骤：(i) 画一条线段 $AB = 12\ cm$。(ii) 在 $A$ 点画一条射线 $AX$，与 $AB$ 成锐角。(iii) 从 $B$ 点画另一条射线 $BY$，平行于 $AX$。(iv) 从 $AX$ 上截取两个相等的部分，从 $BY$ 上截取三个相等的部分。(v) 连接 $A_2$ 和 $B_3$，它们相交于 $AB$ 上的点 $P$。$P$ 是所需的点，它将 $AB$ 以 $2 : 3$ 的比例内分。依据：在 $\triangle \mathrm{AA}_{2} ... 阅读更多
"\解答：数字23456891011128是/否是/否是/否否是/否否否否990是/否是/否是/否是/否是/否是1586是/否否否否否否否否275否否否是/否否否是6686是/否否否否否否否否639210是/否是/否是/否否是/否是429714是/否否否否否否否否2856是/否是/否是/否否否否3060是/否是/否是/否是/否是406839否是/否否否否否否否
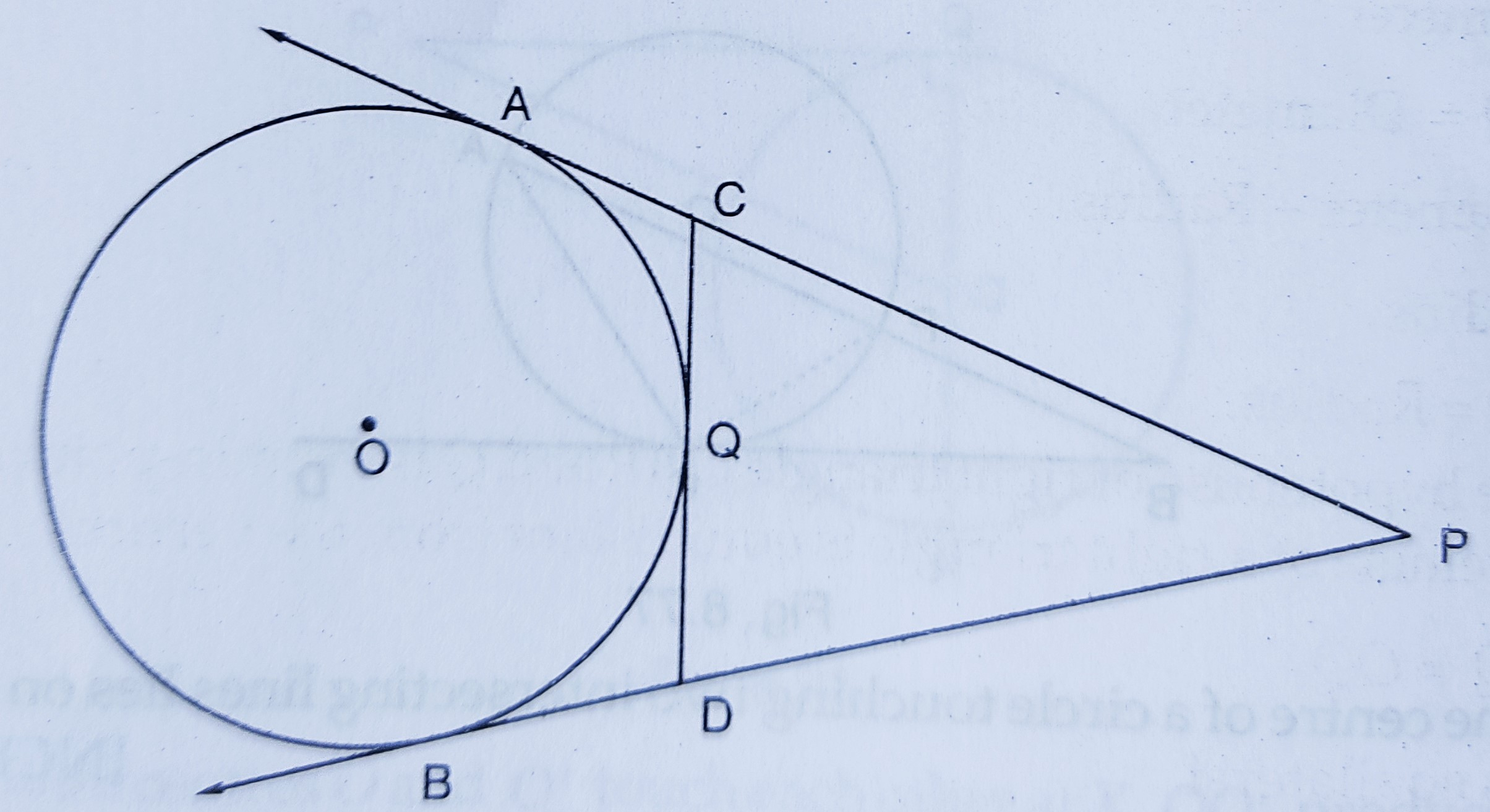
"\已知：如图，\( P A \) 和 \( P B \) 是从外一点 \( P \) 到圆的切线。\( C D \) 是另一条切线，在 \( Q \) 点与圆相切。\( PA=12\ cm, QC=QD=3\ cm. \)题目：我们必须求 \( P C+P D \)。解答：我们知道，从外一点引出的切线相等。这意味着，$PA = PB = 12\ cm$.....…(i)$QC = AC = 3\ cm$......(ii)$QD = BD = 3\ cm$.......(iii)因此，$PC + PD = (PA - AC) + (PB - BD)$$= (12 - 3) + (12 - 3)$ [根据 (i)、(ii) 和 (iii)]$= 9 + 9$$= 18\ cm$因此，\( P C+P D = 18\ cm \)。
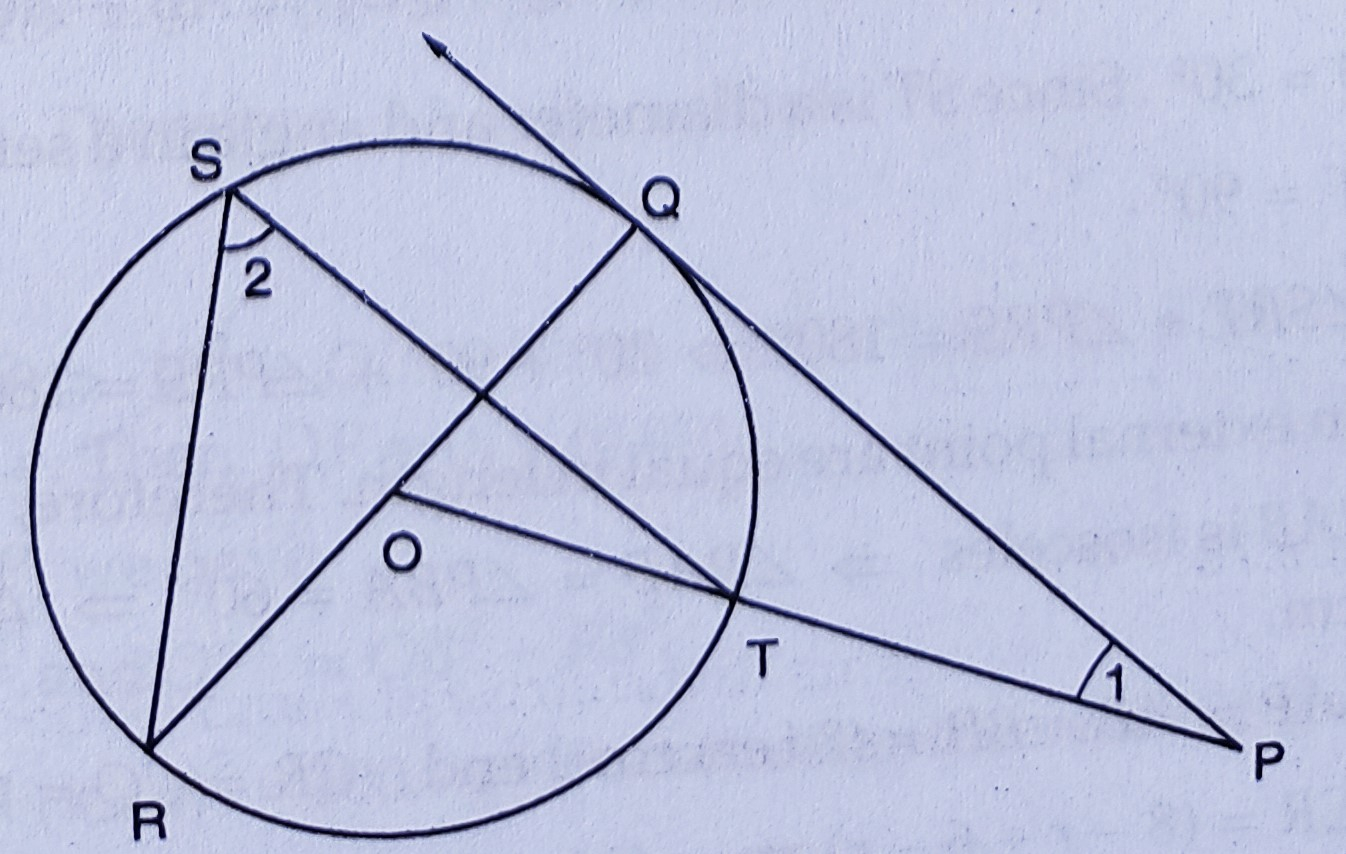
"\已知：如图，\( P Q \) 是从外一点 \( P \) 到以 \( O \) 为圆心的圆的切线，\( O P \) 与圆相交于 \( T \) 点，\( Q O R \) 是直径。\( \angle P O R=130^{\circ} \) 且 \( S \) 是圆上的一个点。题目：我们必须求 \( \angle 1+\angle 2 \)。解答：连接 $RT$。 $\angle POR = 130^o$$\angle POQ = 180^o- \angle POR$ $= 180^o - 130^o$ $= 50^o$$PQ$ 是圆的切线。$\angle PQO = 90^o$在 $\triangle ... 阅读更多
已知：与两条相交直线相切的圆的圆心。题目：我们必须证明与两条相交直线相切的圆的圆心位于这两条直线的角平分线上。解答：设从外一点 $P$ 到以 $O$ 为圆心的圆引出两条切线 $PQ$ 和 $PR$。连接 $OR$ 和 $OQ$。在 $\triangle POR$ 和 $\triangle POQ$ 中， $\angle PRO = \angle PQO = 90^o$ （圆上任意一点的切线垂直于过该切点的半径）$OR = OQ$ （圆的半径）$OP = OP$ （公共边）因此，根据 RHS 全等，$\triangle PRO\ ... 阅读更多
"\**已知：**图中，有两个同心圆，圆心为 O。PR T 和 PQS 是从外圆上一点 P 引到内圆的两条切线。PR=5 cm。**求：**我们要求 PS 的长度。**解：**连接 OS 和 OP。在△POS 中，PO = OS这表明，△POS 是一个等腰三角形。我们知道，在一个等腰三角形中，如果从等腰的公共顶点向底边作垂线，那么这条线将平分… 阅读更多
**已知：** 99×13=(100-1)×13=… … … … **求：**求解：99×13=(100-1)×13=… … … … **解：** 99×13 =(100-1)×13 =1300-13=1287 [∵ (a-b)x=ax-bx 根据分配律] 因此，99×13=(100-1)×13=1287。