数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：一个八边形。 求解：求正八边形的内角和外角之比。解：正八边形的每个外角 = 360/8 = 45° 正八边形的每个内角 = (180° - 45°) = 135° 因此，八边形的内角和外角之比 = 135°/45° = 3/1 = 3:1
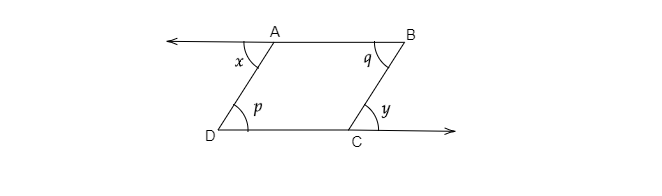
已知：在给定图形中，两条横截线与两条平行线 AB 和 CD 相交。求解：检查是否 x+y=p+q。解：已知，当一条横截线与两条平行线相交时，内错角相等。=> ∠x = ∠p … (i) 同样地，∠y = ∠q … (ii) 将 (i) 和 (ii) 相加，∠x + ∠y = ∠x + ∠y
已知：$\frac{4 \sqrt{3}+5 \sqrt{2}}{\sqrt{48}+\sqrt{18}}$。求解：化简 $\frac{4 \sqrt{3}+5 \sqrt{2}}{\sqrt{48}+\sqrt{18}}$。解：如题所示 $\frac{4\sqrt{3}+5\sqrt{2}}{\sqrt{48}+\sqrt{18}}$ = $\frac{4\sqrt{3}+5\sqrt{2}}{4\sqrt{3}+3\sqrt{2}}$ [∵ √48=4√3 和 √18=3√2] 将分子和分母都乘以 4√3-3√2 =$\frac{4\sqrt{3}+5\sqrt{2}}{4\sqrt{3}+3\sqrt{2}}\times\frac{4\sqrt{3}-3\sqrt{2}}{4\sqrt{3}-3\sqrt{2}}$ =$\frac{( 4\sqrt{3}+5\sqrt{2})(4\sqrt{3}-3\sqrt{2})}{( 4\sqrt{3})^2-( 3\sqrt{2})^2}$=$\frac{48+20\sqrt{6}-12\sqrt{6}-30}{48-18}$=$\frac{18+8\sqrt{6}}{30}$ =$\frac{2( 9+4\sqrt{6})}{30}$=$\frac{9+4\sqrt{6}}{15}$ 因此，$\frac{4 \sqrt{3}+5 \sqrt{2}}{\sqrt{48}+\sqrt{18}}=\frac{9+4\sqrt{6}}{15}$。
已知：$3\sqrt{3}+2\sqrt{27}+\frac{7}{\sqrt{3}}$。求解：解方程 $3\sqrt{3}+2\sqrt{27}+\frac{7}{\sqrt{3}}$。解：$2\sqrt{27} =2\sqrt{3\times3\times3}=6\sqrt{3}$ $\frac{7}{\sqrt{3}}=\frac{(7\times\sqrt{3})}{(\sqrt{3}\times\sqrt{3})}=\frac{7\sqrt{3}}{3}$ 现在， $ 3\sqrt{3}+2\sqrt {27}+\frac{7}{\sqrt{3}}$ =$3\sqrt{3}+6\sqrt{3}+( \frac{7\sqrt{3}}{3})$ =$9\sqrt{3}+( \frac{7\sqrt{3}}{3})$ =$\frac{( 27\sqrt{3}+7\sqrt{3})}{3}$ =$\frac{34\sqrt{3}}{3}$ 因此，$3\sqrt{3}+2\sqrt{27}+\frac {7}{\sqrt{3}}=\frac {34\sqrt{3}}{3}$。
已知： $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=x, \ \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}=y$。求解：求 $x^{2}+y^{2}+x y$ 的值。解：如题所示 $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=x, \ \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}=y$ ∵ $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=x$ $x=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\times \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}$ [将分子和分母都乘以 √3+√2] =$\frac{( \sqrt{3}+\sqrt{2})^2}{( ( \sqrt{3})^2-( \sqrt{2})^2)}$=$\frac{( \sqrt{3})^2+2\sqrt{3}\sqrt{2}+( \sqrt{2})^2}{3-2}$=$\frac{3+2\sqrt{6}+2}{1}$=$5+2\sqrt{6}$ => $x^2=( 5+2\sqrt{6})^2$ => $x^2=5^2+2\times5\times2\sqrt{6}+( 2\sqrt{6})^2$ => $x^2=25+20\sqrt{6}+24$ => $x^2=49+20\sqrt{6}$ 同样地，$y^2=49-20\sqrt{6}$ 因此，$x^2+xy+y^2=49+\sqrt{6}+( \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}})( \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}})+49-\sqrt{6}$ =$98+1$ =$99$ 因此， $x^2+xy+y^2=99$。阅读更多
已知：$9^{\frac{3}{2}}-3 \times 5^{0}-( \frac{1}{81})^{-\frac{1}{2}}$。求解：解方程 $9^{\frac{3}{2}}-3 \times 5^{0}-( \frac{1}{81})^{-\frac{1}{2}}$。解：$9^{\frac{3}{2}}-3 \times 5^{0}-( \frac{1}{81})^{-\frac{1}{2}}$=$( 3^2)^{\frac{3}{2}}-3 \times 1-( \frac{1}{3^4})^{-\frac{1}{2}}$=$3^{2\times\frac{3}{2}}-3-( 3^{-4})^{-\frac{1}{2}}$=$3^3-3-3^{-4\times-\frac{1}{2}}$=$3^3-3-3^2$=$27-3-9$=$15$ 因此，$9^{\frac{3}{2}}-3 \times 5^{0}-( \frac{1}{81})^{-\frac{1}{2}}=15$。
已知：10$\frac{1}{2}$ 吨沙子要分给几个建筑商。其中一个建筑商收到总沙子的 $\frac{4}{7}$，剩下的沙子由 3 个建筑商平分。求解：计算第四个建筑商收到多少沙子，以及其他 3 个建筑商各收到多少沙子。解：第四个建筑商收到的沙子吨数为 $(\frac{4}{7}) \times$ 总沙子吨数。第四个建筑商收到的沙子量 = $(\frac{4}{7}) \times (\frac{21}{2}) = 6$ 吨。剩余沙子吨数 = 总沙子 - 给第四个建筑商的沙子 = $(\frac{21}{2}) - 6 = \frac{3}{2}$ 其他三个建筑商收到的沙子量为... 阅读更多
解：(i). $( b-7)^2$ =$b^2+7^2-2( b)( 7)$ =$b^2+49-14b$ ∵ $[(a-b)^2=a^2+b^2-2ab]$ (ii). $( xy+3z)^2$ =$( xy)^2+( 3z)^2+2( xy)( 3z)$ =$x^2y^2+9z^2+6xyz$ ∵ $[(a+b)^2=a^2+b^2+2ab]$ (iii). $( 6x-5y)^2$ =$( 6x)^2+( 5y)^2-2( 6x)( 5y)$ =$36x^2+25y^2-60xy$ ∵ $[( a-b)^2=a^2+b^2-2ab]$ (iv). $( \frac{2}{3}m+\frac{3}{2}n)^2$ =$( \frac{2}{3}m)^2+( \frac{3}{2}n)^2+2( \frac{2}{3}m)( \frac{3}{2}n)$ =$\frac{4}{9}m^2+\frac{9}{4}n^2+2mn$ ∵ $[(a+b)^2=a^2+b^2+2ab]$ (v). $(0.4p-0.5q)^2$ =$( 0.4p)^2+( 0.5q)^2-2( 0.4p)( 0.5q)$ =$0.16p^2+0.25q^2-4pq$ ∵ $[( a-b)^2=a^2+b^2-2ab]$
1. 物体移动了一段距离，但如果它回到起始点，则位移可以为零。位移是指起始点和终点之间的直线距离，或者说是两点之间的最短距离。例如，绕着圆形体育场跑一圈回到起点，尽管距离是一个正值，但位移为零。2. 已知，正方形田地的边长 = 10 米，沿着正方形田地移动所用的时间 = 40 秒，农民绕正方形行走……阅读更多
已知：一个等边三角形棱柱。求解：写出等边三角形棱柱的体积公式。解：如果我们有一个边长为 $a$，高为 $h$ 的等边三角形棱柱，则体积 $\boxed{V=\frac{\sqrt{3}}{4}a^2h}$