已知:连接点 $(-4, 0)$ 和 $(0, 6)$ 的线段被分成四等份。求解:求连接点 $(-4, 0)$ 和 $(0, 6)$ 的线段被分成四等份的点的坐标。解答:设线段 AB 的端点为 A(-4, 0) 和 B(0, 6)。设 P、Q、R 为将 AB 分成四等份的点。这意味着 AP=PQ=QR=RB。Q 是 AB 的中点,P… 阅读更多
已知:学校举办了为期四天的图书展览。第一天、第二天、第三天和最后一天售出的门票数量分别为 $1094、1812、2050$ 和 $2751$。求解:求这四天售出的门票总数。解答:已知第一天、第二天、第三天和最后一天售出的门票数量分别为 $1094、1812、2050$ 和 $2751$。这四天售出的门票总数 = $1094 + 1812 + 2050 + 2751 = 7707$。因此,这四天售出的门票总数为 7707 张。
已知:数字 $5,737,802$。求解:将给定的数字用国际数字系统表示:$5,737,802$。解答:给定数字:$5,737,802 = (5 \times 百万) + (7 \times 十万) + (3 \times 万) + (7 \times 千) + (8 \times 百) + (0 \times 十) + (2 \times 个) = (5 \times 1,000,000) + (7 \times 100,000) + (3 \times 10,000) + (7 \times 1,000) + (8 \times 100) + (0 \times 10) + (2 \times 1) = 5,000,000 + 700,000 + 30,000 + 7,000 + 800 + 0 + 2 = 5,737,802$
在代数中,未知数指的是我们不知道的数。我们称它们为代数中的变量。例如:$x、y、k、a、b$。
已知:一辆踏板车以 42,000 卢比的价格购买。它的价值以每年 8% 的速度贬值。求解:求一年后的价值。解答:已知,本金 (P) = 42,000 卢比,利率 (R) = 8%,时间 (t) = 1 年。应付金额 (A) = P(1 - R/100)^t ⇒ A = P(1 - R/100)^1 ⇒ A = 42000(1 - 8/100)^1 ⇒ A = 42000(1 - 0.08)^1 ⇒ A = 42000(0.92) ⇒ A = 38640 卢比。因此,一年后踏板车的价值为 38,640 卢比。
已知:连接点 A(3, -3) 和 B(-2, 7) 的线段被 x 轴分割。求解:求分割比例和分割点的坐标。解答:分割该线段的点位于 x 轴上。这意味着它的纵坐标为 0。设点 P(x, 0) 以 m:n 的比例分割连接点 A(3, -3) 和 B(-2, 7) 的线段。使用截距公式,我们有,(x, y) = (mx2 + nx1 / (m + n), my2 + ny1 / (m + n)) 因此,P(x, 0) = (m × (-2) + n × 3 / (m + n), m × 7 + n × (-3) / (m + n)) ⇒ (7m - 3n) / (m + n) = 0 ⇒ 7m - 3n = 0 ⇒ 7m = 3… 阅读更多
已知:点 P(x, 2) 分割连接点 A(12, 5) 和 B(4, -3) 的线段。求解:求分割比例和 x 的值。解答:使用截距公式,如果点 (x, y) 以 m:n 的比例分割连接点 (x1, y1) 和 (x2, y2) 的线段,则 (x, y) = (mx2 + nx1 / (m + n), my2 + ny1 / (m + n)) 设比例为 m:n,这意味着 P(x, 2) = (m(4) + n(12) / (m + n), m(-3) + n(5) / (m + n)) ⇒ 2 = m(-3) + n(5) / (m + n) ⇒ 2(m + n) = -3m + 5n ⇒ 2m + 2n = -3m + 5n ⇒ 2m + 3m = 5n - 2n ⇒ 5m = 3n ⇒ m / n = 3 / 5 ⇒ m:n = 3:5 现在,x = mx2 + nx1 / (m + n) ⇒ x = 3(4) + 5(12) / (3 + 5) ⇒ 8x = 12 + 60 ⇒ 8x = 72 ⇒ x = 72 / 8 = 9 所需的… 阅读更多
已知:点 P(-1, y) 分割连接点 A(-3, 10) 和 B(6, -8) 的线段。求解:求分割比例和 y 的值。解答:使用截距公式,如果点 (x, y) 以 m:n 的比例分割连接点 (x1, y1) 和 (x2, y2) 的线段,则 (x, y) = (mx2 + nx1 / (m + n), my2 + ny1 / (m + n)) 此处,x1 = -3, y1 = 10, x2 = 6, y2 = -8 设比例为 m:n,这意味着 P(-1, y) = (m(6) + n(-3) / (m + n), m(-8) + n(10) / (m + n)) 因此,将两边的坐标相等,我们得到,(6m - 3n) / (m + n) = -1 ⇒ 6m - 3n = -1(m + n) ⇒ 6m - 3n = -m - n) ⇒ 6m + m = 3n - n ⇒ 7m = 2n ⇒ m / n = 2 / 7 ⇒ m:n = 2:7 现在,y = -8m + 10n / (m + n) ⇒ y = -8(2) + 10(7) / … 阅读更多
已知:AB 是圆的直径,圆心为 $(2, -3)$,B 点坐标为 $(1, 4)$。求解:求 A 点的坐标。解:设圆心为 O$(2, -3)$,A 点坐标为 $(x, y)$。AB 是以 O 为圆心的圆的直径。这意味着 O 是 AB 的中点。我们知道,两点 $(x_1, y_1)$ 和 $(x_2, y_2)$ 的中点坐标为 $(x, y) = (\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$。利用中点公式,$(2, -3) = (\frac{x+1}{2}, \frac{y+4}{2})$。将两边坐标相等,得到……阅读更多
已知:点 $(-2, -1), (1, 0), (x, 3)$ 和 $(1, y)$ 构成一个平行四边形。求解:求 x 和 y 的值。解:设平行四边形的顶点为 A$(-2, -1)$,B$(1, 0)$,C$(x, 3)$ 和 D$(1, y)$,且对角线 AC 和 BD 相交于点 O。O 是 AC 的中点。这意味着,利用中点公式,O 的坐标为 $(\frac{-2+x}{2}, \frac{-1+3}{2}) = (\frac{-2+x}{2}, 1)$。O 也是 BD 的中点。这意味着,O 的坐标为 $(\frac{1+1}{2}, \frac{0+y}{2}) = (1, \frac{y}{2})$。因此,$1 = \frac{-2+x}{2}$ 且……阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
 "\
"\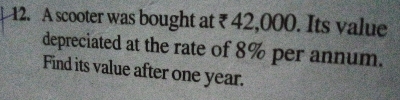 "\
"\