已知:矩形 ABCD 的尺寸为 21 cm × 14 cm。半圆的直径 = BC。要求:求阴影部分的面积和周长。解:∵ BC 是所画圆的直径 = BC = 14 cm ∴ 半圆的半径,r = 14/2 = 7 cm阴影区域的面积 = 矩形的面积 - 半圆的面积= 21 × 14 - πr²/2= 294 - 77= 217 cm²阴影区域的周长 = AB + AD + CD + 弧 BC 的长度= 21 + 14 + 21 + πr (∵ 弧长 = 以 BC 为直径的半圆的周长)= 56 + 22/7 × 7= 56 + 22= 78 cm因此,阴影部分的面积… 阅读更多
已知:飞机的高度 = 300 m,飞机上观察到河两岸相对方向两点的俯角分别为 45° 和 30°。要求:求河流的宽度。解:已知飞机的高度为 300 m。AB = 300 m 且 XY || PQ。两点 P 和 Q 的俯角分别为 30° 和 45°。∠XAP = 30° 且 ∠YAQ = 45°∠XAP = ∠APB = 30° 且 ∠YAQ = ∠AQB = 45°在 △APB 中,tan 30° = AB/PB1/√3 = AB/PB PB = AB√3 = 300√3 m在 △BAQ 中,tan 45° = AB/BQ1 = 300/BQ BQ = 300 m河流的宽度 PQ = PB + BQ = 300 + 300√3 = 300(1 + √3) 米。 阅读更多
已知:边 BC = 7 cm,∠B = 45°,∠A = 105°。要求:作一个三角形 ABC,其中 BC = 7 cm,∠B = 45°,∠A = 105°,然后作另一个三角形,其边长是 ABC 对应边长的 3/4 倍。解:这里 BC = 7 cm,∠B = 45°,∠A = 105°画出 BC = 7cm借助直尺用量角器测量 ∠45°从点 B 开始并画出一条射线 BX。从点上用量角器标记 30°并画出一条射线 CY。现在 BX 和 BY 相交于… 阅读更多
已知:方程 1/(x+1) + 3/(5x+1) = 5/(x+4),x≠1,-1/5,-4要求:通过解方程求 x 的值。解:给定方程:1/(x+1) + 3/(5x+1) = 5/(x+4)⇒ (5x+1+3x+3)/((x+1)(5x+1)) = 5/(x+4)⇒ (8x+4)/(5x²+5x+x+1) = 5/(x+4)⇒ (8x+4)(x+4) = 5(5x²+6x+1)⇒ 8x²+32x+4x+16 = 25x²+30x+5⇒ 25x²+30x+5 - 8x² - 32x - 4x - 16 = 0⇒ 17x² - 6x - 11 = 0⇒ 17x² - 17x + 11x - 11 = 0⇒ 17x(x-1) + 11(x-1) = 0⇒ (17x+11)(x-1) = 0如果 17x+11=0⇒ x=-11/17如果 x-1=0⇒ x=1∴ x=-11/17,1。 阅读更多
已知:两个水龙头一起注满水箱所需时间 = 3 1/13 小时。要求:求每个水龙头注满水箱所需时间。解:两个水龙头一起注满水箱需要 3 1/13 小时 = 40/13 小时假设水龙头分别为 A、B,水龙头 A 单独注满水箱需要 x 小时水龙头 B 注满水箱需要 (x+3) 小时水龙头 A (1 小时内) 注满的水箱部分 = 1/x水龙头 B (1 小时内) 注满的水箱部分 = 1/(x+3)水龙头 A 和 B (1 小时内) 注满的水箱部分 = 1/x + 1/(x+3) = 13/401/x +… 阅读更多
已知:两个等差数列前 n 项和的比值为 (7n + 1):(4n + 27)要求:求这两个等差数列第 9 项的比值。解:给定两个等差数列,每个数列有 n 项对于第一个等差数列,假设首项为 a₁,公差为 d₁则前 n 项和,S(第一个等差数列) = n/2(2a₁ + (n-1)d₁)类似地,第二个等差数列的首项为 a₂,公差为 d₂。前 n 项和,S(第二个等差数列) = n/2(2a₂ + (n-1)d₂)如给定,S(第一个等差数列)/S(第二个等差数列) = (7n+1)/(4n+27)⇒ n/2(2a₁ + (n-1)d₁)/n/2(2a₂ + (n-1)d₂) = (7n+1)/(4n+27)⇒ (a₁ + (n-1)/2d₂)/(a₂ + (… 阅读更多
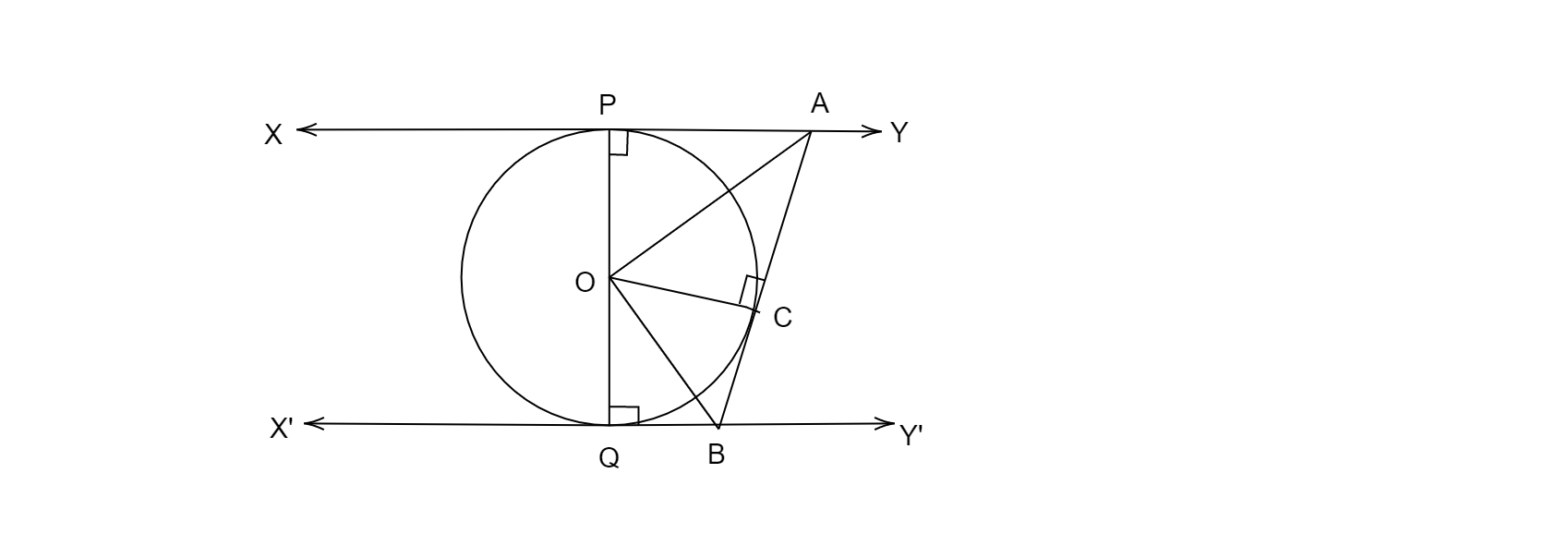
已知:以 O 为圆心的圆,两条平行切线 XY 和 X'Y' 分别与圆相切,另一条切线在 C 点与圆相切,分别与 l 和 m 相交于 A 和 B。要求:证明 ∠AOB = 90°。解:XY 和 X'Y' 是两个平行于圆心 O 的圆的平行切线,分别与圆相切于 P 和 Q。AB 是在 C 点的切线,它与 XY 相交于 A,与 X'Y' 相交于 B。步骤如下:连接 OC。在 △OAP 和 △OAC 中,OP = OC (半径…) 阅读更多
**已知:**一个长方体,其尺寸为 $4.4\ m\times \ 2.6m\times 1.0\ m$。管道的半径 $=30\ cm$,内壁厚度 $=5\ cm$。**求:**求管道的长度。**解:**长方体的体积 $=4.4\ m\times \ 2.6m\times 1.0\ m.=11.44\ m^{2}$假设管道的长度 $=l\ cm=\frac{l}{100} \ m$内半径 $=\ 30\ cm=\frac{30}{100}\ m$外半径 $=35\ cm=\frac{35}{100}\ m$圆柱形管道的体积$=\pi \left( r^{2}_{1} -r^{2}_{2}\right) l$$=\pi \times \frac{1}{100\times 100}\left( 35^{2} -30^{2}\right) l\ m^{3}$长方体的体积 = 圆柱形管道的体积$11.44=\frac{\pi l}{100\times 100\times 100}\left( 35^{2} -30^{2}\right)$$\Rightarrow l=\frac{11.44\times 100\times 100\times 100}{\pi \times 65\times 5}$$\Rightarrow l=10.205\times 10^{4} \ m^{3}$$\Rightarrow l=102.05\ km$因此,管道的长度... 阅读更多
**已知:**水渠宽度 $=\ 5.4\ mt$,深度$=1.8\ mt$,水流速度 $=25\ km/hr$,所需积水 $=10\ cm$。**求:**求 40 分钟内可以灌溉的面积。**解:**已知水渠宽度$=\ 5.4\ mt$深度$=\ 1.8\ mt$水流速度 $= 25\ km/hr$所需灌溉水深$=10\ cm=10\times 10^{-2}$40 分钟内水流动的距离$=\frac{25\times 40}{60}\ km$$=\frac{50}{3} \ km$流经管道的水的体积$=\frac{50}{3} \times 5.4\times 1.8\times 1000$$=162\times 10^{3} \ m^{3}$用 10 cm 深的水灌溉的面积 $=\frac{162\times 10^{3}}{10\times 10^{-2}}$$=162\times 10^{4} \ m^{2}$用 10 cm 深的水灌溉的面积为 $162\times 10^{4} \ m^{2}$
**已知:**圆台的斜高为 4 厘米,其圆形底面的周长分别为 18 厘米和 6 厘米。**求:**求圆台的侧面积。**解:**$l=4\ cm$一个圆形底面的周长 $=18\ cm$$\Rightarrow 2\pi r_{1}=18$$\Rightarrow \pi \times r_{1}=\frac{18}{2}=9$ ............. $( 1)$另一个圆形底面的周长 $=6\ cm$$\Rightarrow 2\pi r_{2}=6$$\Rightarrow \pi r_{2}=\frac{6}{2}=3$ ............. $( 2)$将 $( 1)$ 和 $( 2)$ 相加$\pi r_{1}+\pi r_{2}=9+3=12$侧面积$=\pi(r_{1}+r_{2})l$$=(9+3)\times 4$$=48\ cm^2$因此,圆台的侧面积为 $48\ cm^{2}$.

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP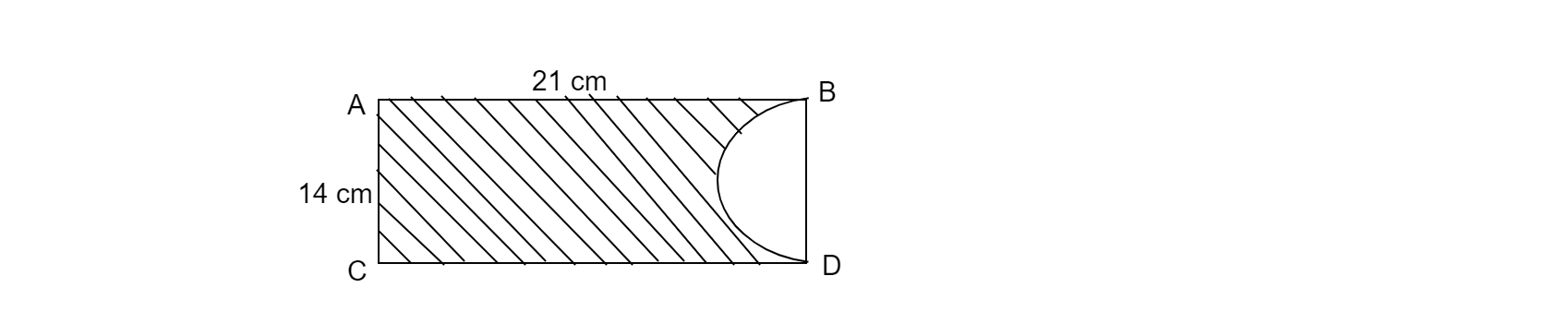 "\
"\
 "\
"\