
人工神经网络 - 基本概念
神经网络是并行计算设备,它本质上是试图创建大脑的计算机模型。其主要目标是开发一个系统,使其能够比传统系统更快地执行各种计算任务。这些任务包括模式识别和分类、逼近、优化和数据聚类。
什么是人工神经网络?
人工神经网络(ANN)是一种高效的计算系统,其核心主题借鉴了生物神经网络的类比。ANN也被称为“人工神经系统”、“并行分布式处理系统”或“连接主义系统”。ANN 获取大量相互连接的单元,这些单元以某种模式连接以允许单元之间进行通信。这些单元,也称为节点或神经元,是并行运行的简单处理器。
每个神经元都通过连接链路与其他神经元连接。每个连接链路都与一个权重相关联,该权重包含有关输入信号的信息。这是神经元解决特定问题最有用的信息,因为权重通常会激发或抑制正在传递的信号。每个神经元都有一个内部状态,称为激活信号。输出信号是在组合输入信号和激活规则后产生的,可以发送到其他单元。
ANN 的简史
ANN 的历史可以分为以下三个时期:
1940 年代至 1960 年代的 ANN
这个时期的几个关键发展如下:
1943 - 人们认为,神经网络的概念始于生理学家沃伦·麦卡洛克和数学家沃尔特·皮茨的工作,他们在 1943 年使用电路对一个简单的神经网络进行了建模,以描述大脑中的神经元如何工作。
1949 - 唐纳德·赫布的著作《行为的组织》提出,一个神经元对另一个神经元的重复激活会增加它们每次使用时的强度。
1956 - 泰勒引入了联想记忆网络。
1958 - 罗森布拉特发明了一种用于麦卡洛克和皮茨神经元模型的学习方法,名为感知器。
1960 - 伯纳德·维德罗和马西安·霍夫开发了名为“ADALINE”和“MADALINE”的模型。
1960 年代至 1980 年代的 ANN
这个时期的几个关键发展如下:
1961 - 罗森布拉特进行了一次不成功的尝试,但提出了用于多层网络的“反向传播”方案。
1964 - 泰勒构建了一个赢者通吃的电路,输出单元之间存在抑制。
1969 - 明斯基和帕普特发明了多层感知器 (MLP)。
1971 - 科霍宁开发了联想记忆。
1976 - 斯蒂芬·格罗斯伯格和盖尔·卡彭特开发了自适应谐振理论。
1980 年代至今的 ANN
这个时期的几个关键发展如下:
1982 - 主要发展是霍普菲尔德的能量方法。
1985 - 阿克利、欣顿和塞诺夫斯基开发了玻尔兹曼机。
1986 - 鲁梅哈特、欣顿和威廉姆斯引入了广义 delta 规则。
1988 - 科斯科开发了二元联想记忆 (BAM),并提出了 ANN 中模糊逻辑的概念。
历史回顾表明,该领域取得了显著进展。基于神经网络的芯片正在出现,并正在开发针对复杂问题的应用。毫无疑问,今天是神经网络技术的一个过渡时期。
生物神经元
神经细胞(神经元)是一种特殊的生物细胞,负责处理信息。据估计,神经元的数量巨大,大约为 1011 个,并且具有大量相互连接,大约为 1015 个。
示意图
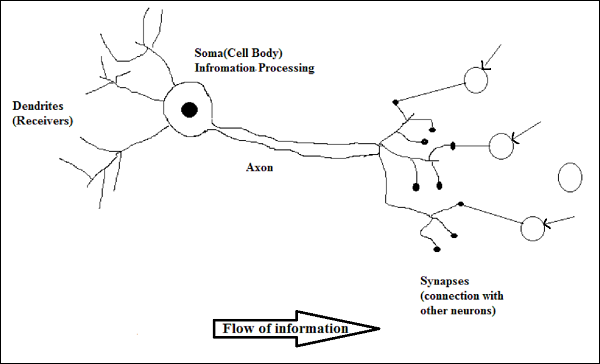
生物神经元的工作原理
如上图所示,一个典型的神经元由以下四个部分组成,我们可以用它们来解释其工作原理:
树突 - 它们是树状分支,负责接收与其连接的其他神经元的信息。换句话说,我们可以说它们像神经元的耳朵。
胞体 - 它是神经元的细胞体,负责处理从树突接收到的信息。
轴突 - 它就像一条电缆,神经元通过它发送信息。
突触 - 它是轴突和其他神经元树突之间的连接。
ANN 与 BNN
在查看人工神经网络 (ANN) 和生物神经网络 (BNN) 之间的区别之前,让我们先看看这两个术语之间的相似之处。
| 生物神经网络 (BNN) | 人工神经网络 (ANN) |
|---|---|
| 胞体 | 节点 |
| 树突 | 输入 |
| 突触 | 权重或互连 |
| 轴突 | 输出 |
下表显示了基于某些提到的标准对 ANN 和 BNN 的比较。
| 标准 | BNN | ANN |
|---|---|---|
| 处理 | 大规模并行,速度慢但优于 ANN | 大规模并行,速度快但劣于 BNN |
| 大小 | 1011 个神经元和 1015 个互连 | 102 到 104 个节点(主要取决于应用程序类型和网络设计者) |
| 学习 | 它们可以容忍模糊性 | 需要非常精确、结构化和格式化的数据才能容忍模糊性 |
| 容错性 | 即使部分损坏,性能也会下降 | 它能够提供强大的性能,因此具有容错的潜力 |
| 存储容量 | 将信息存储在突触中 | 将信息存储在连续的内存位置中 |
人工神经网络模型
下图表示 ANN 的通用模型及其处理过程。
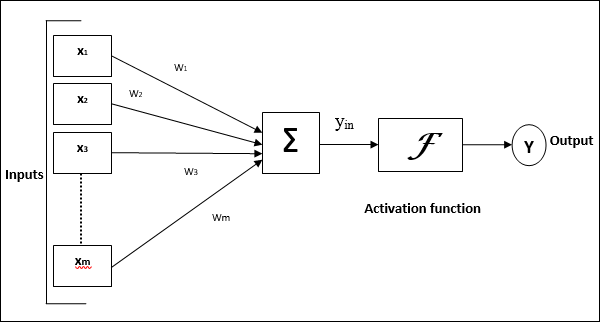
对于上述人工神经网络的通用模型,净输入可以计算如下:
$$y_{in}\:=\:x_{1}.w_{1}\:+\:x_{2}.w_{2}\:+\:x_{3}.w_{3}\:\dotso\: x_{m}.w_{m}$$
即,净输入 $y_{in}\:=\:\sum_i^m\:x_{i}.w_{i}$
可以通过对净输入应用激活函数来计算输出。
$$Y\:=\:F(y_{in}) $$
输出 = 函数(计算的净输入)