
使用Hopfield网络进行优化
优化是指使设计、情况、资源和系统等尽可能有效地发挥作用。利用成本函数和能量函数之间的相似性,我们可以使用高度互连的神经元来解决优化问题。这种神经网络就是Hopfield网络,它由一层包含一个或多个完全互连的递归神经元组成。这可以用于优化。
使用Hopfield网络进行优化时需要注意的几点:
网络的能量函数必须最小。
它会找到令人满意的解,而不是从存储的模式中选择一个。
Hopfield网络找到的解的质量很大程度上取决于网络的初始状态。
旅行商问题
寻找旅行商旅行的最短路线是可以通过使用Hopfield神经网络进行优化的计算问题之一。
TSP的基本概念
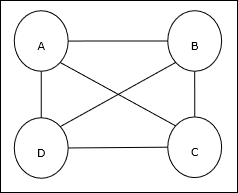
旅行商问题 (TSP) 是一个经典的优化问题,其中一名销售人员必须前往**n**个相互连接的城市,同时使成本和旅行距离最小化。例如,销售人员必须前往一组4个城市A、B、C、D,目标是找到最短的环形路线A-B-C-D,以最小化成本,这还包括从最后一个城市D到第一个城市A的旅行成本。
矩阵表示
实际上,每个n城市TSP的路线都可以表示为一个**n × n**矩阵,其第**i**行描述第**i**个城市的位置。对于4个城市A、B、C、D,此矩阵**M**可以表示如下:
$$M = \begin{bmatrix}A: & 1 & 0 & 0 & 0 \\B: & 0 & 1 & 0 & 0 \\C: & 0 & 0 & 1 & 0 \\D: & 0 & 0 & 0 & 1 \end{bmatrix}$$
Hopfield网络的解决方案
在考虑Hopfield网络对TSP的解决方案时,网络中的每个节点对应于矩阵中的一个元素。
能量函数计算
为了获得最佳解,能量函数必须最小。根据以下约束,我们可以计算能量函数如下:
约束I
我们将根据其计算能量函数的第一个约束是,矩阵**M**的每一行中必须有一个元素等于1,而每一行中的其他元素必须等于**0**,因为每个城市在TSP路线中只能出现一个位置。此约束可以用数学方式写成如下:
$$\displaystyle\sum\limits_{j=1}^n M_{x,j}\:=\:1\:for \: x\:\in \:\lbrace1,...,n\rbrace$$
现在,基于上述约束,要最小化的能量函数将包含一个与以下成比例的项:
$$\displaystyle\sum\limits_{x=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{j=1}^n M_{x,j}\end{array}\right)^2$$
约束II
众所周知,在TSP中,一个城市可以在路线中的任何位置出现,因此在矩阵**M**的每一列中,必须有一个元素等于1,而其他元素必须等于0。此约束可以用数学方式写成如下:
$$\displaystyle\sum\limits_{x=1}^n M_{x,j}\:=\:1\:for \: j\:\in \:\lbrace1,...,n\rbrace$$
现在,基于上述约束,要最小化的能量函数将包含一个与以下成比例的项:
$$\displaystyle\sum\limits_{j=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x=1}^n M_{x,j}\end{array}\right)^2$$
成本函数计算
假设一个用**C**表示的( **n × n** )方阵表示**n**个城市(其中**n > 0**)的TSP成本矩阵。在计算成本函数时,以下是一些参数:
**Cx, y** - 成本矩阵的元素表示从城市**x**到**y**的旅行成本。
元素A和B的邻接性可以用以下关系表示:
$$M_{x,i}\:=\:1\:\: and\:\: M_{y,i\pm 1}\:=\:1$$
众所周知,在矩阵中,每个节点的输出值可以是0或1,因此对于每对城市A、B,我们可以向能量函数添加以下项:
$$\displaystyle\sum\limits_{i=1}^n C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})$$
基于上述成本函数和约束值,最终能量函数**E**可以表示为:
$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{x}\displaystyle\sum\limits_{y\neq x}C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})\:+$$
$$\:\begin{bmatrix}\gamma_{1} \displaystyle\sum\limits_{x} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{i} M_{x,i}\end{array}\right)^2\:+\: \gamma_{2} \displaystyle\sum\limits_{i} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x} M_{x,i}\end{array}\right)^2 \end{bmatrix}$$
这里,**γ1** 和 **γ2** 是两个加权常数。