
人工神经网络 - 学习与适应
如前所述,ANN完全受到生物神经系统,即人脑工作方式的启发。人脑最令人印象深刻的特点是学习,因此ANN也获得了同样的特性。
什么是ANN中的学习?
基本上,学习意味着根据环境的变化而进行自身调整和适应。ANN是一个复杂系统,更准确地说,它是一个复杂的自适应系统,它可以根据通过它的信息改变其内部结构。
为什么学习很重要?
作为一个复杂的自适应系统,ANN中的学习意味着处理单元能够由于环境的变化而改变其输入/输出行为。由于构建特定网络时激活函数和输入/输出向量是固定的,因此ANN中学习的重要性就提高了。现在要改变输入/输出行为,我们需要调整权重。
分类
它可以定义为通过查找相同类别样本之间的共同特征来学习将样本数据区分到不同类别中的过程。例如,为了执行ANN的训练,我们有一些具有独特特征的训练样本,为了执行其测试,我们有一些具有其他独特特征的测试样本。分类是监督学习的一个例子。
神经网络学习规则
我们知道,在ANN学习过程中,要改变输入/输出行为,我们需要调整权重。因此,需要一种可以修改权重的方法。这些方法称为学习规则,它们只是算法或方程。以下是神经网络的一些学习规则:
Hebb学习规则
这条规则是最古老和最简单的规则之一,由唐纳德·赫布 (Donald Hebb) 在他1949年的著作《行为的组织》(The Organization of Behavior) 中提出。它是一种前馈无监督学习。
基本概念 - 这条规则基于赫布提出的一个假设,他写道:
“当细胞A的轴突足够接近于激发细胞B,并且反复或持续地参与激发它时,在一个或两个细胞中都会发生某种生长过程或代谢变化,从而提高了A作为激发B的细胞之一的效率。”
从上述假设中,我们可以得出结论,如果两个神经元同时放电,则它们之间的连接可能会增强;如果它们在不同时间放电,则可能会减弱。
数学公式 - 根据Hebb学习规则,以下是每次步长增加连接权重的公式。
$$ \Delta w_{ji}(t) = \alpha x_{i}(t) \cdot y_{j}(t) $$
这里,$ \Delta w_{ji}(t) $ = 在时间步长t时连接权重增加的增量
$ \alpha $ = 正的常数学习率
$ x_{i}(t) $ = 在时间步长t时来自突触前神经元的输入值
$ y_{i}(t) $ = 在相同时间步长t时突触前神经元的输出
感知器学习规则
这条规则是由罗森布拉特 (Rosenblatt) 提出的单层前馈网络的误差校正监督学习算法,具有线性激活函数。
基本概念 - 由于其监督性质,为了计算误差,需要将期望/目标输出与实际输出进行比较。如果发现有任何差异,则必须对连接权重进行更改。
数学公式 - 为了解释其数学公式,假设我们有“n”个有限的输入向量x(n),以及其期望/目标输出向量t(n),其中n = 1到N。
现在可以计算输出'y',如前面根据净输入所解释的那样,并应用于该净输入的激活函数可以表示如下:
$$ y = f(y_{in}) = \begin{cases} 1, & y_{in} > \theta \\ 0, & y_{in} \le \theta \end{cases} $$
其中θ是阈值。
权重的更新可以在以下两种情况下进行:
情况一 - 当t ≠ y时,则
$$ w(new) = w(old) + tx $$
情况二 - 当t = y时,则
权重不变
Delta学习规则 (Widrow-Hoff规则)
它是由伯纳德·维德罗 (Bernard Widrow) 和马西恩·霍夫 (Marcian Hoff) 提出的,也称为最小均方 (LMS) 方法,用于最小化所有训练模式的误差。它是一种具有连续激活函数的监督学习算法。
基本概念 - 这条规则的基础是梯度下降法,它会无限持续下去。Delta规则更新突触权重,以最小化输出单元的净输入和目标值之间的差异。
数学公式 - 为了更新突触权重,Delta规则由下式给出
$$ \Delta w_{i} = \alpha \cdot x_{i} \cdot e_{j} $$
这里 $ \Delta w_{i} $ = 第i个模式的权重变化;
$ \alpha $ = 正的常数学习率;
$ x_{i} $ = 来自突触前神经元的输入值;
$ e_{j} $ = $ (t - y_{in}) $,期望/目标输出与实际输出 $ y_{in} $ 之间的差值
上述Delta规则仅适用于单个输出单元。
权重的更新可以在以下两种情况下进行:
情况一 - 当t ≠ y时,则
$$ w(new) = w(old) + \Delta w $$
情况二 - 当t = y时,则
权重不变
竞争学习规则 (赢者通吃)
它关注的是无监督训练,其中输出节点相互竞争以表示输入模式。要理解这个学习规则,我们必须理解如下所示的竞争网络:
竞争网络的基本概念 - 这个网络就像一个单层前馈网络,输出之间有反馈连接。输出之间的连接是抑制类型的,用虚线表示,这意味着竞争者永远不会相互支持。
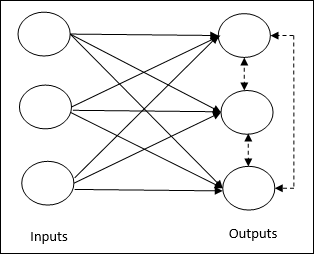
竞争学习规则的基本概念 - 如前所述,输出节点之间会存在竞争。因此,主要概念是,在训练过程中,对给定输入模式具有最高激活的输出单元将被宣布为获胜者。这条规则也称为赢者通吃,因为只有获胜神经元会更新,其余神经元保持不变。
数学公式 - 以下是该学习规则数学公式的三个重要因素:
获胜条件 - 如果神经元 $ y_{k} $ 想获胜,则会有以下条件:
$$ y_{k} = \begin{cases} 1 & \text{if } v_{k} > v_{j} \text{ for all } j, j \ne k \\ 0 & \text{otherwise} \end{cases} $$
这意味着如果任何神经元,例如 $ y_{k} $,想要获胜,则其感应局部场(求和单元的输出),例如 $ v_{k} $,必须是网络中所有其他神经元中最大的。
权重总和条件 - 竞争学习规则的另一个约束是,特定输出神经元的权重总和将为1。例如,如果我们考虑神经元k,则:
$$ \sum_{j} w_{kj} = 1 \quad \text{for all } k $$
获胜者的权重变化 - 如果神经元对输入模式没有响应,则该神经元不会发生学习。但是,如果特定神经元获胜,则相应权重将调整如下:
$$ \Delta w_{kj} = \begin{cases} -\alpha(x_{j} - w_{kj}), & \text{if neuron } k \text{ wins} \\ 0, & \text{if neuron } k \text{ loses} \end{cases} $$
这里 $ \alpha $ 是学习率。
这清楚地表明,我们通过调整其权重来偏向获胜神经元,如果存在神经元损失,则我们不必费心重新调整其权重。
Outstar学习规则
这条规则由格罗斯伯格 (Grossberg) 提出,它关注的是监督学习,因为期望输出是已知的。它也称为格罗斯伯格学习。
基本概念 - 这条规则应用于排列在一层中的神经元。它专门设计用于产生p个神经元层的期望输出d。
数学公式 - 此规则中的权重调整计算如下:
$$ \Delta w_{j} = \alpha (d - w_{j}) $$
这里d是期望神经元输出,$ \alpha $ 是学习率。