Kohonen 自组织特征映射

假设我们有一些任意维度的模式，但我们需要将它们转换为一维或二维。那么特征映射的过程对于将宽模式空间转换为典型的特征空间非常有用。现在，问题出现了，为什么我们需要自组织特征映射？原因是，除了能够将任意维度转换为一维或二维外，它还必须具有保留邻域拓扑的能力。

Kohonen SOM 中的邻域拓扑

可以有多种拓扑结构，但以下两种拓扑结构使用得最多：

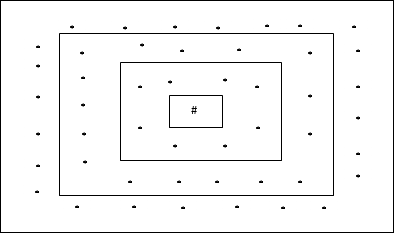
矩形网格拓扑

这种拓扑结构在距离 2 的网格中有 24 个节点，距离 1 的网格中有 16 个节点，距离 0 的网格中有 8 个节点，这意味着每个矩形网格之间的差异是 8 个节点。获胜单元用 # 表示。

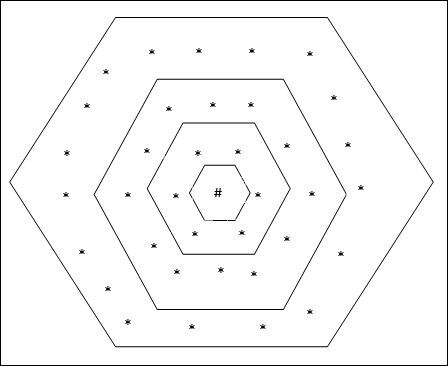
六边形网格拓扑

这种拓扑结构在距离 2 的网格中有 18 个节点，距离 1 的网格中有 12 个节点，距离 0 的网格中有 6 个节点，这意味着每个矩形网格之间的差异是 6 个节点。获胜单元用 # 表示。

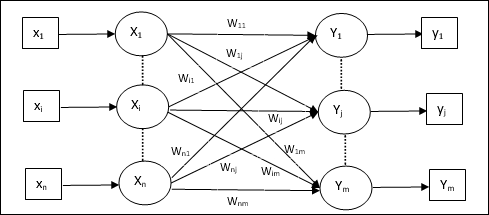
架构

KSOM 的架构类似于竞争网络。借助前面讨论的邻域方案，可以在网络的扩展区域进行训练。

训练算法

步骤 1 - 初始化权重、学习率 α 和邻域拓扑方案。

步骤 2 - 当停止条件不为真时，继续步骤 3-9。

步骤 3 - 对于每个输入向量 x，继续步骤 4-6。

步骤 4 - 计算 j = 1 到 m 的欧几里得距离平方

$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n \displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$

步骤 5 - 获取获胜单元 J，其中 D(j) 最小。

步骤 6 - 通过以下关系计算获胜单元的新权重：

$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha[x_{i}\:-\:w_{ij}(old)]$$

步骤 7 - 通过以下关系更新学习率 α：

$$\alpha(t\:+\:1)\:=\:0.5\alpha t$$

步骤 8 - 减小拓扑方案的半径。

步骤 9 - 检查网络的停止条件。