
无监督神经网络
顾名思义,这种类型的学习是在没有老师监督的情况下进行的。这个学习过程是独立的。在无监督学习下训练ANN期间,将相似类型的输入向量组合起来形成簇。当应用新的输入模式时,神经网络会给出指示输入模式所属类别的输出响应。在这种情况下,不会有来自环境的反馈来告知期望的输出是什么以及它是否正确。因此,在这种类型的学习中,网络本身必须从输入数据中发现模式、特征以及输入数据与输出之间的关系。
赢家通吃网络
这类网络基于竞争学习规则,并将使用一种策略,即选择具有最大总输入的神经元作为赢家。输出神经元之间的连接显示了它们之间的竞争,其中一个将为“开”,这意味着它将是赢家,而其他将为“关”。
以下是基于此简单概念使用无监督学习的一些网络。
汉明网络
在大多数使用无监督学习的神经网络中,计算距离和进行比较是必不可少的。这种网络是汉明网络,对于每个给定的输入向量,它将被聚类到不同的组中。以下是汉明网络的一些重要特征:
Lippmann于1987年开始研究汉明网络。
它是一个单层网络。
输入可以是二进制{0, 1}或双极性{-1, 1}。
网络的权重由示例向量计算。
它是一个固定权重网络,这意味着即使在训练期间权重也会保持不变。
Max网络
这也是一个固定权重网络,用作选择具有最高输入的节点的子网。所有节点都是完全互连的,并且在所有这些加权互连中都存在对称权重。
架构
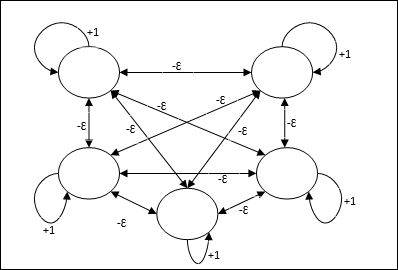
它使用迭代过程的机制,每个节点都通过连接从所有其他节点接收抑制性输入。值最大的单个节点将处于活动状态或获胜状态,而所有其他节点的激活都将处于非活动状态。Max网络使用恒等激活函数,其公式为:$$f(x)\:=\:\begin{cases}x & if\:x > 0\\0 & if\:x \leq 0\end{cases}$$
该网络的任务通过+1的自激权重和互抑制幅度来完成,该幅度设置为[0 < ɛ < $\frac{1}{m}$],其中“m”是节点的总数。
ANN中的竞争学习
它关注无监督训练,其中输出节点试图相互竞争以表示输入模式。要理解这个学习规则,我们将不得不理解如下解释的竞争网络:
竞争网络的基本概念
这个网络就像一个单层前馈网络,在输出之间具有反馈连接。输出之间的连接是抑制类型的,用虚线表示,这意味着竞争者永远不会支持自己。
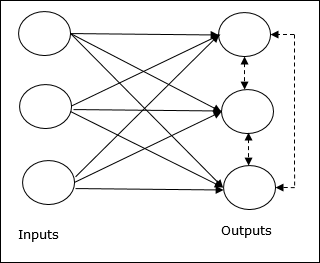
竞争学习规则的基本概念
如前所述,输出节点之间会存在竞争,因此主要概念是:在训练期间,对给定输入模式具有最高激活的输出单元将被宣布为赢家。此规则也称为赢家通吃,因为只有获胜神经元会更新,其余神经元保持不变。
数学公式
以下是此学习规则数学公式的三个重要因素:
成为赢家的条件
假设如果神经元yk想要获胜,则会有以下条件:
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k} > v_{j}\:for\:all\:\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
这意味着如果任何神经元(例如,yk)想要获胜,则其诱导局部场(求和单元的输出),例如vk,必须是网络中所有其他神经元中最大的。
权重总和的条件
对竞争学习规则的另一个约束是,对特定输出神经元的权重总和将为1。例如,如果我们考虑神经元k,则:
$$\displaystyle\sum\limits_{k} w_{kj}\:=\:1\:\:\:\:for\:all\:\:k$$
赢家的权重变化
如果神经元对输入模式没有响应,则该神经元不会发生学习。但是,如果特定神经元获胜,则相应权重将如下调整:
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0 & if\:neuron\:k\:losses\end{cases}$$
这里$\alpha$是学习率。
这清楚地表明我们通过调整其权重来偏袒获胜神经元,如果神经元输了,则我们无需费心重新调整其权重。
K均值聚类算法
K均值是最流行的聚类算法之一,其中我们使用分区过程的概念。我们从初始分区开始,反复将模式从一个聚类移动到另一个聚类,直到得到令人满意的结果。
算法
步骤1 - 选择k个点作为初始质心。初始化k个原型(w1,…,wk),例如,我们可以通过随机选择的输入向量来识别它们:
$$W_{j}\:=\:i_{p},\:\:\: where\:j\:\in \lbrace1,....,k\rbrace\:and\:p\:\in \lbrace1,....,n\rbrace$$
每个聚类Cj都与原型wj相关联。
步骤2 - 重复步骤3-5,直到E不再减小,或聚类成员资格不再改变。
步骤3 - 对于每个输入向量ip,其中p ∈ {1,…,n},将ip放入具有最近原型的聚类Cj*中,该原型具有以下关系:
$$|i_{p}\:-\:w_{j*}|\:\leq\:|i_{p}\:-\:w_{j}|,\:j\:\in \lbrace1,....,k\rbrace$$
步骤4 - 对于每个聚类Cj,其中j ∈ { 1,…,k},更新原型wj为当前在Cj中的所有样本的质心,以便:
$$w_{j}\:=\:\sum_{i_{p}\in C_{j}}\frac{i_{p}}{|C_{j}|}$$
步骤5 - 计算总量化误差如下:
$$E\:=\:\sum_{j=1}^k\sum_{i_{p}\in w_{j}}|i_{p}\:-\:w_{j}|^2$$
神经认知机
它是一个多层前馈网络,由Fukushima在20世纪80年代开发。该模型基于监督学习,用于视觉模式识别,主要是手写字符。它基本上是Cognitron网络的扩展,Cognitron网络也是由Fukushima在1975年开发的。
架构
它是一个分层网络,包含许多层,并且在这些层中存在局部连接模式。
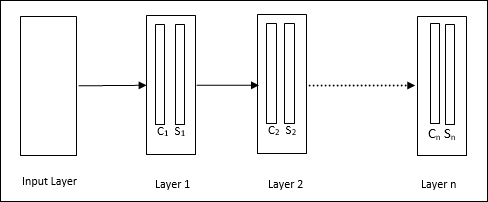
正如我们在上图中看到的,神经认知机被划分为不同的连接层,每一层都有两个单元。这些单元的解释如下:
S单元 - 它被称为简单单元,经过训练可以响应特定模式或一组模式。
C单元 - 它被称为复杂单元,它组合来自S单元的输出,同时减少每个阵列中的单元数量。换句话说,C单元会置换S单元的结果。
训练算法
神经认知机的训练被发现是逐层进行的。从输入层到第一层的权重被训练并冻结。然后,训练从第一层到第二层的权重,依此类推。S单元和C单元之间的内部计算取决于来自先前层的权重。因此,我们可以说训练算法取决于S单元和C单元的计算。
S单元中的计算
S单元拥有从前一层接收的兴奋性信号,并拥有在同一层内获得的抑制性信号。
$$\theta=\:\sqrt{\sum\sum t_{i} c_{i}^2}$$
这里,ti是固定权重,ci是来自C单元的输出。
S单元的缩放输入可以计算如下:
$$x\:=\:\frac{1\:+\:e}{1\:+\:vw_{0}}\:-\:1$$
这里,$e\:=\:\sum_i c_{i}w_{i}$
wi是从C单元到S单元的可调权重。
w0是输入和S单元之间可调的权重。
v是来自C单元的兴奋性输入。
输出信号的激活为:
$$s\:=\:\begin{cases}x, & if\:x \geq 0\\0, & if\:x < 0\end{cases}$$
C单元中的计算
C层的净输入为:
$$C\:=\:\displaystyle\sum\limits_i s_{i}x_{i}$$
这里,si是来自S单元的输出,xi是从S单元到C单元的固定权重。
最终输出如下:
$$C_{out}\:=\:\begin{cases}\frac{C}{a+C}, & if\:C > 0\\0, & otherwise\end{cases}$$
这里“a”是取决于网络性能的参数。