
人工神经网络 - 快速指南
人工神经网络 - 基本概念
神经网络是并行计算设备,它基本上是尝试创建大脑的计算机模型。其主要目标是开发一个比传统系统更快地执行各种计算任务的系统。这些任务包括模式识别和分类、逼近、优化和数据聚类。
什么是人工神经网络?
人工神经网络 (ANN) 是一种高效的计算系统,其核心主题借鉴了生物神经网络的类比。ANN 也被称为“人工神经系统”、“并行分布式处理系统”或“连接主义系统”。ANN 获取大量相互连接的单元,以某种模式允许单元之间进行通信。这些单元,也称为节点或神经元,是并行工作的简单处理器。
每个神经元都通过连接链路与其他神经元连接。每个连接链路都与一个权重相关联,该权重包含有关输入信号的信息。这是神经元解决特定问题最有用的信息,因为权重通常会激发或抑制正在传递的信号。每个神经元都有一个内部状态,称为激活信号。输出信号是在组合输入信号和激活规则后产生的,可以发送到其他单元。
ANN 的简史
ANN 的历史可以分为以下三个时期:
1940 年代至 1960 年代的 ANN
这个时期的几个关键发展如下:
1943 - 人们认为,神经网络的概念始于生理学家沃伦·麦卡洛克和数学家沃尔特·皮茨的工作,他们在 1943 年使用电路对简单的神经网络建模,以描述大脑中的神经元如何工作。
1949 - 唐纳德·赫布的著作《行为组织》阐述了一个事实,即一个神经元对另一个神经元的重复激活会增加它们每次使用时的强度。
1956 - 泰勒介绍了一种联想记忆网络。
1958 - 罗森布拉特发明了一种名为感知器的麦卡洛克-皮茨神经元模型的学习方法。
1960 - 伯纳德·维德罗和马西恩·霍夫开发了名为“ADALINE”和“MADALINE”的模型。
1960 年代至 1980 年代的 ANN
这个时期的几个关键发展如下:
1961 - 罗森布拉特进行了一次不成功的尝试,但提出了用于多层网络的“反向传播”方案。
1964 - 泰勒构建了一个在输出单元之间具有抑制的赢者通吃电路。
1969 - 明斯基和佩珀特发明了多层感知器 (MLP)。
1971 - 科霍宁开发了联想记忆。
1976 - 斯蒂芬·格罗斯伯格和盖尔·卡彭特开发了自适应谐振理论。
1980 年代至今的 ANN
这个时期的几个关键发展如下:
1982 - 最重要的发展是霍普菲尔德的能量方法。
1985 - 阿克利、欣顿和塞乔诺夫斯基开发了玻尔兹曼机。
1986 - 鲁梅尔哈特、欣顿和威廉姆斯引入了广义 delta 规则。
1988 - 科斯科开发了二元联想记忆 (BAM),并提出了 ANN 中的模糊逻辑概念。
历史回顾表明,该领域取得了重大进展。基于神经网络的芯片正在出现,并且正在开发对复杂问题的应用。毫无疑问,今天是神经网络技术的一个转型时期。
生物神经元
神经细胞(神经元)是一种特殊的生物细胞,它处理信息。据估计,神经元的数量巨大,大约为 1011,并且具有大量互连,大约为 1015。
示意图
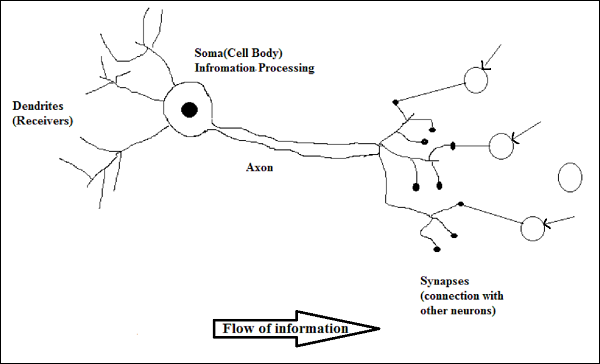
生物神经元的工作原理
如上图所示,一个典型的神经元由以下四个部分组成,我们可以用它们来解释其工作原理:
树突 - 它们是树状分支,负责接收来自与其连接的其他神经元的信息。换句话说,我们可以说它们像神经元的耳朵。
胞体 - 它是神经元的细胞体,负责处理从树突接收到的信息。
轴突 - 它就像一根电缆,神经元通过它发送信息。
突触 - 它是轴突和其他神经元树突之间的连接。
ANN 与 BNN
在查看人工神经网络 (ANN) 和生物神经网络 (BNN) 之间的区别之前,让我们先看看这两者之间基于术语的相似之处。
| 生物神经网络 (BNN) | 人工神经网络 (ANN) |
|---|---|
| 胞体 | 节点 |
| 树突 | 输入 |
| 突触 | 权重或互连 |
| 轴突 | 输出 |
下表显示了基于一些提到的标准对 ANN 和 BNN 的比较。
| 标准 | BNN | ANN |
|---|---|---|
| 处理 | 大规模并行,速度慢但优于 ANN | 大规模并行,速度快但劣于 BNN |
| 大小 | 1011 个神经元和 1015 个互连 | 102 到 104 个节点(主要取决于应用程序类型和网络设计者) |
| 学习 | 它们可以容忍模糊性 | 需要非常精确、结构化和格式化的数据才能容忍模糊性 |
| 容错性 | 即使部分损坏,性能也会下降 | 它能够实现强大的性能,因此具有容错的潜力 |
| 存储容量 | 将信息存储在突触中 | 将信息存储在连续的内存位置中 |
人工神经网络模型
下图表示 ANN 的通用模型及其处理过程。
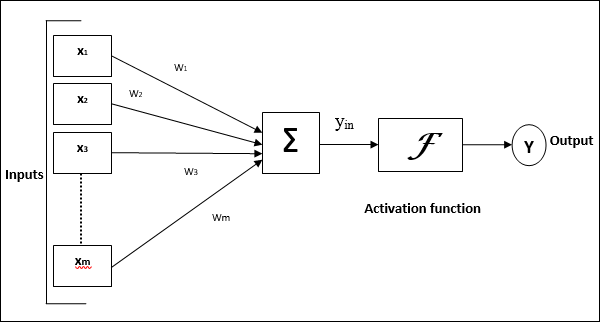
对于上述人工神经网络的通用模型,净输入的计算方法如下:
$$y_{in}\:=\:x_{1}.w_{1}\:+\:x_{2}.w_{2}\:+\:x_{3}.w_{3}\:\dotso\: x_{m}.w_{m}$$
即,净输入 $y_{in}\:=\:\sum_i^m\:x_{i}.w_{i}$
可以通过对净输入应用激活函数来计算输出。
$$Y\:=\:F(y_{in}) $$
输出 = 函数(计算的净输入)
人工神经网络 - 构建模块
ANN 的处理取决于以下三个构建模块:
- 网络拓扑
- 权重调整或学习
- 激活函数
本章将详细讨论 ANN 的这三个构建模块
网络拓扑
网络拓扑是网络及其节点和连接线的排列。根据拓扑结构,ANN 可以分为以下几种:
前馈网络
它是一个非循环网络,其处理单元/节点分层排列,并且一层中的所有节点都与前一层的节点连接。连接具有不同的权重。没有反馈环路,这意味着信号只能沿一个方向流动,从输入到输出。它可以分为以下两种类型:
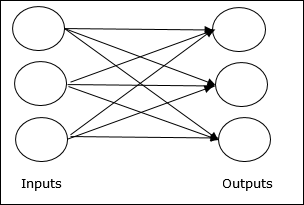
单层前馈网络 - 是指只有一个加权层的反馈式 ANN。换句话说,我们可以说输入层与输出层完全连接。
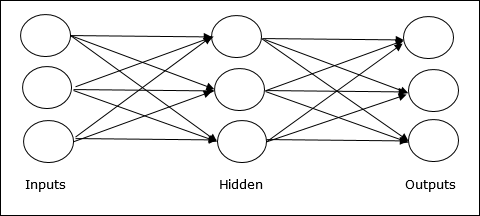
多层前馈网络 - 是指具有多个加权层的反馈式 ANN。由于该网络在输入层和输出层之间有一个或多个层,因此称为隐藏层。
反馈网络
顾名思义,反馈网络具有反馈路径,这意味着信号可以使用循环沿两个方向流动。这使其成为一个非线性动态系统,它会不断变化,直到达到平衡状态。它可以分为以下几种类型:
循环网络 - 它们是具有闭环的反馈网络。以下是两种类型的循环网络。
完全循环网络 - 它是最简单的神经网络架构,因为所有节点都连接到所有其他节点,并且每个节点都充当输入和输出。
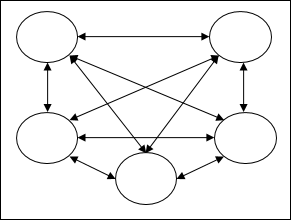
Jordan 网络 - 它是一个闭环网络,其中输出将作为反馈再次进入输入,如下面的图所示。
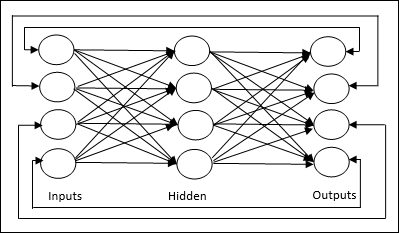
权重调整或学习
在人工神经网络中,学习是修改指定网络神经元之间连接权重的方法。ANN 中的学习可以分为三类,即监督学习、无监督学习和强化学习。
监督学习
顾名思义,这种类型的学习是在教师的监督下进行的。这个学习过程是依赖性的。
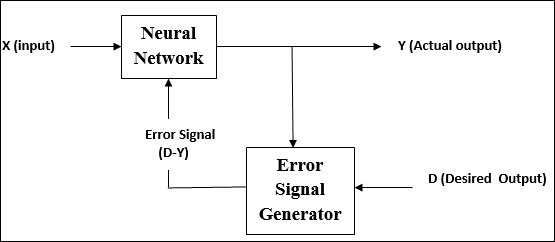
在监督学习下训练 ANN 期间,将输入向量呈现给网络,这将产生输出向量。该输出向量与所需输出向量进行比较。如果实际输出与所需输出向量之间存在差异,则会生成误差信号。根据此误差信号,调整权重,直到实际输出与所需输出匹配。
无监督学习
顾名思义,这种类型的学习是在没有教师监督的情况下进行的。这个学习过程是独立的。
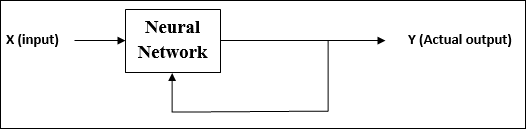
在无监督学习下训练 ANN 期间,将相似类型的输入向量组合起来形成聚类。当应用新的输入模式时,神经网络将给出指示输入模式所属类别的输出响应。
没有来自环境的关于所需输出是什么以及它是否正确的反馈。因此,在这种类型的学习中,网络本身必须从输入数据中发现模式和特征,以及输入数据对输出的关系。
强化学习
顾名思义,这种类型的学习用于加强或强化网络的一些评论信息。这个学习过程类似于监督学习,但是我们可能只有很少的信息。
在强化学习下训练网络期间,网络会从环境中接收一些反馈。这使其与监督学习有些相似。但是,此处获得的反馈是评估性的,而不是指导性的,这意味着与监督学习中一样,没有教师。在收到反馈后,网络会调整权重以在将来获得更好的评论信息。
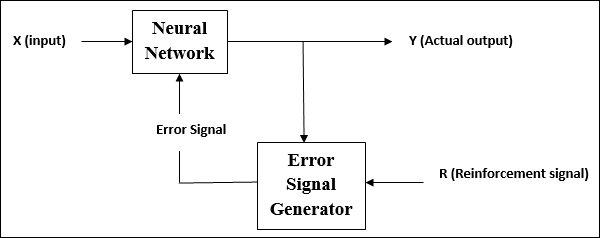
激活函数
它可以定义为施加在输入上的额外力量或努力以获得精确的输出。在 ANN 中,我们也可以对输入应用激活函数以获得精确的输出。以下是我们感兴趣的一些激活函数:
线性激活函数
它也称为恒等函数,因为它不执行任何输入编辑。它可以定义为:
$$F(x)\:=\:x$$
S 型激活函数
它有两种类型,如下所示:
二元 S 型函数 - 此激活函数将输入编辑在 0 和 1 之间。它具有正性质。它始终是有界的,这意味着其输出不能小于 0 且大于 1。它也是严格递增的,这意味着输入越多,输出越高。它可以定义为
$$F(x)\:=\:sigm(x)\:=\:\frac{1}{1\:+\:exp(-x)}$$
双极S型函数 − 此激活函数将输入编辑在-1和1之间。它可以是正数或负数。它始终是有界的,这意味着其输出不能小于-1且大于1。它也像S型函数一样严格递增。它可以定义为
$$F(x)\:=\:sigm(x)\:=\:\frac{2}{1\:+\:exp(-x)}\:-\:1\:=\:\frac{1\:-\:exp(x)}{1\:+\:exp(x)}$$
学习和适应
如前所述,人工神经网络完全受到生物神经系统,即人脑工作方式的启发。人脑最令人印象深刻的特点是学习,因此人工神经网络也获得了同样的特征。
人工神经网络中的学习是什么?
基本上,学习意味着根据环境的变化而进行自身改变和适应。人工神经网络是一个复杂的系统,更准确地说,它是一个复杂的适应性系统,它可以根据通过它的信息改变其内部结构。
为什么它很重要?
作为一个复杂的适应性系统,人工神经网络中的学习意味着处理单元能够由于环境的变化而改变其输入/输出行为。由于构建特定网络时激活函数以及输入/输出向量是固定的,因此人工神经网络中学习的重要性有所提高。现在要改变输入/输出行为,我们需要调整权重。
分类
它可以定义为通过查找相同类别样本之间的共同特征来学习将样本数据区分到不同类别中的过程。例如,为了执行人工神经网络的训练,我们有一些具有独特特征的训练样本,为了执行其测试,我们有一些具有其他独特特征的测试样本。分类是有监督学习的一个例子。
神经网络学习规则
我们知道,在人工神经网络学习过程中,要改变输入/输出行为,我们需要调整权重。因此,需要一种可以修改权重的方法。这些方法称为学习规则,它们只是算法或方程。以下是神经网络的一些学习规则:
Hebb学习规则
这条规则是最古老和最简单的规则之一,由Donald Hebb在1949年的著作《行为的组织》中提出。它是一种前馈、无监督学习。
基本概念 − 这条规则基于Hebb提出的一个假设,他写道:
“当细胞A的轴突足够接近于激发细胞B,并反复或持续地参与其激发时,一个或两个细胞中会发生一些生长过程或代谢变化,从而提高A作为激发B的细胞之一的效率。”
从上述假设中,我们可以得出结论:如果两个神经元同时激发,则它们之间的连接可能会加强;如果它们在不同时间激发,则连接可能会减弱。
数学公式 − 根据Hebb学习规则,以下是每次步长增加连接权重的公式。
$$\Delta w_{ji}(t)\:=\:\alpha x_{i}(t).y_{j}(t)$$
这里,$\Delta w_{ji}(t)$ = 在时间步长t时连接权重增加的增量
$\alpha$ = 正的常数学习率
$x_{i}(t)$ = 在时间步长t时来自突触前神经元的输入值
$y_{i}(t)$ = 在相同时间步长t时突触前神经元的输出
感知器学习规则
这条规则是由Rosenblatt提出的单层前馈网络的线性激活函数的误差校正监督学习算法。
基本概念 − 由于其监督性质,为了计算误差,需要比较期望/目标输出和实际输出。如果发现有任何差异,则必须更改连接权重。
数学公式 − 为了解释其数学公式,假设我们有'n'个有限输入向量x(n),以及其期望/目标输出向量t(n),其中n = 1到N。
现在可以计算输出'y',如前面根据净输入解释的那样,并应用于该净输入的激活函数可以表示为:
$$y\:=\:f(y_{in})\:=\:\begin{cases}1, & y_{in}\:>\:\theta \\0, & y_{in}\:\leqslant\:\theta\end{cases}$$
其中θ是阈值。
权重的更新可以在以下两种情况下进行:
情况一 − 当t ≠ y时,则
$$w(new)\:=\:w(old)\:+\;tx$$
情况二 − 当t = y时,则
权重不变
Delta学习规则(Widrow-Hoff规则)
它是由Bernard Widrow和Marcian Hoff提出的,也称为最小均方误差(LMS)方法,用于最小化所有训练模式的误差。它是一种具有连续激活函数的监督学习算法。
基本概念 − 这条规则的基础是梯度下降法,它会持续进行。Delta规则更新突触权重,以最小化输出单元的净输入和目标值之间的差异。
数学公式 − 为了更新突触权重,Delta规则由下式给出
$$\Delta w_{i}\:=\:\alpha\:.x_{i}.e_{j}$$
这里 $\Delta w_{i}$ = 第i个模式的权重变化;
$\alpha$ = 正的常数学习率;
$x_{i}$ = 来自突触前神经元的输入值;
$e_{j}$ = $(t\:-\:y_{in})$,期望/目标输出与实际输出$y_{in}$之间的差值
上述Delta规则仅适用于单个输出单元。
权重的更新可以在以下两种情况下进行:
情况一 − 当t ≠ y时,则
$$w(new)\:=\:w(old)\:+\:\Delta w$$
情况二 − 当t = y时,则
权重不变
竞争学习规则(胜者为王)
它关注的是无监督训练,其中输出节点试图相互竞争以表示输入模式。为了理解这个学习规则,我们必须理解如下所示的竞争网络:
竞争网络的基本概念 − 此网络类似于具有输出之间反馈连接的单层前馈网络。输出之间的连接是抑制类型的,用虚线表示,这意味着竞争者永远不会互相支持。
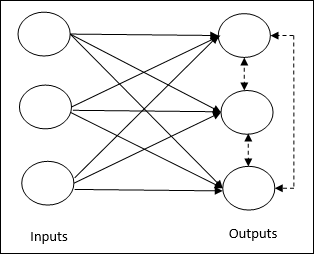
竞争学习规则的基本概念 − 如前所述,输出节点之间会存在竞争。因此,主要的概念是,在训练期间,对给定输入模式具有最高激活的输出单元将被宣布为获胜者。该规则也称为胜者为王,因为只有获胜神经元被更新,其余神经元保持不变。
数学公式 − 以下是此学习规则数学公式的三个重要因素:
获胜条件 − 假设如果神经元$y_{k}$ 想要获胜,则会有以下条件:
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k}\:>\:v_{j}\:for\:all\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
这意味着如果任何神经元,例如$y_{k}$ ,想要获胜,则其诱导局部场(求和单元的输出),例如$v_{k}$,必须是网络中所有其他神经元中最大的。
权重总和条件 − 对竞争学习规则的另一个约束是,对特定输出神经元的权重总和将为1。例如,如果我们考虑神经元k,则:
$$\displaystyle\sum\limits_{j}w_{kj}\:=\:1\:\:\:\:\:\:\:\:\:for\:all\:k$$
获胜者的权重变化 − 如果神经元对输入模式没有响应,则该神经元不会发生学习。但是,如果特定神经元获胜,则相应权重将按如下方式调整
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0, & if\:neuron\:k\:losses\end{cases}$$
这里$\alpha$是学习率。
这清楚地表明,我们正在通过调整其权重来偏向获胜神经元,如果存在神经元损失,则我们无需费心重新调整其权重。
Outstar学习规则
这条规则由Grossberg提出,它关注的是监督学习,因为期望输出是已知的。它也称为Grossberg学习。
基本概念 − 这条规则应用于按层排列的神经元。它专门设计用于产生p个神经元层的期望输出d。
数学公式 − 此规则中的权重调整计算如下
$$\Delta w_{j}\:=\:\alpha\:(d\:-\:w_{j})$$
这里d是期望神经元输出,$\alpha$是学习率。
监督学习
顾名思义,监督学习是在教师的监督下进行的。此学习过程是依赖性的。在监督学习下训练人工神经网络期间,输入向量将被呈现给网络,这将产生一个输出向量。此输出向量将与期望/目标输出向量进行比较。如果实际输出与期望/目标输出向量之间存在差异,则会生成误差信号。基于此误差信号,将调整权重,直到实际输出与期望输出匹配。
感知器
感知器由Frank Rosenblatt使用McCulloch和Pitts模型开发,是人工神经网络的基本操作单元。它采用监督学习规则,能够将数据分类为两类。
感知器的操作特性:它由具有任意数量输入以及可调节权重的单个神经元组成,但神经元的输出取决于阈值,为1或0。它还包括一个偏置,其权重始终为1。下图给出了感知器的示意图。
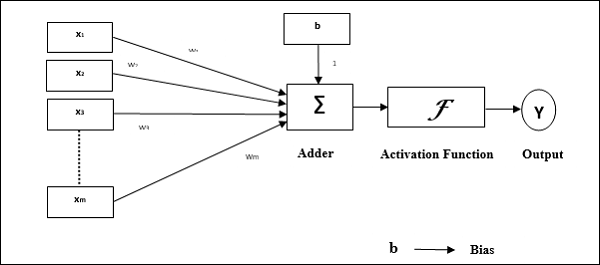
因此,感知器具有以下三个基本元素:
连接 − 它将有一组连接链接,这些链接携带权重,包括一个权重始终为1的偏置。
加法器 − 它在输入与其各自权重相乘后对其进行加法。
激活函数 − 它限制神经元的输出。最基本的激活函数是具有两个可能输出的Heaviside阶跃函数。如果输入为正,则此函数返回1;如果输入为负,则返回0。
训练算法
感知器网络可以针对单个输出单元以及多个输出单元进行训练。
单个输出单元的训练算法
步骤1 − 初始化以下内容以开始训练:
- 权重
- 偏置
- 学习率$\alpha$
为了简化计算,权重和偏置必须设置为0,学习率必须设置为1。
步骤2 − 当停止条件不为真时,继续步骤3-8。
步骤3 − 对于每个训练向量x,继续步骤4-6。
步骤 4 − 按如下方式激活每个输入单元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步骤 5 − 现在使用以下关系获得净输入 −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}.\:w_{i}$$
这里‘b’ 是偏置,‘n’ 是输入神经元的总数。
步骤 6 − 应用以下激活函数以获得最终输出。
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{in}\:\leqslant\:\theta\\-1 & if\:y_{in}\:<\:-\theta \end{cases}$$
步骤 7 − 按如下方式调整权重和偏置 −
情况 1 − 如果 y ≠ t,则
$$w_{i}(new)\:=\:w_{i}(old)\:+\:\alpha\:tx_{i}$$
$$b(new)\:=\:b(old)\:+\:\alpha t$$
情况 2 − 如果 y = t,则
$$w_{i}(new)\:=\:w_{i}(old)$$
$$b(new)\:=\:b(old)$$
这里‘y’ 是实际输出,‘t’ 是期望/目标输出。
步骤 8 − 测试停止条件,当权重没有变化时会发生。
多输出单元的训练算法
下图是用于多个输出类的感知器架构。
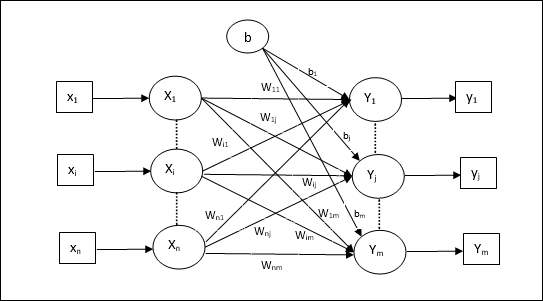
步骤1 − 初始化以下内容以开始训练:
- 权重
- 偏置
- 学习率$\alpha$
为了简化计算,权重和偏置必须设置为0,学习率必须设置为1。
步骤2 − 当停止条件不为真时,继续步骤3-8。
步骤3 − 对于每个训练向量x,继续步骤4-6。
步骤 4 − 按如下方式激活每个输入单元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步骤 5 − 使用以下关系获得净输入 −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}$$
这里‘b’ 是偏置,‘n’ 是输入神经元的总数。
步骤 6 − 应用以下激活函数以获得每个输出单元j = 1 到 m的最终输出 −
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{inj}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{inj}\:\leqslant\:\theta\\-1 & if\:y_{inj}\:<\:-\theta \end{cases}$$
步骤 7 − 如下调整x = 1 到 n和j = 1 到 m的权重和偏置 −
情况 1 − 如果 yj ≠ tj,则
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha\:t_{j}x_{i}$$
$$b_{j}(new)\:=\:b_{j}(old)\:+\:\alpha t_{j}$$
情况 2 − 如果 yj = tj,则
$$w_{ij}(new)\:=\:w_{ij}(old)$$
$$b_{j}(new)\:=\:b_{j}(old)$$
这里‘y’ 是实际输出,‘t’ 是期望/目标输出。
步骤 8 − 测试停止条件,当权重没有变化时会发生。
自适应线性神经元 (Adaline)
Adaline,即自适应线性神经元,是一个具有单个线性单元的网络。它由 Widrow 和 Hoff 于 1960 年开发。关于 Adaline 的一些要点如下 −
它使用双极激活函数。
它使用 delta 规则进行训练,以最小化实际输出与期望/目标输出之间的均方误差 (MSE)。
权重和偏置是可调整的。
架构
Adaline 的基本结构类似于感知器,它具有一个额外的反馈环路,借助该环路,实际输出与期望/目标输出进行比较。根据训练算法进行比较后,将更新权重和偏置。
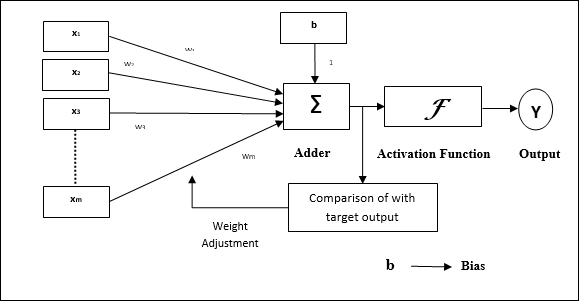
训练算法
步骤1 − 初始化以下内容以开始训练:
- 权重
- 偏置
- 学习率$\alpha$
为了简化计算,权重和偏置必须设置为0,学习率必须设置为1。
步骤2 − 当停止条件不为真时,继续步骤3-8。
步骤 3 − 对每个双极训练对s:t继续步骤 4-6。
步骤 4 − 按如下方式激活每个输入单元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步骤 5 − 使用以下关系获得净输入 −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{i}$$
这里‘b’ 是偏置,‘n’ 是输入神经元的总数。
步骤 6 − 应用以下激活函数以获得最终输出 −
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:\geqslant\:0 \\-1 & if\:y_{in}\:<\:0 \end{cases}$$
步骤 7 − 按如下方式调整权重和偏置 −
情况 1 − 如果 y ≠ t,则
$$w_{i}(new)\:=\:w_{i}(old)\:+\: \alpha(t\:-\:y_{in})x_{i}$$
$$b(new)\:=\:b(old)\:+\: \alpha(t\:-\:y_{in})$$
情况 2 − 如果 y = t,则
$$w_{i}(new)\:=\:w_{i}(old)$$
$$b(new)\:=\:b(old)$$
这里‘y’ 是实际输出,‘t’ 是期望/目标输出。
$(t\:-\;y_{in})$ 是计算出的误差。
步骤 8 − 测试停止条件,当权重没有变化或训练期间发生的最高权重变化小于指定的容差时会发生。
多自适应线性神经元 (Madaline)
Madaline,即多自适应线性神经元,是一个由许多 Adaline 并行组成的网络。它将具有单个输出单元。关于 Madaline 的一些要点如下 −
它就像一个多层感知器,其中 Adaline 充当输入层和 Madaline 层之间的隐藏单元。
输入层和 Adaline 层之间的权重和偏置(如我们在 Adaline 架构中看到的)是可调整的。
Adaline 和 Madaline 层的权重和偏置固定为 1。
可以使用 Delta 规则进行训练。
架构
Madaline 的架构由输入层的“n”个神经元、Adaline 层的“m”个神经元和 Madaline 层的 1 个神经元组成。Adaline 层可以被认为是隐藏层,因为它位于输入层和输出层(即 Madaline 层)之间。
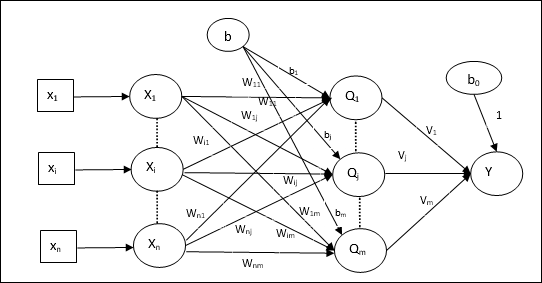
训练算法
到目前为止,我们知道只有输入层和 Adaline 层之间的权重和偏置需要调整,而 Adaline 层和 Madaline 层之间的权重和偏置是固定的。
步骤1 − 初始化以下内容以开始训练:
- 权重
- 偏置
- 学习率$\alpha$
为了简化计算,权重和偏置必须设置为0,学习率必须设置为1。
步骤2 − 当停止条件不为真时,继续步骤3-8。
步骤 3 − 对每个双极训练对s:t继续步骤 4-7。
步骤 4 − 按如下方式激活每个输入单元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步骤 5 − 使用以下关系获得每个隐藏层(即 Adaline 层)的净输入 −
$$Q_{inj}\:=\:b_{j}\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}\:\:\:j\:=\:1\:to\:m$$
这里‘b’ 是偏置,‘n’ 是输入神经元的总数。
步骤 6 − 应用以下激活函数以获得 Adaline 层和 Madaline 层的最终输出 −
$$f(x)\:=\:\begin{cases}1 & if\:x\:\geqslant\:0 \\-1 & if\:x\:<\:0 \end{cases}$$
隐藏层 (Adaline) 单元的输出
$$Q_{j}\:=\:f(Q_{inj})$$
网络的最终输出
$$y\:=\:f(y_{in})$$
即 $\:\:y_{inj}\:=\:b_{0}\:+\:\sum_{j = 1}^m\:Q_{j}\:v_{j}$
步骤 7 − 计算误差并如下调整权重 −
情况 1 − 如果 y ≠ t 且 t = 1,则
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\: \alpha(1\:-\:Q_{inj})x_{i}$$
$$b_{j}(new)\:=\:b_{j}(old)\:+\: \alpha(1\:-\:Q_{inj})$$
在这种情况下,将更新Qj上的权重,其中净输入接近 0,因为t = 1。
情况 2 − 如果 y ≠ t 且 t = -1,则
$$w_{ik}(new)\:=\:w_{ik}(old)\:+\: \alpha(-1\:-\:Q_{ink})x_{i}$$
$$b_{k}(new)\:=\:b_{k}(old)\:+\: \alpha(-1\:-\:Q_{ink})$$
在这种情况下,将更新Qk上的权重,其中净输入为正,因为t = -1。
这里‘y’ 是实际输出,‘t’ 是期望/目标输出。
情况 3 − 如果 y = t,则
权重不会发生变化。
步骤 8 − 测试停止条件,当权重没有变化或训练期间发生的最高权重变化小于指定的容差时会发生。
反向传播神经网络
反向传播神经网络 (BPN) 是一个多层神经网络,由输入层、至少一个隐藏层和输出层组成。顾名思义,在这个网络中将进行反向传播。通过比较目标输出和实际输出,在输出层计算出的误差将反向传播到输入层。
架构
如下图所示,BPN 的架构具有三个相互连接的层,这些层上带有权重。隐藏层和输出层也具有偏置,其权重始终为 1。从图中可以清楚地看出,BPN 的工作分为两个阶段。一个阶段将信号从输入层发送到输出层,另一个阶段将误差从输出层反向传播到输入层。
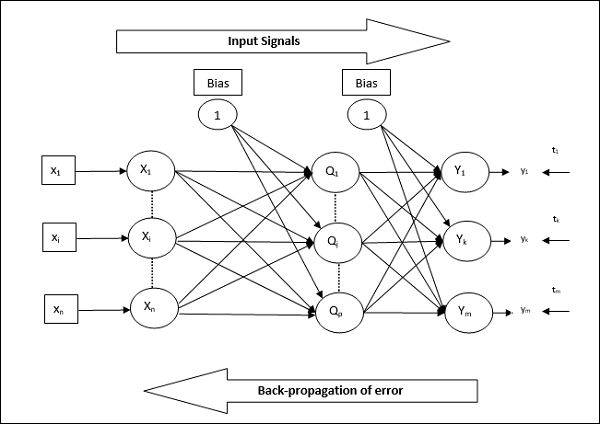
训练算法
对于训练,BPN 将使用二进制 sigmoid 激活函数。BPN 的训练将包含以下三个阶段。
阶段 1 − 前向传播阶段
阶段 2 − 误差反向传播
阶段 3 − 权重更新
所有这些步骤都将在以下算法中总结
步骤1 − 初始化以下内容以开始训练:
- 权重
- 学习率$\alpha$
为了简化计算,请取一些小的随机值。
步骤 2 − 当停止条件不成立时,继续步骤 3-11。
步骤 3 − 对每一对训练数据继续步骤 4-10。
阶段 1
步骤 4 − 每个输入单元接收输入信号xi 并将其发送到隐藏单元,所有i = 1 到 n
步骤 5 − 使用以下关系计算隐藏单元的净输入 −
$$Q_{inj}\:=\:b_{0j}\:+\:\sum_{i=1}^n x_{i}v_{ij}\:\:\:\:j\:=\:1\:to\:p$$
这里b0j是隐藏单元上的偏置,vij是从输入层的i单元到隐藏层的j单元的权重。
现在通过应用以下激活函数计算净输出
$$Q_{j}\:=\:f(Q_{inj})$$
将这些隐藏层单元的输出信号发送到输出层单元。
步骤 6 − 使用以下关系计算输出层单元的净输入 −
$$y_{ink}\:=\:b_{0k}\:+\:\sum_{j = 1}^p\:Q_{j}\:w_{jk}\:\:k\:=\:1\:to\:m$$
这里b0k是输出单元上的偏置,wjk是从隐藏层的j单元到输出层的k单元的权重。
通过应用以下激活函数计算净输出
$$y_{k}\:=\:f(y_{ink})$$
阶段 2
步骤 7 − 计算每个输出单元接收到的目标模式对应的误差校正项,如下所示 −
$$\delta_{k}\:=\:(t_{k}\:-\:y_{k})f^{'}(y_{ink})$$
在此基础上,更新权重和偏置,如下所示 −
$$\Delta v_{jk}\:=\:\alpha \delta_{k}\:Q_{ij}$$
$$\Delta b_{0k}\:=\:\alpha \delta_{k}$$
然后,将$\delta_{k}$反向传播到隐藏层。
步骤 8 − 现在每个隐藏单元将是来自输出单元的 delta 输入的总和。
$$\delta_{inj}\:=\:\displaystyle\sum\limits_{k=1}^m \delta_{k}\:w_{jk}$$
误差项可以计算如下 −
$$\delta_{j}\:=\:\delta_{inj}f^{'}(Q_{inj})$$
在此基础上,更新权重和偏置,如下所示 −
$$\Delta w_{ij}\:=\:\alpha\delta_{j}x_{i}$$
$$\Delta b_{0j}\:=\:\alpha\delta_{j}$$
阶段 3
步骤 9 − 每个输出单元(ykk = 1 到 m)更新权重和偏置,如下所示 −
$$v_{jk}(new)\:=\:v_{jk}(old)\:+\:\Delta v_{jk}$$
$$b_{0k}(new)\:=\:b_{0k}(old)\:+\:\Delta b_{0k}$$
步骤 10 − 每个输出单元(zjj = 1 到 p)更新权重和偏置,如下所示 −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\Delta w_{ij}$$
$$b_{0j}(new)\:=\:b_{0j}(old)\:+\:\Delta b_{0j}$$
步骤 11 − 检查停止条件,这可能是达到时期数或目标输出与实际输出匹配。
广义 Delta 学习规则
Delta 规则仅适用于输出层。另一方面,广义 Delta 规则(也称为反向传播规则)是创建隐藏层期望值的一种方法。
数学公式
对于激活函数$y_{k}\:=\:f(y_{ink})$,隐藏层和输出层上净输入的导数可以由下式给出
$$y_{ink}\:=\:\displaystyle\sum\limits_i\:z_{i}w_{jk}$$
并且$\:\:y_{inj}\:=\:\sum_i x_{i}v_{ij}$
现在必须最小化的误差是
$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2$$
使用链式法则,我们有
$$\frac{\partial E}{\partial w_{jk}}\:=\:\frac{\partial }{\partial w_{jk}}(\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2)$$
$$=\:\frac{\partial }{\partial w_{jk}}\lgroup\frac{1}{2}[t_{k}\:-\:t(y_{ink})]^2\rgroup$$
$$=\:-[t_{k}\:-\:y_{k}]\frac{\partial }{\partial w_{jk}}f(y_{ink})$$
$$=\:-[t_{k}\:-\:y_{k}]f(y_{ink})\frac{\partial }{\partial w_{jk}}(y_{ink})$$
$$=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})z_{j}$$
现在让我们说$\delta_{k}\:=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})$
连接到隐藏单元zj的权重可以由下式给出 −
$$\frac{\partial E}{\partial v_{ij}}\:=\:- \displaystyle\sum\limits_{k} \delta_{k}\frac{\partial }{\partial v_{ij}}\:(y_{ink})$$
代入$y_{ink}$的值,我们将得到以下结果
$$\delta_{j}\:=\:-\displaystyle\sum\limits_{k}\delta_{k}w_{jk}f^{'}(z_{inj})$$
权重更新可以如下进行 −
对于输出单元 −
$$\Delta w_{jk}\:=\:-\alpha\frac{\partial E}{\partial w_{jk}}$$
$$=\:\alpha\:\delta_{k}\:z_{j}$$
对于隐藏单元 −
$$\Delta v_{ij}\:=\:-\alpha\frac{\partial E}{\partial v_{ij}}$$
$$=\:\alpha\:\delta_{j}\:x_{i}$$
无监督学习
顾名思义,这种类型的学习是在没有教师监督的情况下进行的。这个学习过程是独立的。在无监督学习下训练 ANN 期间,将类似类型的输入向量组合起来形成聚类。当应用新的输入模式时,神经网络会给出指示输入模式所属类别的输出响应。在这里,不会有来自环境的反馈来指示期望输出是什么以及它是否正确。因此,在这种类型的学习中,网络本身必须从输入数据中发现模式、特征以及输入数据与输出之间的关系。
赢者通吃网络
这类网络基于竞争学习规则,并采用选择总输入量最大的神经元作为获胜者的策略。输出神经元之间的连接显示了它们之间的竞争,其中一个神经元将处于“ON”状态,这意味着它获胜,而其他神经元将处于“OFF”状态。
以下是基于此简单概念使用无监督学习的一些网络。
Hamming 网络
在大多数使用无监督学习的神经网络中,计算距离和进行比较是必不可少的。这种网络是 Hamming 网络,对于每个给定的输入向量,它将被聚类到不同的组中。以下是 Hamming 网络的一些重要特征:
Lippmann 于 1987 年开始研究 Hamming 网络。
它是一个单层网络。
输入可以是二进制 {0, 1} 或双极性 {-1, 1}。
网络的权重由示例向量计算。
它是一个固定权重网络,这意味着即使在训练过程中权重也会保持不变。
Max 网络
这也是一个固定权重网络,用作选择具有最高输入的节点的子网。所有节点都完全互连,并且在所有这些加权互连中存在对称权重。
架构
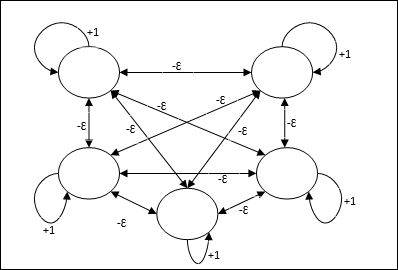
它使用迭代过程的机制,每个节点通过连接从所有其他节点接收抑制性输入。值最大的单个节点将处于活动状态或获胜状态,所有其他节点的激活将处于非活动状态。Max 网络使用恒等激活函数,其公式为 $$f(x)\:=\:\begin{cases}x & if\:x > 0\\0 & if\:x \leq 0\end{cases}$$
该网络的任务是通过 +1 的自激权重和互抑制幅度来完成的,该幅度设置为 [0 < ɛ < $\frac{1}{m}$],其中“m”是节点的总数。
人工神经网络中的竞争学习
它关注无监督训练,其中输出节点相互竞争以表示输入模式。为了理解这个学习规则,我们必须理解竞争网络,解释如下:
竞争网络的基本概念
这个网络就像一个单层前馈网络,在输出之间具有反馈连接。输出之间的连接是抑制类型的,用虚线表示,这意味着竞争者永远不会相互支持。
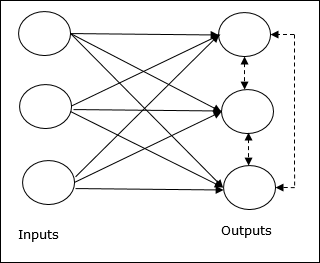
竞争学习规则的基本概念
如前所述,输出节点之间会有竞争,因此主要概念是:在训练期间,对给定输入模式具有最高激活的输出单元将被宣布为获胜者。此规则也称为赢者通吃,因为只有获胜神经元会更新,其余神经元保持不变。
数学公式
以下是此学习规则数学公式的三个重要因素:
获胜条件
假设如果神经元yk想要获胜,则会有以下条件:
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k} > v_{j}\:for\:all\:\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
这意味着如果任何神经元,例如yk想要获胜,则其诱导局部场(求和单元的输出),例如vk,必须是网络中所有其他神经元中最大的。
权重总和条件
竞争学习规则的另一个约束是特定输出神经元的权重总和将为 1。例如,如果我们考虑神经元k,则
$$\displaystyle\sum\limits_{k} w_{kj}\:=\:1\:\:\:\:for\:all\:\:k$$
获胜者的权重变化
如果神经元对输入模式没有响应,则该神经元不会发生学习。但是,如果特定神经元获胜,则相应权重将如下调整:
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0 & if\:neuron\:k\:losses\end{cases}$$
这里$\alpha$是学习率。
这清楚地表明,我们通过调整其权重来偏向获胜神经元,如果神经元失败,则我们无需重新调整其权重。
K 均值聚类算法
K 均值是最流行的聚类算法之一,其中我们使用分区过程的概念。我们从初始分区开始,并反复将模式从一个聚类移动到另一个聚类,直到我们得到令人满意的结果。
算法
步骤 1 - 选择k个点作为初始质心。初始化k个原型(w1,…,wk),例如,我们可以通过随机选择的输入向量来识别它们:
$$W_{j}\:=\:i_{p},\:\:\: where\:j\:\in \lbrace1,....,k\rbrace\:and\:p\:\in \lbrace1,....,n\rbrace$$
每个聚类Cj都与原型wj相关联。
步骤 2 - 重复步骤 3-5,直到 E 不再减少,或者聚类成员资格不再改变。
步骤 3 - 对于每个输入向量ip,其中p ∈ {1,…,n},将ip放入具有最近原型的聚类Cj*中,该原型具有以下关系:
$$|i_{p}\:-\:w_{j*}|\:\leq\:|i_{p}\:-\:w_{j}|,\:j\:\in \lbrace1,....,k\rbrace$$
步骤 4 - 对于每个聚类Cj,其中j ∈ { 1,…,k},更新原型wj为当前在Cj中所有样本的质心,以便
$$w_{j}\:=\:\sum_{i_{p}\in C_{j}}\frac{i_{p}}{|C_{j}|}$$
步骤 5 - 计算总量化误差如下:
$$E\:=\:\sum_{j=1}^k\sum_{i_{p}\in w_{j}}|i_{p}\:-\:w_{j}|^2$$
Neocognitron
它是一个多层前馈网络,由 Fukushima 于 20 世纪 80 年代开发。该模型基于监督学习,用于视觉模式识别,主要是手写字符。它基本上是 Cognitron 网络的扩展,Cognitron 网络也是由 Fukushima 于 1975 年开发的。
架构
它是一个分层网络,包含许多层,并且这些层中存在局部连接模式。
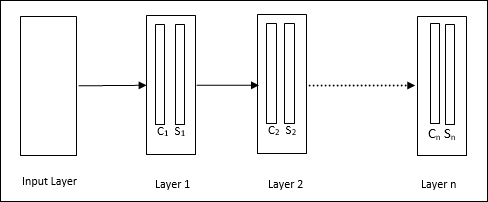
正如我们在上图中看到的,neocognitron 被分成不同的连接层,每一层都有两个单元。这些单元的解释如下:
S 单元 - 它被称为简单单元,经过训练可以响应特定模式或一组模式。
C 单元 - 它被称为复杂单元,它结合了来自 S 单元的输出,同时减少了每个阵列中的单元数量。换句话说,C 单元会置换 S 单元的输出。
训练算法
Neocognitron 的训练被发现是逐层进行的。从输入层到第一层的权重被训练并冻结。然后,训练从第一层到第二层的权重,依此类推。S 单元和 C 单元之间的内部计算取决于来自前几层的权重。因此,我们可以说训练算法取决于 S 单元和 C 单元上的计算。
S 单元中的计算
S 单元拥有从前一层接收的兴奋性信号,并拥有在同一层内获得的抑制性信号。
$$\theta=\:\sqrt{\sum\sum t_{i} c_{i}^2}$$
这里,ti是固定权重,ci是来自 C 单元的输出。
S 单元的缩放输入可以计算如下:
$$x\:=\:\frac{1\:+\:e}{1\:+\:vw_{0}}\:-\:1$$
这里,$e\:=\:\sum_i c_{i}w_{i}$
wi是从 C 单元到 S 单元的调整权重。
w0是输入和 S 单元之间可调整的权重。
v是来自 C 单元的兴奋性输入。
输出信号的激活为:
$$s\:=\:\begin{cases}x, & if\:x \geq 0\\0, & if\:x < 0\end{cases}$$
C 单元中的计算
C 层的净输入为
$$C\:=\:\displaystyle\sum\limits_i s_{i}x_{i}$$
这里,si是来自 S 单元的输出,xi是从 S 单元到 C 单元的固定权重。
最终输出如下:
$$C_{out}\:=\:\begin{cases}\frac{C}{a+C}, & if\:C > 0\\0, & otherwise\end{cases}$$
这里‘a’是取决于网络性能的参数。
学习向量量化
学习向量量化 (LVQ) 与向量量化 (VQ) 和 Kohonen 自组织映射 (KSOM) 不同,它基本上是一个使用监督学习的竞争网络。我们可以将其定义为对模式进行分类的过程,其中每个输出单元代表一个类别。由于它使用监督学习,因此网络将获得一组具有已知分类的训练模式以及输出类别的初始分布。完成训练过程后,LVQ 将通过将其分配到与输出单元相同的类别来对输入向量进行分类。
架构
下图显示了 LVQ 的体系结构,它与 KSOM 的体系结构非常相似。我们可以看到,有“n”个输入单元和“m”个输出单元。各层完全互连,并带有权重。
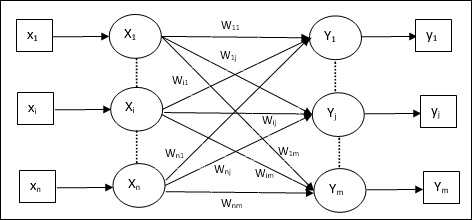
使用的参数
以下是 LVQ 训练过程以及流程图中使用的参数:
x = 训练向量 (x1,...,xi,...,xn)
T = 训练向量x的类别
wj = 第jth个输出单元的权重向量
Cj = 与第jth个输出单元相关的类别
训练算法
步骤 1 - 初始化参考向量,可以按如下方式完成:
步骤 1(a) - 从给定的训练向量集中,取前“m”(聚类数)个训练向量并将其用作权重向量。其余向量可用于训练。
步骤 1(b) - 随机分配初始权重和分类。
步骤 1(c) - 应用 K 均值聚类方法。
步骤 2 - 初始化参考向量 $\alpha$
步骤 3 - 如果未满足停止此算法的条件,则继续执行步骤 4-9。
步骤 4 - 对于每个训练输入向量x,执行步骤 5-6。
步骤 5 - 计算j = 1 到 m和i = 1 到 n的欧几里得距离的平方
$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$
步骤 6 - 获取获胜单元J,其中D(j)最小。
步骤 7 − 使用以下关系计算获胜单元的新权重 −
如果 T = Cj,则 $w_{j}(new)\:=\:w_{j}(old)\:+\:\alpha[x\:-\:w_{j}(old)]$
如果 T ≠ Cj,则 $w_{j}(new)\:=\:w_{j}(old)\:-\:\alpha[x\:-\:w_{j}(old)]$
步骤 8 − 降低学习率 $\alpha$。
步骤 9 − 测试停止条件。它可能是如下所示 −
- 达到最大迭代次数。
- 学习率降低到可忽略不计的值。
流程图
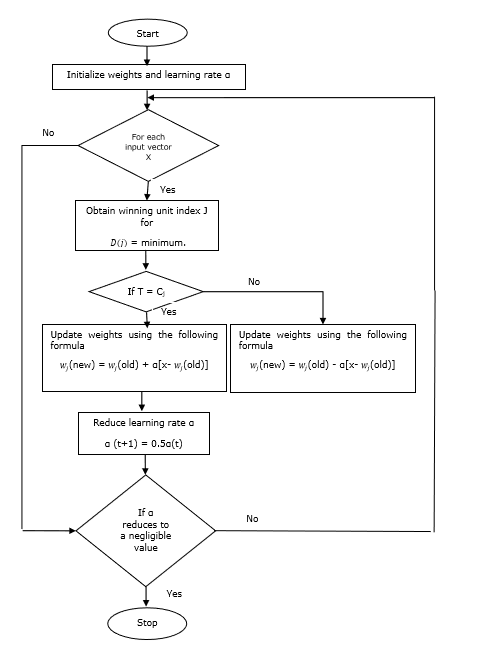
变体
Kohonen 开发了另外三个变体,即 LVQ2、LVQ2.1 和 LVQ3。由于获胜单元和亚军单元都会学习,这三个变体的复杂度都高于 LVQ。
LVQ2
如上所述,LVQ 其他变体的概念是由窗口构成的。此窗口将基于以下参数 −
x − 当前输入向量
yc − 最接近 x 的参考向量
yr − 另一个参考向量,它是次接近 x 的向量
dc − 从 x 到 yc 的距离
dr − 从 x 到 yr 的距离
如果输入向量 x 落入窗口内,则
$$\frac{d_{c}}{d_{r}}\:>\:1\:-\:\theta\:\:and\:\:\frac{d_{r}}{d_{c}}\:>\:1\:+\:\theta$$
这里,$\theta$ 是训练样本的数量。
可以使用以下公式进行更新 −
$y_{c}(t\:+\:1)\:=\:y_{c}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c}(t)]$ (属于不同类别)
$y_{r}(t\:+\:1)\:=\:y_{r}(t)\:+\:\alpha(t)[x(t)\:-\:y_{r}(t)]$ (属于同一类别)
这里$\alpha$是学习率。
LVQ2.1
在 LVQ2.1 中,我们将取两个最接近的向量,即 yc1 和 yc2,窗口条件如下 −
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)$$
$$Max\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:<\:(1\:+\:\theta)$$
可以使用以下公式进行更新 −
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c1}(t)]$ (属于不同类别)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c2}(t)]$ (属于同一类别)
这里,$\alpha$ 是学习率。
LVQ3
在 LVQ3 中,我们将取两个最接近的向量,即 yc1 和 yc2,窗口条件如下 −
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)(1\:+\:\theta)$$
这里 $\theta\approx 0.2$
可以使用以下公式进行更新 −
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\beta(t)[x(t)\:-\:y_{c1}(t)]$ (属于不同类别)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\beta(t)[x(t)\:-\:y_{c2}(t)]$ (属于同一类别)
这里 $\beta$ 是学习率 $\alpha$ 的倍数,并且 $\beta\:=\:m \alpha(t)$,对于每个 0.1 < m < 0.5
自适应谐振理论
该网络由 Stephen Grossberg 和 Gail Carpenter 于 1987 年开发。它基于竞争并使用无监督学习模型。自适应谐振理论 (ART) 网络顾名思义,始终对新学习开放(自适应),而不会丢失旧模式(谐振)。基本上,ART 网络是一个向量分类器,它接受一个输入向量并将其分类到一个类别中,这取决于它最类似于哪个存储模式。
工作原理
ART 分类的主要操作可以分为以下阶段 −
识别阶段 − 将输入向量与输出层每个节点上呈现的分类进行比较。如果神经元的输出与应用的分类最佳匹配,则其输出变为“1”,否则变为“0”。
比较阶段 − 在此阶段,将输入向量与比较层向量进行比较。重置条件是相似度小于警戒参数。
搜索阶段 − 在此阶段,网络将搜索上述阶段中完成的重置和匹配。因此,如果没有重置并且匹配相当好,则分类完成。否则,将重复该过程,并且必须发送其他存储模式以找到正确的匹配。
ART1
它是一种 ART 类型,旨在聚类二进制向量。我们可以通过其架构来了解这一点。
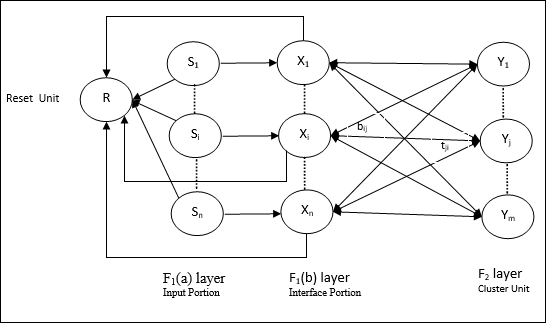
ART1 的架构
它包含以下两个单元 −
计算单元 − 它由以下部分组成 −
输入单元 (F1 层) − 它进一步具有以下两个部分 −
F1(a) 层(输入部分) − 在 ART1 中,除了只有输入向量之外,此部分没有处理。它连接到 F1(b) 层(接口部分)。
F1(b) 层(接口部分) − 此部分将来自输入部分的信号与 F2 层的信号组合。F1(b) 层通过自下而上的权重 bij 连接到 F2 层,F2 层通过自上而下的权重 tji 连接到 F1(b) 层。
聚类单元 (F2 层) − 这是一个竞争层。选择具有最大净输入的单元来学习输入模式。所有其他聚类单元的激活都设置为 0。
重置机制 − 此机制的工作基于自上而下的权重和输入向量之间的相似性。现在,如果这种相似程度小于警戒参数,则不允许聚类学习模式,并且会发生重置。
补充单元 − 实际上,重置机制的问题在于,F2 层必须在某些条件下被抑制,并且在发生某些学习时也必须可用。这就是为什么添加了两个补充单元,即 G1 和 G2,以及重置单元 R。它们被称为增益控制单元。这些单元接收并向网络中存在的其他单元发送信号。“+”表示兴奋性信号,“−”表示抑制性信号。
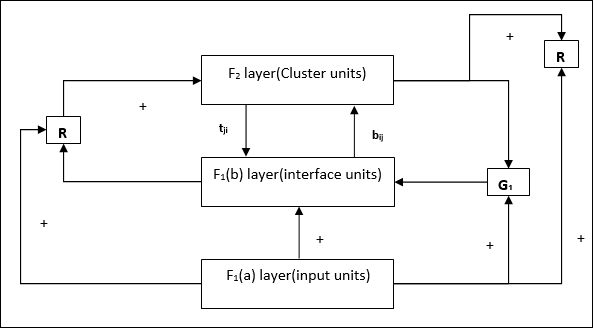
使用的参数
使用以下参数 −
n − 输入向量中分量的数量
m − 可以形成的最大聚类数
bij − 从 F1(b) 到 F2 层的权重,即自下而上的权重
tji − 从 F2 到 F1(b) 层的权重,即自上而下的权重
ρ − 警戒参数
||x|| − 向量 x 的范数
算法
步骤 1 − 初始化学习率、警戒参数和权重,如下所示 −
$$\alpha\:>\:1\:\:and\:\:0\:<\rho\:\leq\:1$$
$$0\:<\:b_{ij}(0)\:<\:\frac{\alpha}{\alpha\:-\:1\:+\:n}\:\:and\:\:t_{ij}(0)\:=\:1$$
步骤 2 − 当停止条件不为真时,继续步骤 3-9。
步骤 3 − 对于每个训练输入,继续步骤 4-6。
步骤 4 − 设置所有 F1(a) 和 F1 单元的激活,如下所示
F2 = 0 和 F1(a) = 输入向量
步骤 5 − 来自 F1(a) 到 F1(b) 层的输入信号必须像这样发送
$$s_{i}\:=\:x_{i}$$
步骤 6 − 对于每个被抑制的 F2 节点
$y_{j}\:=\:\sum_i b_{ij}x_{i}$ 条件是 yj ≠ -1
步骤 7 − 当重置为真时,执行步骤 8-10。
步骤 8 − 找到 J,对于所有节点 j,yJ ≥ yj
步骤 9 − 再次计算 F1(b) 上的激活,如下所示
$$x_{i}\:=\:sitJi$$
步骤 10 − 现在,在计算向量 x 和向量 s 的范数后,我们需要检查重置条件,如下所示 −
如果 ||x||/ ||s|| < 警戒参数 ρ,则抑制节点 J 并转到步骤 7
否则如果 ||x||/ ||s|| ≥ 警戒参数 ρ,则继续。
步骤 11 − 节点 J 的权重更新可以如下进行 −
$$b_{ij}(new)\:=\:\frac{\alpha x_{i}}{\alpha\:-\:1\:+\:||x||}$$
$$t_{ij}(new)\:=\:x_{i}$$
步骤 12 − 必须检查算法的停止条件,它可能是如下所示 −
- 权重没有任何变化。
- 未对单元执行重置。
- 达到最大迭代次数。
Kohonen自组织特征映射
假设我们有一些任意维度的模式,但是我们需要将它们转换为一维或二维。然后,特征映射过程对于将宽模式空间转换为典型的特征空间非常有用。现在,问题出现了,为什么我们需要自组织特征映射?原因是,除了能够将任意维度转换为一维或二维之外,它还必须具有保持邻域拓扑的能力。
Kohonen SOM 中的邻域拓扑
可以有多种拓扑结构,但是以下两种拓扑结构使用得最多 −
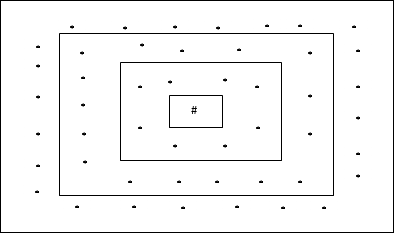
矩形网格拓扑
这种拓扑在距离 2 网格中具有 24 个节点,在距离 1 网格中具有 16 个节点,在距离 0 网格中具有 8 个节点,这意味着每个矩形网格之间的差值为 8 个节点。获胜单元用 # 表示。
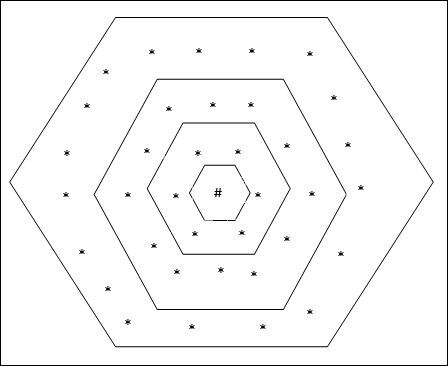
六边形网格拓扑
这种拓扑在距离 2 网格中具有 18 个节点,在距离 1 网格中具有 12 个节点,在距离 0 网格中具有 6 个节点,这意味着每个矩形网格之间的差值为 6 个节点。获胜单元用 # 表示。
架构
KSOM 的架构类似于竞争网络的架构。借助前面讨论的邻域方案,可以在网络的扩展区域进行训练。
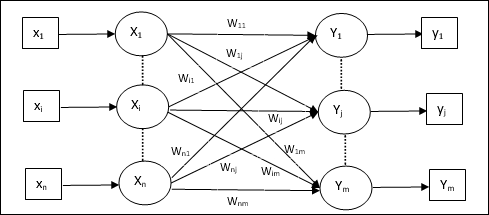
训练算法
步骤 1 − 初始化权重、学习率 α 和邻域拓扑方案。
步骤 2 − 当停止条件不为真时,继续步骤 3-9。
步骤 3 − 对于每个输入向量 x,继续步骤 4-6。
步骤 4 − 计算 j = 1 到 m 的欧几里德距离的平方
$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n \displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$
步骤 5 − 获取获胜单元 J,其中 D(j) 最小。
步骤 6 − 使用以下关系计算获胜单元的新权重 −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha[x_{i}\:-\:w_{ij}(old)]$$
步骤 7 − 使用以下关系更新学习率 α −
$$\alpha(t\:+\:1)\:=\:0.5\alpha t$$
步骤 8 − 减小拓扑方案的半径。
步骤 9 − 检查网络的停止条件。
联想记忆网络
这些类型的神经网络基于模式关联工作,这意味着它们可以存储不同的模式,并且在输出时,它们可以通过将它们与给定的输入模式匹配来产生存储的模式之一。这些类型的存储器也称为内容寻址存储器 (CAM)。联想存储器将存储的模式作为数据文件进行并行搜索。
以下是我们可以观察到的两种类型的联想存储器 −
- 自联想记忆
- 异联想记忆
自联想记忆
这是一个单层神经网络,其中输入训练向量和输出目标向量相同。确定权重,以便网络存储一组模式。
架构
如下图所示,自联想记忆网络的架构具有‘n’个输入训练向量和同样数量的‘n’个输出目标向量。
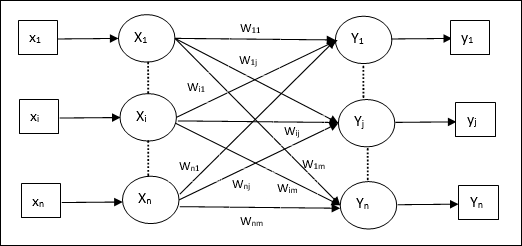
训练算法
该网络使用Hebb学习规则或Delta学习规则进行训练。
步骤 1 − 将所有权重初始化为零,即wij = 0 (i = 1 到 n, j = 1 到 n)
步骤 2 − 对每个输入向量执行步骤 3-4。
步骤 3 − 按如下方式激活每个输入单元:
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步骤 4 − 按如下方式激活每个输出单元:
$$y_{j}\:=\:s_{j}\:(j\:=\:1\:to\:n)$$
步骤 5 − 按如下方式调整权重:
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:x_{i}y_{j}$$
测试算法
步骤 1 − 设置Hebb规则训练期间获得的权重。
步骤 2 − 对每个输入向量执行步骤 3-5。
步骤 3 − 将输入单元的激活设置为与输入向量相同。
步骤 4 − 计算每个输出单元j = 1 到 n的净输入
$$y_{inj}\:=\:\displaystyle\sum\limits_{i=1}^n x_{i}w_{ij}$$
步骤 5 − 应用以下激活函数来计算输出
$$y_{j}\:=\:f(y_{inj})\:=\:\begin{cases}+1 & if\:y_{inj}\:>\:0\\-1 & if\:y_{inj}\:\leqslant\:0\end{cases}$$
异联想记忆
与自联想记忆网络类似,这也是一个单层神经网络。但是,在这个网络中,输入训练向量和输出目标向量并不相同。权重被确定,以便网络存储一组模式。异联想网络本质上是静态的,因此不会有非线性或延迟操作。
架构
如下图所示,异联想记忆网络的架构具有‘n’个输入训练向量和‘m’个输出目标向量。
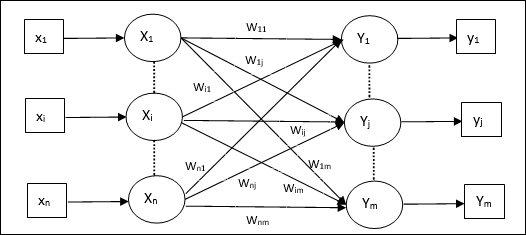
训练算法
该网络使用Hebb学习规则或Delta学习规则进行训练。
步骤 1 − 将所有权重初始化为零,即wij = 0 (i = 1 到 n, j = 1 到 m)
步骤 2 − 对每个输入向量执行步骤 3-4。
步骤 3 − 按如下方式激活每个输入单元:
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步骤 4 − 按如下方式激活每个输出单元:
$$y_{j}\:=\:s_{j}\:(j\:=\:1\:to\:m)$$
步骤 5 − 按如下方式调整权重:
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:x_{i}y_{j}$$
测试算法
步骤 1 − 设置Hebb规则训练期间获得的权重。
步骤 2 − 对每个输入向量执行步骤 3-5。
步骤 3 − 将输入单元的激活设置为与输入向量相同。
步骤 4 − 计算每个输出单元j = 1 到 m的净输入:
$$y_{inj}\:=\:\displaystyle\sum\limits_{i=1}^n x_{i}w_{ij}$$
步骤 5 − 应用以下激活函数来计算输出
$$y_{j}\:=\:f(y_{inj})\:=\:\begin{cases}+1 & if\:y_{inj}\:>\:0\\0 & if\:y_{inj}\:=\:0\\-1 & if\:y_{inj}\:<\:0\end{cases}$$
人工神经网络 - Hopfield网络
Hopfield神经网络由John J. Hopfield博士于1982年发明。它由单层组成,包含一个或多个完全连接的循环神经元。Hopfield网络通常用于自关联和优化任务。
离散Hopfield网络
Hopfield网络以离散的方式运行,换句话说,可以认为输入和输出模式是离散向量,其性质可以是二进制(0,1)或双极性(+1, -1)。该网络具有对称权重,没有自连接,即wij = wji和wii = 0。
架构
以下是一些关于离散Hopfield网络需要注意的重要事项:
该模型由具有一个反相输出和一个非反相输出的神经元组成。
每个神经元的输出应该是其他神经元的输入,但不能是自身的输入。
权重/连接强度由wij表示。
连接可以是兴奋性的,也可以是抑制性的。如果神经元的输出与其输入相同,则为兴奋性,否则为抑制性。
权重应是对称的,即wij = wji
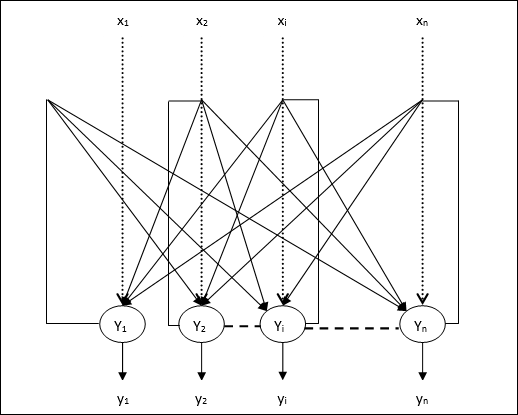
从Y1到Y2、Yi和Yn的输出分别具有权重w12、w1i和w1n。类似地,其他弧线也具有其上的权重。
训练算法
在离散Hopfield网络的训练过程中,权重将被更新。众所周知,我们可以具有二进制输入向量和双极性输入向量。因此,在这两种情况下,权重更新都可以通过以下关系完成
情况 1 − 二进制输入模式
对于一组二进制模式s(p), p = 1 到 P
这里,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
权重矩阵由下式给出
$$w_{ij}\:=\:\sum_{p=1}^P[2s_{i}(p)-\:1][2s_{j}(p)-\:1]\:\:\:\:\:for\:i\:\neq\:j$$
情况 2 − 双极性输入模式
对于一组二进制模式s(p), p = 1 到 P
这里,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
权重矩阵由下式给出
$$w_{ij}\:=\:\sum_{p=1}^P[s_{i}(p)][s_{j}(p)]\:\:\:\:\:for\:i\:\neq\:j$$
测试算法
步骤 1 − 初始化权重,这些权重是通过使用Hebbian原理从训练算法中获得的。
步骤 2 − 如果网络的激活未稳定,则执行步骤 3-9。
步骤 3 − 对于每个输入向量X,执行步骤 4-8。
步骤 4 − 将网络的初始激活设置为等于外部输入向量X,如下所示:
$$y_{i}\:=\:x_{i}\:\:\:for\:i\:=\:1\:to\:n$$
步骤 5 − 对于每个单元Yi,执行步骤 6-9。
步骤 6 − 按如下方式计算网络的净输入:
$$y_{ini}\:=\:x_{i}\:+\:\displaystyle\sum\limits_{j}y_{j}w_{ji}$$
步骤 7 − 对净输入应用以下激活函数来计算输出:
$$y_{i}\:=\begin{cases}1 & if\:y_{ini}\:>\:\theta_{i}\\y_{i} & if\:y_{ini}\:=\:\theta_{i}\\0 & if\:y_{ini}\:<\:\theta_{i}\end{cases}$$
这里$\theta_{i}$是阈值。
步骤 8 − 将此输出yi广播到所有其他单元。
步骤 9 − 测试网络的连接。
能量函数评估
能量函数定义为系统的状态的有界且非递增函数。
能量函数Ef,也称为Lyapunov函数,确定离散Hopfield网络的稳定性,其特征如下:
$$E_{f}\:=\:-\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^n y_{i}y_{j}w_{ij}\:-\:\displaystyle\sum\limits_{i=1}^n x_{i}y_{i}\:+\:\displaystyle\sum\limits_{i=1}^n \theta_{i}y_{i}$$
条件 − 在稳定网络中,每当节点状态发生变化时,上述能量函数都会减小。
假设当节点i的状态从$y_i^{(k)}$变为$y_i^{(k\:+\:1)}$时,能量变化$\Delta E_{f}$由以下关系给出
$$\Delta E_{f}\:=\:E_{f}(y_i^{(k+1)})\:-\:E_{f}(y_i^{(k)})$$
$$=\:-\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{ij}y_i^{(k)}\:+\:x_{i}\:-\:\theta_{i}\end{array}\right)(y_i^{(k+1)}\:-\:y_i^{(k)})$$
$$=\:-\:(net_{i})\Delta y_{i}$$
这里$\Delta y_{i}\:=\:y_i^{(k\:+\:1)}\:-\:y_i^{(k)}$
能量变化取决于一次只有一个单元可以更新其激活这一事实。
连续Hopfield网络
与离散Hopfield网络相比,连续网络具有连续变量的时间。它也用于自关联和优化问题,例如旅行商问题。
模型 − 可以通过添加电子元件(例如放大器)来构建模型或架构,这些元件可以将输入电压映射到通过S型激活函数的输出电压。
能量函数评估
$$E_f = \frac{1}{2}\displaystyle\sum\limits_{i=1}^n\sum_{\substack{j = 1\\ j \ne i}}^n y_i y_j w_{ij} - \displaystyle\sum\limits_{i=1}^n x_i y_i + \frac{1}{\lambda} \displaystyle\sum\limits_{i=1}^n \sum_{\substack{j = 1\\ j \ne i}}^n w_{ij} g_{ri} \int_{0}^{y_i} a^{-1}(y) dy$$
这里λ是增益参数,gri是输入电导。
玻尔兹曼机
这些是具有递归结构的随机学习过程,是ANN中使用的早期优化技术的基础。Boltzmann机由Geoffrey Hinton和Terry Sejnowski于1985年发明。Hinton关于Boltzmann机的论述可以使我们更加清晰地理解。
“这个网络的一个令人惊讶的特点是它只使用局部可用的信息。权重的变化只取决于它连接的两个单元的行为,即使变化优化的是全局度量” - Ackley, Hinton 1985。
关于Boltzmann机的一些重要要点:
它们使用递归结构。
它们由随机神经元组成,这些神经元具有两种可能状态之一,即1或0。
其中一些神经元是自适应的(自由状态),而另一些神经元是固定的(冻结状态)。
如果我们将模拟退火应用于离散Hopfield网络,那么它将成为Boltzmann机。
Boltzmann机的目标
Boltzmann机的主要目的是优化问题的解决方案。Boltzmann机的工作是优化权重以及与该特定问题相关的数量。
架构
下图显示了Boltzmann机的架构。从图中可以清楚地看出,它是一个二维单元阵列。这里,单元之间互连上的权重为–p,其中p > 0。自连接的权重由b给出,其中b > 0。
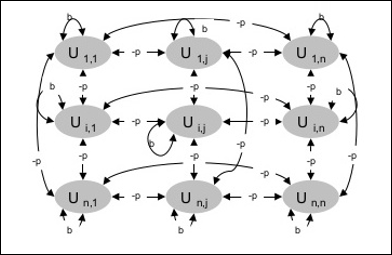
训练算法
众所周知,Boltzmann机具有固定权重,因此不需要训练算法,因为我们不需要更新网络中的权重。但是,为了测试网络,我们必须设置权重以及找到一致性函数(CF)。
Boltzmann机有一组单元Ui和Uj,并在其上具有双向连接。
我们考虑固定权重,例如wij。
如果Ui和Uj连接,则wij ≠ 0。
加权互连中也存在对称性,即wij = wji。
wii也存在,即单元之间存在自连接。
对于任何单元Ui,其状态ui将为1或0。
Boltzmann机的主要目标是最大化一致性函数(CF),这可以通过以下关系给出
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
现在,当状态从1变为0或从0变为1时,一致性的变化可以通过以下关系给出:
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
这里ui是Ui的当前状态。
系数(1 - 2ui)的变化由以下关系给出:
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:is\:currently\:off\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
通常,单元Ui不会改变其状态,但如果改变,则信息将驻留在单元本地。随着这种变化,网络的一致性也会增加。
网络接受单元状态变化的概率由以下关系给出:
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
这里,T 是控制参数。当 CF 达到最大值时,它会减小。
测试算法
步骤1 − 初始化以下内容以开始训练:
- 表示问题约束的权重
- 控制参数 T
步骤 2 − 当停止条件不满足时,继续步骤 3-8。
步骤 3 − 执行步骤 4-7。
步骤 4 − 假设其中一个状态改变了权重,并随机选择整数I, J,其值介于1 和 n 之间。
步骤 5 − 计算一致性变化如下:
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
步骤 6 − 计算该网络接受状态变化的概率
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
步骤 7 − 如下接受或拒绝此更改:
情况一 − 如果 R < AF,则接受更改。
情况二 − 如果 R ≥ AF,则拒绝更改。
这里,R 是介于 0 和 1 之间的随机数。
步骤 8 − 如下减少控制参数(温度):
T(新) = 0.95T(旧)
步骤 9 − 测试停止条件,这些条件可能是:
- 温度达到指定值
- 在指定的迭代次数内没有状态变化
盒中脑状态网络
盒中脑状态 (BSB) 神经网络是一个非线性自关联神经网络,可以扩展到具有两层或更多层的异关联。它也类似于 Hopfield 网络。它由 J.A. Anderson、J.W. Silverstein、S.A. Ritz 和 R.S. Jones 于 1977 年提出。
关于 BSB 网络的一些重要要点:
它是一个完全连接的网络,节点的最大数量取决于输入空间的维数n。
所有神经元同时更新。
神经元取值范围为 -1 到 +1。
数学公式
BSB 网络中使用的节点函数是斜坡函数,可以定义如下:
$$f(net)\:=\:min(1,\:max(-1,\:net))$$
此斜坡函数是有界且连续的。
众所周知,每个节点都会改变其状态,这可以通过以下数学关系来实现:
$$x_{t}(t\:+\:1)\:=\:f\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{i,j}x_{j}(t)\end{array}\right)$$
这里,xi(t) 是ith 节点在时间t 的状态。
从ith 节点到jth 节点的权重可以用以下关系来衡量:
$$w_{ij}\:=\:\frac{1}{P}\displaystyle\sum\limits_{p=1}^P (v_{p,i}\:v_{p,j})$$
这里,P 是训练模式的数量,这些模式是双极的。
使用Hopfield网络进行优化
优化是使设计、情况、资源和系统等尽可能有效的一种行为。利用代价函数和能量函数之间的相似性,我们可以使用高度互连的神经元来解决优化问题。这种神经网络是 Hopfield 网络,它由单层组成,包含一个或多个完全连接的循环神经元。这可用于优化。
使用 Hopfield 网络进行优化时需要注意的几点:
能量函数必须是网络的最小值。
它将找到令人满意的解决方案,而不是从存储的模式中选择一个。
Hopfield 网络找到的解决方案的质量在很大程度上取决于网络的初始状态。
旅行商问题
寻找旅行商旅行的最短路线是可以通过使用 Hopfield 神经网络进行优化的计算问题之一。
TSP 的基本概念
旅行商问题 (TSP) 是一种经典的优化问题,其中一名销售人员必须前往n 个相互连接的城市,同时保持成本和行驶距离最小。例如,销售人员必须前往一组 4 个城市 A、B、C、D,目标是找到最短的环形路线 A-B-C-D,以最大限度地降低成本,其中还包括从最后一个城市 D 到第一个城市 A 的旅行成本。
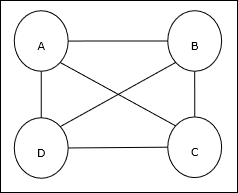
矩阵表示
实际上,n 城市 TSP 的每个路线都可以表示为n × n 矩阵,其ith 行描述ith 城市的位置。对于 4 个城市 A、B、C、D,该矩阵M 可以表示如下:
$$M = \begin{bmatrix}A: & 1 & 0 & 0 & 0 \\B: & 0 & 1 & 0 & 0 \\C: & 0 & 0 & 1 & 0 \\D: & 0 & 0 & 0 & 1 \end{bmatrix}$$
Hopfield 网络的解决方案
在考虑 Hopfield 网络对此 TSP 的解决方案时,网络中的每个节点都对应于矩阵中的一个元素。
能量函数计算
为了成为优化的解决方案,能量函数必须最小。基于以下约束,我们可以计算能量函数如下:
约束 I
第一个约束,我们将根据它计算能量函数,是矩阵M 的每一行中必须有一个元素等于 1,而每一行中的其他元素必须等于0,因为每个城市在 TSP 路线中只能出现一个位置。此约束可以用数学方式写成如下:
$$\displaystyle\sum\limits_{j=1}^n M_{x,j}\:=\:1\:for \: x\:\in \:\lbrace1,...,n\rbrace$$
现在,基于上述约束要最小化的能量函数将包含一个与以下成比例的项:
$$\displaystyle\sum\limits_{x=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{j=1}^n M_{x,j}\end{array}\right)^2$$
约束 II
众所周知,在 TSP 中,一个城市可以出现在路线中的任何位置,因此在矩阵M 的每一列中,必须有一个元素等于 1,而其他元素必须等于 0。此约束可以用数学方式写成如下:
$$\displaystyle\sum\limits_{x=1}^n M_{x,j}\:=\:1\:for \: j\:\in \:\lbrace1,...,n\rbrace$$
现在,基于上述约束要最小化的能量函数将包含一个与以下成比例的项:
$$\displaystyle\sum\limits_{j=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x=1}^n M_{x,j}\end{array}\right)^2$$
成本函数计算
假设一个用C 表示的 (n × n) 方阵表示n 个城市(其中n > 0)的 TSP 成本矩阵。计算成本函数时,以下是一些参数:
Cx, y − 成本矩阵的元素表示从城市x 到y 的旅行成本。
A 和 B 的元素的邻接性可以用以下关系表示:
$$M_{x,i}\:=\:1\:\: and\:\: M_{y,i\pm 1}\:=\:1$$
众所周知,在矩阵中,每个节点的输出值可以是 0 或 1,因此对于每对城市 A、B,我们可以将以下项添加到能量函数中:
$$\displaystyle\sum\limits_{i=1}^n C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})$$
基于上述成本函数和约束值,最终能量函数E 可以表示为:
$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{x}\displaystyle\sum\limits_{y\neq x}C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})\:+$$
$$\:\begin{bmatrix}\gamma_{1} \displaystyle\sum\limits_{x} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{i} M_{x,i}\end{array}\right)^2\:+\: \gamma_{2} \displaystyle\sum\limits_{i} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x} M_{x,i}\end{array}\right)^2 \end{bmatrix}$$
这里,γ1 和γ2 是两个加权常数。
其他优化技术
迭代梯度下降法
梯度下降,也称为最速下降,是一种迭代优化算法,用于查找函数的局部最小值。在最小化函数时,我们关注的是要最小化的成本或误差(记住旅行商问题)。它广泛用于深度学习,这在各种情况下都非常有用。这里要记住的是,我们关注的是局部优化,而不是全局优化。
主要工作原理
我们可以通过以下步骤了解梯度下降的主要工作原理:
首先,从解决方案的初始猜测开始。
然后,取该点的函数梯度。
之后,通过在梯度的负方向上逐步调整解决方案来重复此过程。
通过遵循上述步骤,算法最终将收敛到梯度为零的位置。
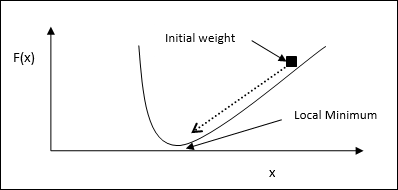
数学概念
假设我们有一个函数f(x),我们试图找到这个函数的最小值。以下是查找f(x) 最小值的步骤。
首先,为 x 给出一些初始值 $x_{0}$
现在取函数的梯度 $\nabla f$,其直觉是梯度将给出该 x 处曲线的斜率,其方向将指向函数的增加,以找出最小化它的最佳方向。
现在更改 x 如下:
$$x_{n\:+\:1}\:=\:x_{n}\:-\:\theta \nabla f(x_{n})$$
这里,θ > 0 是训练率(步长),它迫使算法采取小跳跃。
估计步长
实际上,错误的步长θ 可能无法达到收敛,因此仔细选择步长非常重要。选择步长时必须记住以下几点
不要选择太大的步长,否则会产生负面影响,即它会发散而不是收敛。
不要选择太小的步长,否则它会花费大量时间才能收敛。
关于选择步长的一些选项:
一种选择是选择固定的步长。
另一种选择是为每次迭代选择不同的步长。
模拟退火
模拟退火 (SA) 的基本概念源于固体中的退火。在退火过程中,如果我们将金属加热到其熔点以上并冷却下来,则结构特性将取决于冷却速度。我们也可以说 SA 模拟了退火冶金过程。
在 ANN 中的使用
SA 是一种随机计算方法,其灵感来自退火比拟,用于逼近给定函数的全局优化。我们可以使用 SA 来训练前馈神经网络。
算法
步骤 1 − 生成随机解决方案。
步骤 2 − 使用某个成本函数计算其成本。
步骤 3 − 生成随机相邻解决方案。
步骤 4 − 使用相同的成本函数计算新解决方案成本。
步骤 5 − 如下比较新解决方案的成本与旧解决方案的成本:
如果新解决方案成本 < 旧解决方案成本,则转到新解决方案。
步骤 6 − 测试停止条件,这可能是达到最大迭代次数或获得可接受的解决方案。
人工神经网络 - 遗传算法
自然界一直是全人类灵感的重要源泉。遗传算法 (GA) 是基于自然选择和遗传概念的搜索算法。遗传算法是进化计算这个更大计算分支的一个子集。
遗传算法由 John Holland 及其在密歇根大学的学生和同事(最著名的是 David E. Goldberg)开发,此后已在各种优化问题上进行了尝试,并取得了高度的成功。
在遗传算法中,我们有一组或一个种群的可能解来解决给定的问题。然后,这些解会进行重组和变异(就像在自然遗传中一样),产生新的后代,并且该过程在各个世代中重复。每个个体(或候选解)都被赋予一个适应度值(基于其目标函数值),适应度较高的个体有更高的机会交配并产生更“适应”的个体。这与达尔文的“适者生存”理论相符。
通过这种方式,我们不断进化出更好的个体或解决方案,直到达到停止标准。
遗传算法本质上是足够随机的,但是它们比随机局部搜索(我们只是尝试各种随机解决方案,并跟踪到目前为止最好的解决方案)的性能要好得多,因为它们也利用了历史信息。
遗传算法的优点
遗传算法具有多种优点,使其广受欢迎。这些包括:
不需要任何导数信息(对于许多现实世界的问题可能不可用)。
与传统方法相比,速度更快,效率更高。
具有非常好的并行能力。
可以优化连续函数和离散函数以及多目标问题。
提供一系列“良好”的解决方案,而不仅仅是一个解决方案。
始终可以得到问题的答案,并且随着时间的推移答案会越来越好。
当搜索空间非常大并且涉及大量参数时非常有用。
遗传算法的局限性
与任何技术一样,遗传算法也有一些局限性。这些包括:
遗传算法不适用于所有问题,特别是那些简单且可以使用导数信息的问题。
适应度值会被重复计算,这对于某些问题来说可能计算成本很高。
由于其随机性,无法保证解决方案的最优性或质量。
如果实现不当,遗传算法可能无法收敛到最优解。
遗传算法——动机
遗传算法能够“足够快”地提供“足够好”的解决方案。这使得遗传算法在解决优化问题方面具有吸引力。需要遗传算法的原因如下:
解决难题
在计算机科学中,有一大类问题是NP-Hard的。这实际上意味着,即使是最强大的计算系统也需要很长时间(甚至数年!)才能解决该问题。在这种情况下,遗传算法被证明是提供可用的近似最优解的有效工具。
基于梯度的方法的失败
传统的基于微积分的方法的工作原理是从一个随机点开始,沿着梯度的方向移动,直到到达山顶。这种技术效率很高,并且非常适用于单峰目标函数,例如线性回归中的成本函数。但是,在大多数现实世界的情况下,我们面临一个非常复杂的问题,称为景观,由许多峰和许多谷组成,这会导致此类方法失败,因为它们具有固有的陷入局部最优的倾向,如下图所示。
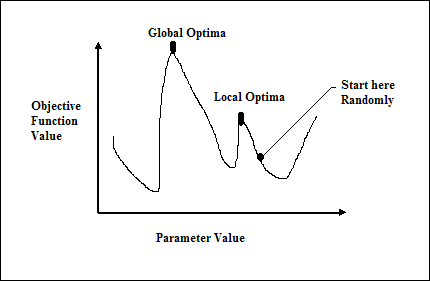
快速获得良好的解决方案
旅行商问题 (TSP) 等一些难题具有现实世界的应用,例如路径查找和 VLSI 设计。现在假设您正在使用 GPS 导航系统,并且它需要几分钟(甚至几小时)才能计算出从起点到目的地的“最佳”路径。这种现实世界应用中的延迟是不可接受的,因此需要“足够好”且“快速”交付的解决方案。
如何将遗传算法用于优化问题?
我们已经知道,优化是使设计、情况、资源和系统尽可能有效的一种行为。优化过程如下图所示。

用于优化过程的遗传算法机制的阶段
以下是将遗传算法用于问题优化时的阶段。
随机生成初始种群。
选择具有最佳适应度值的初始解。
使用变异和交叉算子重组所选解。
将后代插入种群。
现在,如果满足停止条件,则返回具有最佳适应度值的解。否则,转到步骤 2。
神经网络的应用
在研究 ANN 被广泛使用的领域之前,我们需要了解为什么 ANN 会成为首选的应用。
为什么选择人工神经网络?
我们需要通过人类的例子来理解上述问题的答案。孩提时代,我们依靠长辈(包括父母或老师)的帮助来学习。然后,通过自学或练习,我们终身学习。科学家和研究人员也正在使机器像人类一样变得智能,而 ANN 正因以下原因在其中发挥着非常重要的作用:
借助神经网络,我们可以找到那些算法方法成本过高或不存在的问题的解决方案。
神经网络可以通过示例学习,因此我们不需要对其进行太多编程。
神经网络的精度和速度比传统速度显著提高。
应用领域
以下是 ANN 正在使用的一些领域。这表明 ANN 在其发展和应用中具有跨学科的方法。
语音识别
语音在人际互动中占据突出地位。因此,人们自然希望计算机具有语音界面。在当今时代,为了与机器进行通信,人类仍然需要复杂的语言,这些语言难以学习和使用。为了减轻这种沟通障碍,一个简单的解决方案可能是使用机器能够理解的口语进行沟通。
这一领域已经取得了长足的进步,但是,此类系统仍然面临词汇量或语法有限的问题,以及在不同条件下为不同的说话者重新训练系统的问题。ANN 在这个领域发挥着重要作用。以下 ANN 已用于语音识别:
多层网络
具有递归连接的多层网络
Kohonen 自组织特征映射
最实用的网络是 Kohonen 自组织特征映射,其输入是语音波形的短片段。它将把相同类型的音素映射到输出数组,称为特征提取技术。提取特征后,借助一些声学模型作为后端处理,它将识别话语。
字符识别
这是一个有趣的问题,属于模式识别的一般领域。许多神经网络已被开发用于自动识别手写字符,无论是字母还是数字。以下是已用于字符识别的一些 ANN:
- 多层神经网络,例如反向传播神经网络。
- Neocognitron
尽管反向传播神经网络具有多个隐藏层,但从一层到下一层的连接模式是局部的。类似地,neocognitron 也具有多个隐藏层,其训练是针对此类应用逐层进行的。
签名验证应用
签名是在法律交易中授权和验证人员的最有用方法之一。签名验证技术是一种非视觉技术。
对于此应用,第一种方法是提取特征,或者更确切地说,是表示签名的几何特征集。使用这些特征集,我们必须使用高效的神经网络算法训练神经网络。在验证阶段,这个训练好的神经网络将把签名分类为真实或伪造。
人脸识别
这是识别给定面部的生物识别方法之一。由于“非面部”图像的特征,这是一项典型的任务。但是,如果神经网络经过良好训练,则可以将其分为两类:具有面部的图像和不具有面部的图像。
首先,必须预处理所有输入图像。然后,必须降低该图像的维数。最后,必须使用神经网络训练算法对其进行分类。以下神经网络用于使用预处理图像进行训练:
使用反向传播算法训练的全连接多层前馈神经网络。
对于降维,使用主成分分析 (PCA)。