
玻尔兹曼机
这些是具有递归结构的随机学习过程,是ANN早期优化技术的基础。玻尔兹曼机由Geoffrey Hinton和Terry Sejnowski于1985年发明。Hinton对玻尔兹曼机的论述可以提供更清晰的理解。
“这个网络的一个令人惊讶的特点是它只使用局部可用的信息。权重的变化只取决于它连接的两个单元的行为,即使这种变化优化的是一个全局度量” - Ackley, Hinton 1985。
关于玻尔兹曼机的一些重要点:
它们使用递归结构。
它们由随机神经元组成,这些神经元具有两种可能的状态之一,即1或0。
其中一些神经元是自适应的(自由状态),而另一些则被钳制(冻结状态)。
如果我们对离散Hopfield网络应用模拟退火,它就会变成玻尔兹曼机。
玻尔兹曼机的目标
玻尔兹曼机的主要目的是优化问题的解决方案。玻尔兹曼机的工作是优化与特定问题相关的权重和数量。
架构
下图显示了玻尔兹曼机的架构。从图中可以清楚地看出,它是一个二维单元阵列。这里,单元之间互连上的权重为–p,其中p > 0。自连接的权重由b给出,其中b > 0。
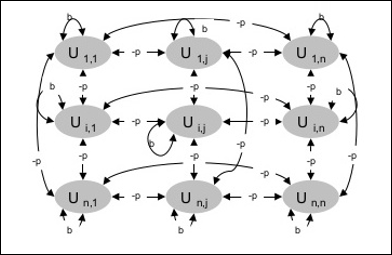
训练算法
众所周知,玻尔兹曼机具有固定的权重,因此不需要训练算法,因为我们不需要更新网络中的权重。但是,要测试网络,我们必须设置权重以及找到共识函数 (CF)。
玻尔兹曼机有一组单元Ui和Uj,并且在它们之间具有双向连接。
我们考虑固定权重,例如wij。
如果Ui和Uj连接,则wij ≠ 0。
加权互连中也存在对称性,即wij = wji。
wii也存在,即单元之间存在自连接。
对于任何单元Ui,其状态ui为1或0。
玻尔兹曼机的主要目标是最大化共识函数 (CF),其关系如下所示
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
现在,当状态从1变为0或从0变为1时,共识的变化可以通过以下关系给出:
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
这里ui是Ui的当前状态。
系数 (1 - 2ui) 的变化由以下关系给出:
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:当前处于关闭状态\\-1, & U_{i}\:当前处于开启状态\end{cases}$$
通常,单元Ui不会改变其状态,但如果改变,则信息将驻留在单元的本地。随着这种变化,网络的共识也会增加。
网络接受单元状态变化的概率由以下关系给出:
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
这里,T是控制参数。当CF达到最大值时,它会减小。
测试算法
步骤1 - 初始化以下内容以开始训练:
- 表示问题约束的权重
- 控制参数T
步骤2 - 当停止条件不为真时,继续步骤3-8。
步骤3 - 执行步骤4-7。
步骤4 - 假设其中一个状态改变了权重,并将整数I, J选择为1和n之间的随机值。
步骤5 - 计算共识变化如下:
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
步骤6 - 计算网络接受状态变化的概率
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
步骤7 - 接受或拒绝此更改,如下所示:
情况一 - 如果R < AF,则接受更改。
情况二 - 如果R ≥ AF,则拒绝更改。
这里,R是0到1之间的随机数。
步骤8 - 按如下方式减少控制参数(温度):
T(new) = 0.95T(old)
步骤9 - 测试停止条件,例如:
- 温度达到指定值
- 在指定的迭代次数内没有状态变化