
人工神经网络 - 构建模块
ANN 的处理取决于以下三个构建模块:
- 网络拓扑结构
- 权重的调整或学习
- 激活函数
在本章中,我们将详细讨论 ANN 的这三个构建模块。
网络拓扑结构
网络拓扑结构是指网络的排列方式,以及其节点和连接线。根据拓扑结构,ANN 可以分为以下几种类型:
前馈网络
它是一个非递归网络,其处理单元/节点分层排列,每一层中的所有节点都与前一层的节点连接。连接具有不同的权重。没有反馈回路,这意味着信号只能单向流动,从输入到输出。它可以分为以下两种类型:
单层前馈网络 - 该概念是指只有一个加权层的 ANN。换句话说,我们可以说输入层与输出层完全连接。
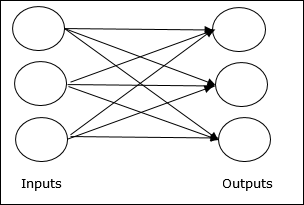
多层前馈网络 - 该概念是指具有多个加权层的 ANN。由于该网络在输入层和输出层之间有一个或多个层,因此称为隐藏层。
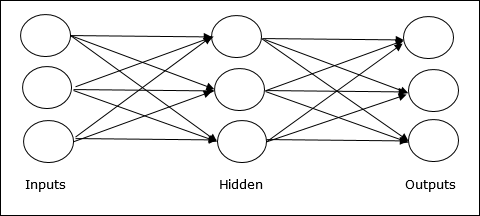
反馈网络
顾名思义,反馈网络具有反馈路径,这意味着信号可以通过回路双向流动。这使得它成为一个非线性动态系统,该系统会持续变化,直到达到平衡状态。它可以分为以下几种类型:
递归网络 - 它们是具有闭环的反馈网络。以下是两种类型的递归网络。
完全递归网络 - 它是最简单的 ANN 架构,因为所有节点都连接到所有其他节点,并且每个节点都充当输入和输出。
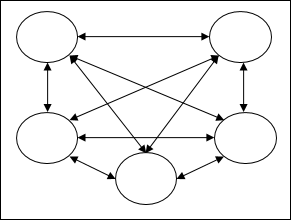
Jordan 网络 - 它是一个闭环网络,其中输出将再次作为反馈返回到输入,如下面的图所示。
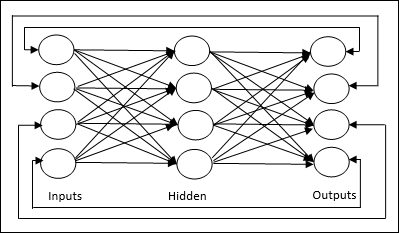
权重的调整或学习
在人工神经网络中,学习是指修改指定网络中神经元之间连接权重的方法。ANN 中的学习可以分为三类:监督学习、无监督学习和强化学习。
监督学习
顾名思义,这种类型的学习是在教师的监督下进行的。此学习过程是依赖性的。
在监督学习下训练 ANN 期间,将输入向量呈现给网络,网络将输出一个输出向量。将此输出向量与所需的输出向量进行比较。如果实际输出与所需输出向量之间存在差异,则会生成一个误差信号。根据此误差信号,调整权重,直到实际输出与所需输出匹配。
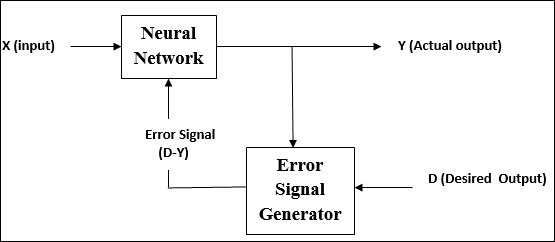
无监督学习
顾名思义,这种类型的学习是在没有教师监督的情况下进行的。此学习过程是独立的。
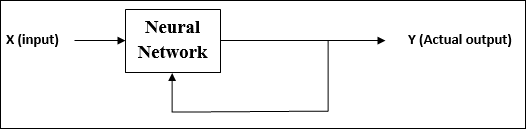
在无监督学习下训练 ANN 期间,将相似类型的输入向量组合成集群。当应用新的输入模式时,神经网络将给出输出响应,指示输入模式所属的类别。
没有来自环境的反馈,说明所需输出是什么以及它是否正确。因此,在这种类型的学习中,网络本身必须从输入数据中发现模式和特征,以及输入数据与输出之间的关系。
强化学习
顾名思义,这种类型的学习用于增强或加强网络对某些评论信息。此学习过程类似于监督学习,但是我们可能的信息非常少。
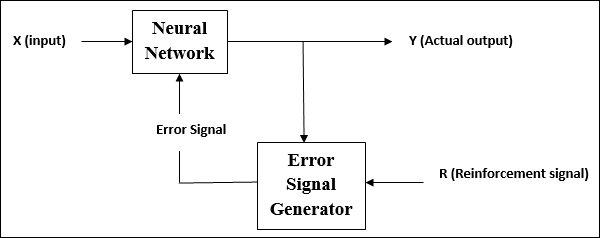
在强化学习下训练网络期间,网络会从环境中接收一些反馈。这使得它有点类似于监督学习。但是,此处获得的反馈是评价性的,而不是指导性的,这意味着与监督学习不同,这里没有教师。在接收反馈后,网络会调整权重以在将来获得更好的评论信息。
激活函数
它可以定义为对输入施加的额外力量或努力以获得精确的输出。在 ANN 中,我们还可以对输入应用激活函数以获得精确的输出。以下是我们感兴趣的一些激活函数:
线性激活函数
它也称为恒等函数,因为它不执行任何输入编辑。它可以定义为:
$$F(x)\:=\:x$$
Sigmoid 激活函数
它有两种类型,如下所示:
二进制 sigmoid 函数 - 此激活函数执行 0 到 1 之间的输入编辑。它是正向的。它始终是有界的,这意味着其输出不能小于 0 且大于 1。它也是严格递增的,这意味着输入越多,输出越高。它可以定义为
$$F(x)\:=\:sigm(x)\:=\:\frac{1}{1\:+\:exp(-x)}$$
双极 sigmoid 函数 - 此激活函数执行 -1 到 1 之间的输入编辑。它可以是正的或负的。它始终是有界的,这意味着其输出不能小于 -1 且大于 1。它也像 sigmoid 函数一样严格递增。它可以定义为
$$F(x)\:=\:sigm(x)\:=\:\frac{2}{1\:+\:exp(-x)}\:-\:1\:=\:\frac{1\:-\:exp(x)}{1\:+\:exp(x)}$$