
人工神经网络 - Hopfield 网络
Hopfield 神经网络由 John J. Hopfield 博士于 1982 年发明。它由一个包含一个或多个完全连接的循环神经元的单层组成。Hopfield 网络通常用于自动关联和优化任务。
离散 Hopfield 网络
一种以离散方式运行的 Hopfield 网络,换句话说,可以认为输入和输出模式是离散向量,其本质上可以是二进制 (0,1) 或双极性 (+1, -1)。该网络具有对称权重,没有自连接,即 wij = wji 和 wii = 0。
架构
以下是一些关于离散 Hopfield 网络需要注意的重要事项:
该模型由具有一个反相输出和一个非反相输出的神经元组成。
每个神经元的输出应该是其他神经元的输入,但不能是自身的输入。
权重/连接强度由 wij 表示。
连接可以是兴奋性的,也可以是抑制性的。如果神经元的输出与输入相同,则为兴奋性,否则为抑制性。
权重应该是对称的,即 wij = wji
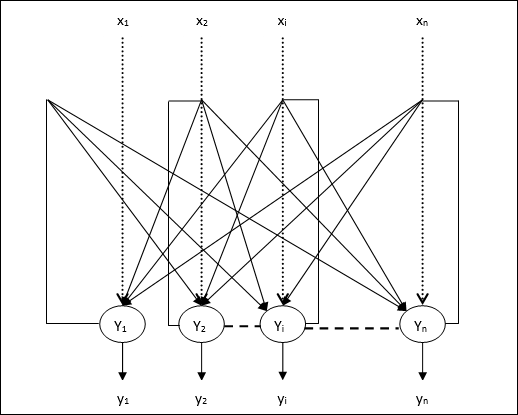
从 Y1 到 Y2、Yi 和 Yn 的输出分别具有权重 w12、w1i 和 w1n。类似地,其他弧线在其上也有权重。
训练算法
在离散 Hopfield 网络的训练过程中,权重将被更新。众所周知,我们可以拥有二进制输入向量以及双极性输入向量。因此,在这两种情况下,都可以使用以下关系更新权重
情况 1 - 二进制输入模式
对于一组二进制模式 s(p), p = 1 到 P
这里,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
权重矩阵由下式给出
$$w_{ij}\:=\:\sum_{p=1}^P[2s_{i}(p)-\:1][2s_{j}(p)-\:1]\:\:\:\:\:for\:i\:\neq\:j$$
情况 2 - 双极性输入模式
对于一组二进制模式 s(p), p = 1 到 P
这里,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
权重矩阵由下式给出
$$w_{ij}\:=\:\sum_{p=1}^P[s_{i}(p)][s_{j}(p)]\:\:\:\:\:for\:i\:\neq\:j$$
测试算法
步骤 1 - 初始化权重,这些权重是使用 Hebbian 原理通过训练算法获得的。
步骤 2 - 如果网络的激活未得到巩固,则执行步骤 3-9。
步骤 3 - 对于每个输入向量 X,执行步骤 4-8。
步骤 4 - 使网络的初始激活等于外部输入向量 X,如下所示:
$$y_{i}\:=\:x_{i}\:\:\:for\:i\:=\:1\:to\:n$$
步骤 5 - 对于每个单元 Yi,执行步骤 6-9。
步骤 6 - 计算网络的净输入,如下所示:
$$y_{ini}\:=\:x_{i}\:+\:\displaystyle\sum\limits_{j}y_{j}w_{ji}$$
步骤 7 - 对净输入应用以下激活以计算输出:
$$y_{i}\:=\begin{cases}1 & if\:y_{ini}\:>\:\theta_{i}\\y_{i} & if\:y_{ini}\:=\:\theta_{i}\\0 & if\:y_{ini}\:<\:\theta_{i}\end{cases}$$
这里 $\theta_{i}$ 是阈值。
步骤 8 - 将此输出 yi 广播到所有其他单元。
步骤 9 - 测试网络的连接。
能量函数评估
能量函数定义为系统状态的有界且非增函数。
能量函数 Ef,也称为 Lyapunov 函数,确定离散 Hopfield 网络的稳定性,其特征如下:
$$E_{f}\:=\:-\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^n y_{i}y_{j}w_{ij}\:-\:\displaystyle\sum\limits_{i=1}^n x_{i}y_{i}\:+\:\displaystyle\sum\limits_{i=1}^n \theta_{i}y_{i}$$
条件 - 在稳定网络中,只要节点状态发生变化,上述能量函数就会降低。
假设当节点 i 的状态从 $y_i^{(k)}$ 更改为 $y_i^{(k\:+\:1)}$ 时,能量变化 $\Delta E_{f}$ 由以下关系给出
$$\Delta E_{f}\:=\:E_{f}(y_i^{(k+1)})\:-\:E_{f}(y_i^{(k)})$$
$$=\:-\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{ij}y_i^{(k)}\:+\:x_{i}\:-\:\theta_{i}\end{array}\right)(y_i^{(k+1)}\:-\:y_i^{(k)})$$
$$=\:-\:(net_{i})\Delta y_{i}$$
这里 $\Delta y_{i}\:=\:y_i^{(k\:+\:1)}\:-\:y_i^{(k)}$
能量的变化取决于一次只能更新一个单元的激活这一事实。
连续 Hopfield 网络
与离散 Hopfield 网络相比,连续网络将时间视为连续变量。它也用于自动关联和优化问题,例如旅行商问题。
模型 - 可以通过添加电子元件(例如放大器)来构建模型或架构,这些放大器可以通过 S 型激活函数将输入电压映射到输出电压。
能量函数评估
$$E_f = \frac{1}{2}\displaystyle\sum\limits_{i=1}^n\sum_{\substack{j = 1\\ j \ne i}}^n y_i y_j w_{ij} - \displaystyle\sum\limits_{i=1}^n x_i y_i + \frac{1}{\lambda} \displaystyle\sum\limits_{i=1}^n \sum_{\substack{j = 1\\ j \ne i}}^n w_{ij} g_{ri} \int_{0}^{y_i} a^{-1}(y) dy$$
这里 λ 是增益参数,gri 是输入电导。