
神经网络优化技术
迭代梯度下降技术
梯度下降,也称为最速下降,是一种迭代优化算法,用于寻找函数的局部最小值。在最小化函数时,我们关注的是要最小化的成本或误差(记住旅行商问题)。它广泛用于深度学习,这在各种情况下都很有用。这里需要记住的是,我们关注的是局部优化,而不是全局优化。
主要工作原理
我们可以借助以下步骤来理解梯度下降的主要工作原理:
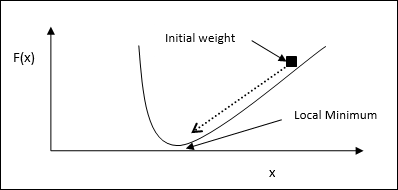
首先,从一个初始的解猜测开始。
然后,在该点计算函数的梯度。
之后,通过沿梯度的负方向移动解来重复该过程。
通过遵循上述步骤,算法最终将收敛到梯度为零的位置。
数学概念
假设我们有一个函数f(x),我们试图找到该函数的最小值。以下是找到f(x)最小值的步骤。
首先,为x赋予某个初始值$x_{0}$
现在计算函数的梯度$\nabla f$,其直觉是梯度将在该x处给出曲线的斜率,并且其方向将指向函数的增加,以找出最小化它的最佳方向。
现在按如下方式更改x:
$$x_{n\:+\:1}\:=\:x_{n}\:-\:\theta \nabla f(x_{n})$$
这里,θ > 0是训练率(步长),它迫使算法采取小步跳跃。
估计步长
实际上,错误的步长θ可能无法达到收敛,因此仔细选择步长非常重要。在选择步长时必须记住以下几点
不要选择太大的步长,否则会产生负面影响,即它会发散而不是收敛。
不要选择太小的步长,否则它需要很长时间才能收敛。
关于选择步长的一些选项:
一种选择是选择一个固定的步长。
另一种选择是为每次迭代选择不同的步长。
模拟退火
模拟退火(SA)的基本概念受到固体退火过程的启发。在退火过程中,如果我们将金属加热到其熔点以上并将其冷却下来,则结构特性将取决于冷却速率。我们也可以说SA模拟了金属退火过程。
在ANN中的使用
SA是一种随机计算方法,受退火类比的启发,用于近似给定函数的全局优化。我们可以使用SA来训练前馈神经网络。
算法
步骤1 - 生成一个随机解。
步骤2 - 使用某个成本函数计算其成本。
步骤3 - 生成一个随机的邻近解。
步骤4 - 使用相同的成本函数计算新解的成本。
步骤5 - 将新解的成本与旧解的成本进行比较,如下所示:
如果Cost新解 < Cost旧解,则移动到新解。
步骤6 - 测试停止条件,该条件可能是达到最大迭代次数或获得可接受的解。
Hopfield网络技术
Hopfield神经网络是由John J. Hopfield博士于1982年发明的。它由一个单层组成,该单层包含一个或多个完全连接的循环神经元。Hopfield网络通常用于自动关联和优化任务。
阅读更多:使用Hopfield网络进行优化