圆的弦、弦长及其定理

---

引言

弦是连接圆周上任意两点的线段。圆是欧几里得几何中众所周知的二维图形。它具有各种组成部分，包括弦、半径、直径等。在本教程中，我们将讨论圆的弦的定义、公式和一些相关定理。

圆

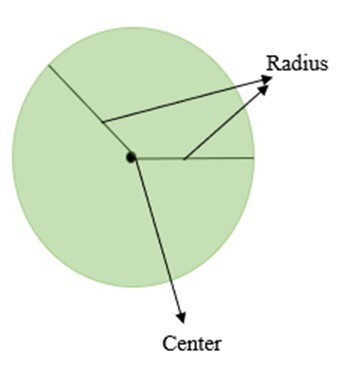
• 圆是在平面上绘制的二维图形，圆上每一点到一个固定点的距离相等。

• 该固定点称为圆心。

• 圆的尺寸用其半径表示。

• 圆心与圆上任意一点之间的距离称为半径。

• “圆”这个词来源于拉丁语“circulus”（意为小环）。圆的图形表示如下所示。

圆具有多种性质，下面简要总结。

• 圆是一个曲面，任何直线都界定了曲面区域。因此，它不属于多边形类别。

• 具有相同半径的圆被认为是全等圆。

• 任何弦的垂直平分线都经过圆心。

• 最长的弦是圆的直径。

• 连接两个圆的交点的线段垂直于连接这两个圆的圆心的线段。

• 圆可以内接于三角形或正方形。

• 在直径的端点处画出的切线彼此平行。

圆的弦

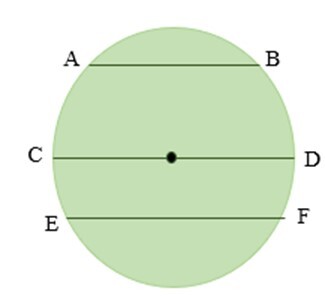
• 弦是连接圆上任意两点的线段。

• 换句话说，弦的端点位于圆周上。

• 在圆中可以画出无限多条弦。

• 线段AB、CD和EF是下图中表示的一些弦。

弦有以下几种性质。

• 直径是圆中最长的弦。

• 弦将圆分成两部分。

• 直径将圆分成两等分。

• 当弦在两侧延伸时，它被称为割线。

已知弦到圆心的距离求弦长

如果已知弦到圆心的距离，则可以使用以下公式计算弦长。

$$\mathrm{S\:=\:2\sqrt{(r^{2}\:-\:p^{2})}}$$

其中 r = 圆的半径

p = 弦到圆心的垂直距离

S = 弦长

证明 −

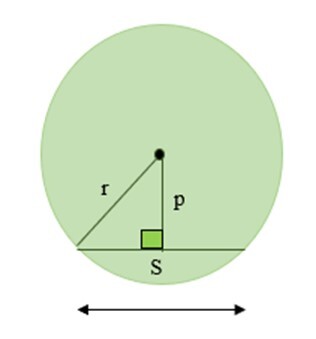
在上图中，直角三角形的斜边是圆的半径。垂直平分线是三角形的一条边。众所周知，垂直线平分弦。因此，弦长将是直角三角形底边的两倍。

现在，使用勾股定理，

$$\mathrm{底边\:=\:\sqrt{(r^{2}\:-\:p^{2})}}$$

$$\mathrm{\Longrightarrow\:弦长\:=\:2\times\:底边\:=\:2\sqrt{(r^{2}\:-\:p^{2})}}$$

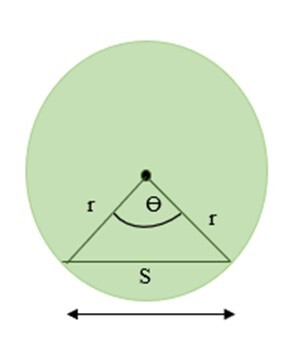
已知圆心角求弦长

让我们考虑一个半径为r、弦长为S的圆。弦在圆心处成θ角。

使用三角函数，弦长 $\mathrm{=\:2\times\:r\times\:\sin\frac{\theta}{2}}$

圆的弦定理

与弦相关的各种定理如下所述。

• 定理 1 − 从圆心到弦所作的垂线平分弦。在给定图中，TS = SM。

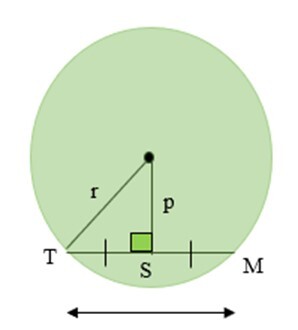
• 定理 2 − 如果从圆心到各自弦的垂线长度相等，则两条弦相等。在给定图中，TM = AB。

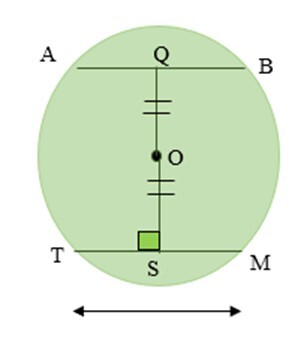
• 定理 3 − 如果两条弦在圆心处张成的角相等，则两条弦相等。

• 定理 4 − 对于两条不相等的弦，较长的一条比较短的一条更靠近圆心。

例题

1) 在给定图中，OP = 10 厘米，TS = 6 厘米。求弦 TM 的长度？

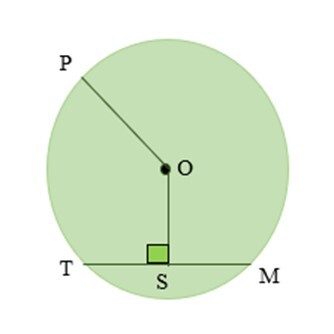
答案 −

圆的半径 $\mathrm{=\:r\:=\:OP\:=\:10\:厘米}$

直角三角形的底边 = TS = 6 厘米

使用勾股定理，

$$\mathrm{OS\:=\:\sqrt{(OP^{2}\:-\:TS^{2})}}$$

$$\mathrm{\Longrightarrow\:OS\:=\:\sqrt{(10^{2}\:-\:6^{2})}}$$

$$\mathrm{\Longrightarrow\:OS\:=\:\sqrt{64}\:=\:8\:厘米}$$

使用弦的公式，

$$\mathrm{\Longrightarrow\:弦长\:=\:2\sqrt{(半径^{2}\:-\:垂线^{2})}}$$

$$\mathrm{\Longrightarrow\:弦长\:=\:2\sqrt{(10^{2}\:-\:8^{2})}}$$

$$\mathrm{\Longrightarrow\:弦长\:=\:12\:厘米}$$

∴ 弦长为 12 厘米。

2) 如果 OT = 15 厘米且 OS = 4 厘米，求弦长和 TS。

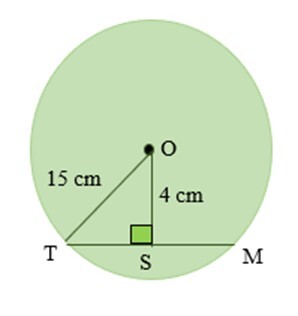
答案 −

在直角三角形 OTS 中，

$$\mathrm{OT^{2}\:=\:OS^{2}\:+\:TS^{2}}$$

$$\mathrm{\Longrightarrow\:15^{2}\:=\:4^{2}\:+\:TS^{2}}$$

$$\mathrm{\Longrightarrow\:TS^{2}\:=\:15^{2}\:-\:4^{2}}$$

$$\mathrm{\Longrightarrow\:TS^{2}\:=\:225\:-\:16\:=\:209}$$

$$\mathrm{\Longrightarrow\:TS\:=\:\sqrt{209}\:=\:14.46\:厘米}$$

弦长 $\mathrm{=\:TM\:=\:2\times\:TS\:=\:2\times\:14.46\:=\:28.92\:厘米}$

∴ 弦长和 TS 分别为 28.92 厘米和 14.46 厘米。

文字题

• 问题 1 − 如果直径长和从圆心到弦的垂线长分别为 18 厘米和 3 厘米，求弦长。

• 问题 2 − 一条弦在圆心处张成 30° 的角。圆的半径为 10 厘米。求弦长。

• 问题 3 − 圆的弦是半径的一半。求弦在圆心处张成的角。

结论

本教程简要介绍了弦及其各种性质。此外，还简要介绍了与弦长相关的基本公式。本教程中说明了与圆的弦相关的某些定理。此外，还提供了一些例题，以更好地理解这个概念。总之，本教程可能有助于理解弦及其定理的基本概念。

常见问题

1. 弦的长度可以小于圆的半径吗？

是的。弦的长度并不一定总是大于半径。

2. 在圆中可以画多少条弦？

在圆中可以画出无限多条弦。然而，直径是圆中最长的弦。

3. 弦和扇形有什么区别？

弦是连接圆周上任意两点的线段，而扇形是圆的一部分，由两条半径和一条弧组成。一个圆可以分成两个扇形，而一个圆中可以画出无限多条弦。

4. 切线可以称为弦吗？

切线是只与圆相交于一点的线段，而弦是与圆相交于两点的线段。因此，切线不能称为弦。

5. 当两条半径连接弦的两端时，会形成什么样的三角形？

如果两条半径连接弦的端点，则会形成等腰三角形。此外，从圆心到弦的垂线平分弦。