
- 模糊逻辑教程
- 模糊逻辑 - 首页
- 模糊逻辑 - 简介
- 模糊逻辑 - 经典集合论
- 模糊逻辑 - 集合论
- 模糊逻辑 -隶属函数
- 传统模糊知识回顾
- 近似推理
- 模糊逻辑 - 推理系统
- 模糊逻辑 - 数据库和查询
- 模糊逻辑 - 量化
- 模糊逻辑 - 决策
- 模糊逻辑 - 控制系统
- 自适应模糊控制器
- 神经网络中的模糊性
- 模糊逻辑 - 应用
- 模糊逻辑有用资源
- 模糊逻辑 - 快速指南
- 模糊逻辑 - 有用资源
- 模糊逻辑 - 讨论
自适应模糊控制器
在本章中,我们将讨论什么是自适应模糊控制器以及它是如何工作的。自适应模糊控制器设计了一些可调参数,以及用于调整它们的嵌入式机制。自适应控制器已被用于提高控制器的性能。
实施自适应算法的基本步骤
现在让我们讨论实施自适应算法的基本步骤。
收集可观察数据 - 收集可观察数据以计算控制器的性能。
调整控制器参数 - 现在,借助控制器性能,将计算控制器参数的调整。
提高控制器性能 - 在此步骤中,调整控制器参数以提高控制器的性能。
操作概念
控制器的设计基于一个假设的数学模型,该模型类似于实际系统。计算实际系统与其数学表示之间的误差,如果误差相对较小,则认为该模型有效。
还存在一个阈值常数,用于设定控制器有效性的边界。控制输入被馈送到实际系统和数学模型中。在这里,假设$x\left ( t \right )$是实际系统的输出,$y\left ( t \right )$是数学模型的输出。然后可以计算误差$\epsilon \left ( t \right )$如下:
$$\epsilon \left ( t \right ) = x\left ( t \right ) - y\left ( t \right )$$
这里,$x$期望值是我们希望从系统中获得的输出,$\mu \left ( t \right )$是来自控制器并同时进入实际系统和数学模型的输出。
下图显示了如何跟踪实际系统输出和数学模型输出之间的误差函数:
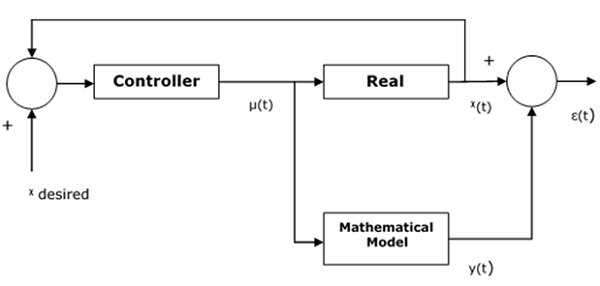
系统的参数化
基于模糊数学模型设计的模糊控制器将具有以下形式的模糊规则:
规则 1 - 如果$x_1\left ( t_n \right )\in X_{11} \: AND...AND\: x_i\left ( t_n \right )\in X_{1i}$
则$\mu _1\left ( t_n \right ) = K_{11}x_1\left ( t_n \right ) + K_{12}x_2\left ( t_n \right ) \: +...+ \: K_{1i}x_i\left ( t_n \right )$
规则 2 - 如果$x_1\left ( t_n \right )\in X_{21} \: AND...AND \: x_i\left ( t_n \right )\in X_{2i}$
则$\mu _2\left ( t_n \right ) = K_{21}x_1\left ( t_n \right ) + K_{22}x_2\left ( t_n \right ) \: +...+ \: K_{2i}x_i\left ( t_n \right ) $
.
.
.
规则 j - 如果$x_1\left ( t_n \right )\in X_{k1} \: AND...AND \: x_i\left ( t_n \right )\in X_{ki}$
则$\mu _j\left ( t_n \right ) = K_{j1}x_1\left ( t_n \right ) + K_{j2}x_2\left ( t_n \right ) \: +...+ \: K_{ji}x_i\left ( t_n \right ) $
以上参数集表征了控制器。
机制调整
调整控制器参数以提高控制器的性能。计算参数调整的过程就是调整机制。
在数学上,令$\theta ^\left ( n \right )$为在时间$t = t_n$要调整的参数集。调整可以是参数的重新计算,
$$\theta ^\left ( n \right ) = \Theta \left ( D_0,\: D_1, \: ..., \:D_n \right )$$
这里$D_n$是在时间$t = t_n$收集的数据。
现在,通过基于其先前值更新参数集来重新制定此公式,
$$\theta ^\left ( n \right ) = \phi ( \theta ^{n-1}, \: D_n)$$
选择自适应模糊控制器的参数
选择自适应模糊控制器需要考虑以下参数:
系统能否完全由模糊模型近似?
如果系统可以完全由模糊模型近似,那么这个模糊模型的参数是否很容易获得,或者必须在线确定?
如果系统不能完全由模糊模型近似,它能否由一组模糊模型分段近似?
如果系统可以由一组模糊模型近似,那么这些模型是否具有相同的格式但参数不同,或者它们是否具有不同的格式?
如果系统可以由一组具有相同格式的模糊模型近似,每个模型都有一组不同的参数,那么这些参数集是否很容易获得,或者必须在线确定?